Quantum Multiple Kernel Learning

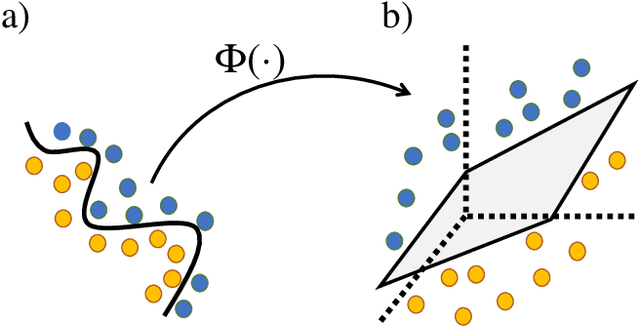
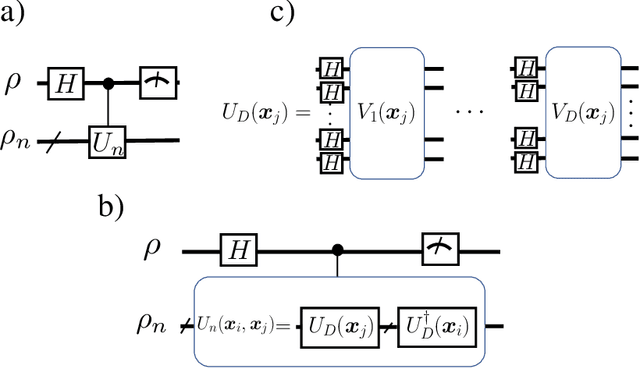
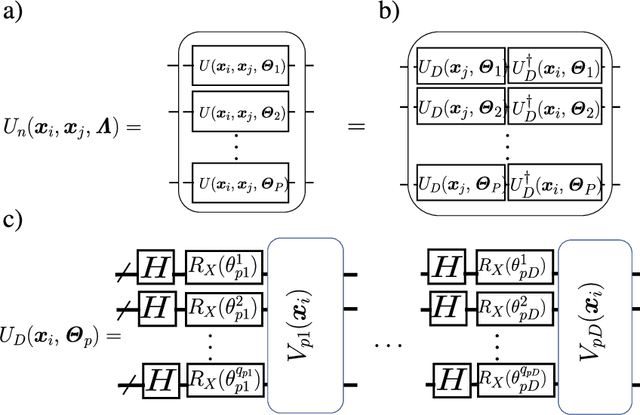
Kernel methods play an important role in machine learning applications due to their conceptual simplicity and superior performance on numerous machine learning tasks. Expressivity of a machine learning model, referring to the ability of the model to approximate complex functions, has a significant influence on its performance in these tasks. One approach to enhancing the expressivity of kernel machines is to combine multiple individual kernels to arrive at a more expressive combined kernel. This approach is referred to as multiple kernel learning (MKL). In this work, we propose an MKL method we refer to as quantum MKL, which combines multiple quantum kernels. Our method leverages the power of deterministic quantum computing with one qubit (DQC1) to estimate the combined kernel for a set of classically intractable individual quantum kernels. The combined kernel estimation is achieved without explicitly computing each individual kernel, while still allowing for the tuning of individual kernels in order to achieve better expressivity. Our simulations on two binary classification problems---one performed on a synthetic dataset and the other on a German credit dataset---demonstrate the superiority of the quantum MKL method over single quantum kernel machines.

Free energy-based reinforcement learning using a quantum processor

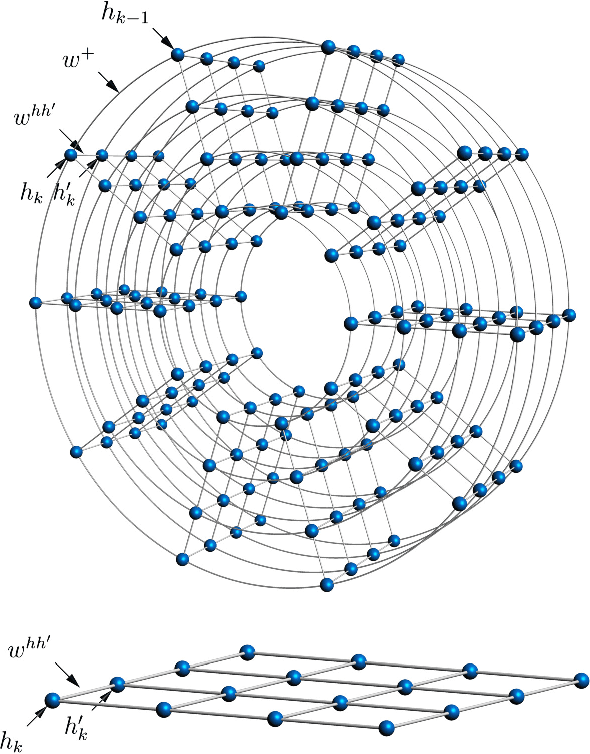
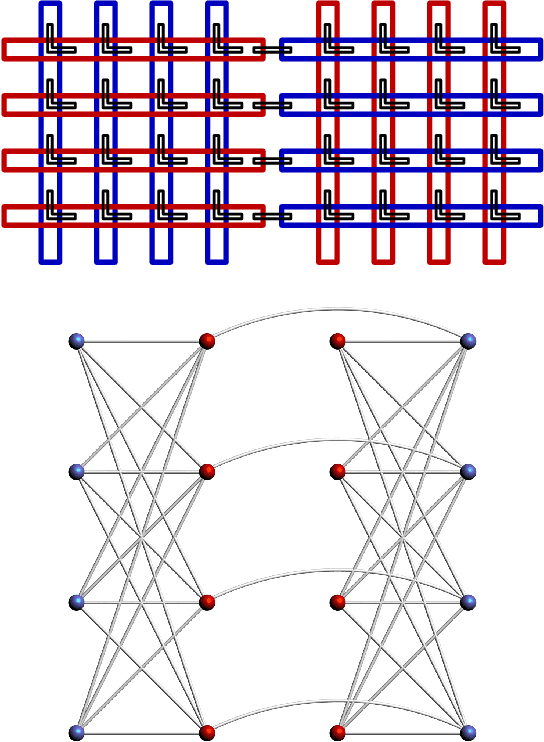
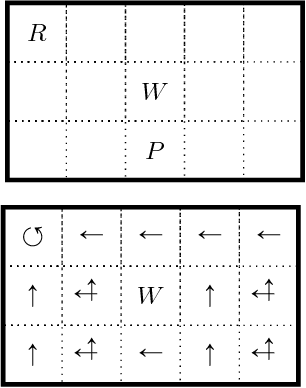
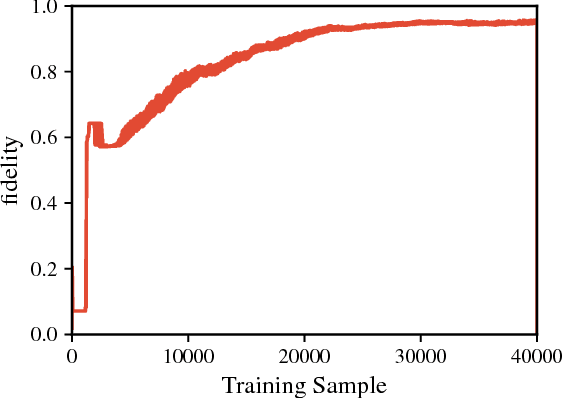
Recent theoretical and experimental results suggest the possibility of using current and near-future quantum hardware in challenging sampling tasks. In this paper, we introduce free energy-based reinforcement learning (FERL) as an application of quantum hardware. We propose a method for processing a quantum annealer's measured qubit spin configurations in approximating the free energy of a quantum Boltzmann machine (QBM). We then apply this method to perform reinforcement learning on the grid-world problem using the D-Wave 2000Q quantum annealer. The experimental results show that our technique is a promising method for harnessing the power of quantum sampling in reinforcement learning tasks.

Learning in Quantum Control: High-Dimensional Global Optimization for Noisy Quantum Dynamics

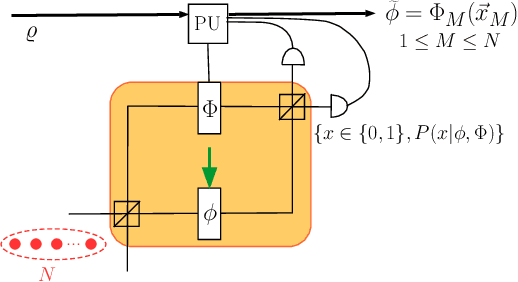
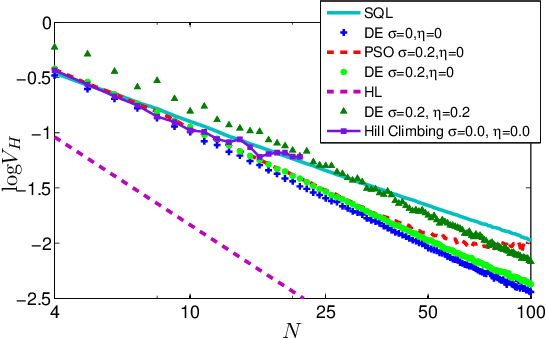
Quantum control is valuable for various quantum technologies such as high-fidelity gates for universal quantum computing, adaptive quantum-enhanced metrology, and ultra-cold atom manipulation. Although supervised machine learning and reinforcement learning are widely used for optimizing control parameters in classical systems, quantum control for parameter optimization is mainly pursued via gradient-based greedy algorithms. Although the quantum fitness landscape is often compatible with greedy algorithms, sometimes greedy algorithms yield poor results, especially for large-dimensional quantum systems. We employ differential evolution algorithms to circumvent the stagnation problem of non-convex optimization. We improve quantum control fidelity for noisy system by averaging over the objective function. To reduce computational cost, we introduce heuristics for early termination of runs and for adaptive selection of search subspaces. Our implementation is massively parallel and vectorized to reduce run time even further. We demonstrate our methods with two examples, namely quantum phase estimation and quantum gate design, for which we achieve superior fidelity and scalability than obtained using greedy algorithms.

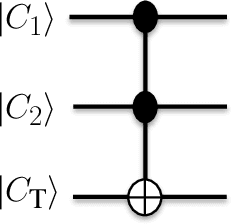
Designing High-Fidelity Single-Shot Three-Qubit Gates: A Machine Learning Approach

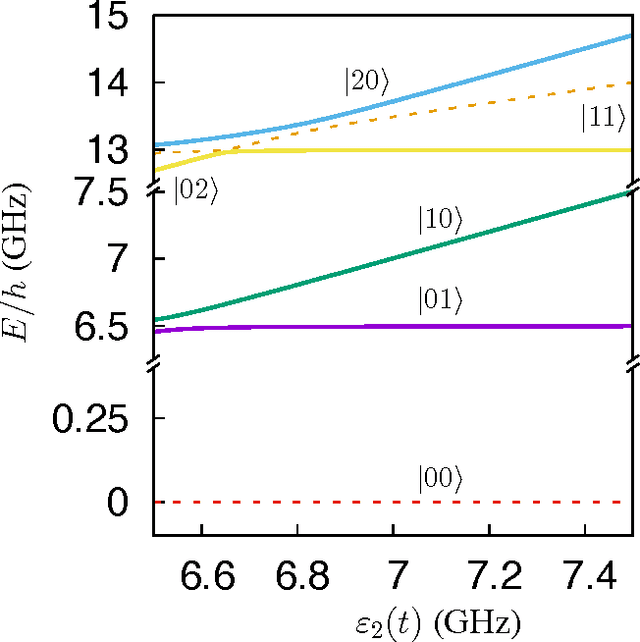
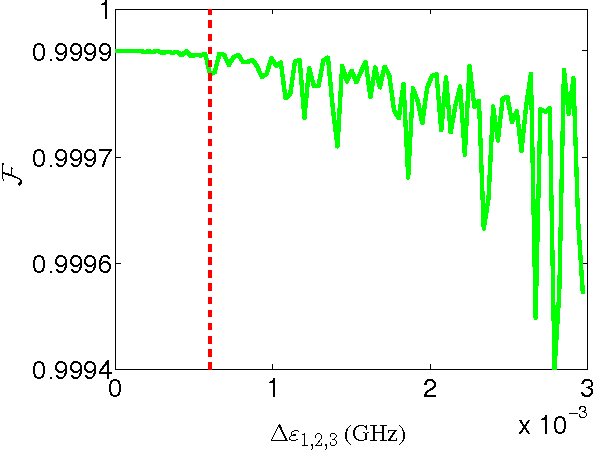
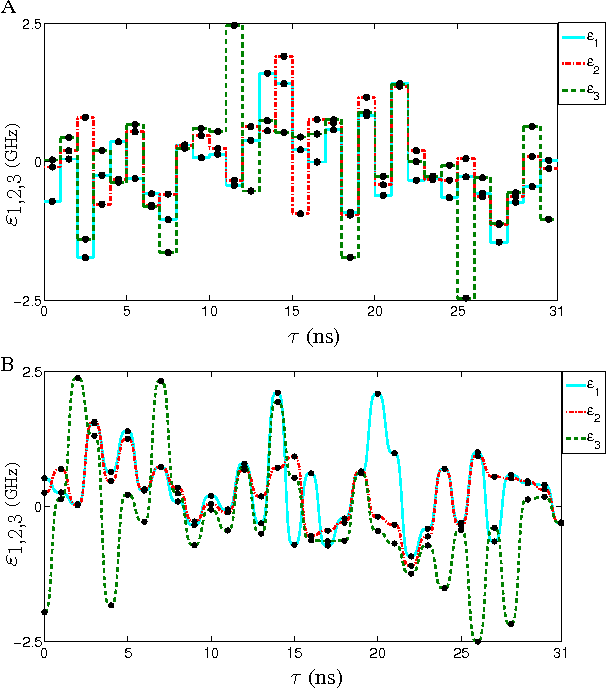
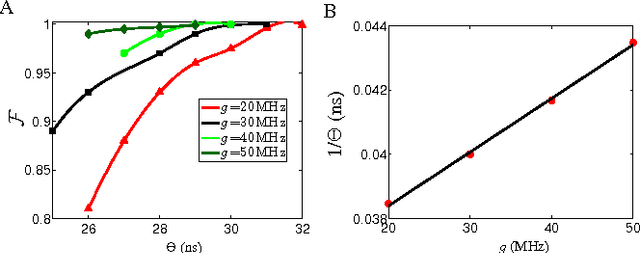
Three-qubit quantum gates are key ingredients for quantum error correction and quantum information processing. We generate quantum-control procedures to design three types of three-qubit gates, namely Toffoli, Controlled-Not-Not and Fredkin gates. The design procedures are applicable to a system comprising three nearest-neighbor-coupled superconducting artificial atoms. For each three-qubit gate, the numerical simulation of the proposed scheme achieves 99.9% fidelity, which is an accepted threshold fidelity for fault-tolerant quantum computing. We test our procedure in the presence of decoherence-induced noise as well as show its robustness against random external noise generated by the control electronics. The three-qubit gates are designed via the machine learning algorithm called Subspace-Selective Self-Adaptive Differential Evolution (SuSSADE).