Near-optimal sample complexity for convex tensor completion

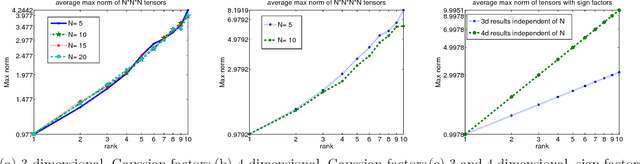
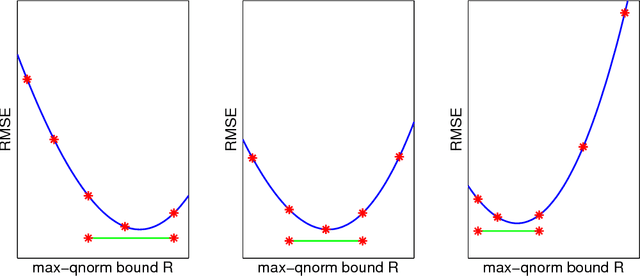
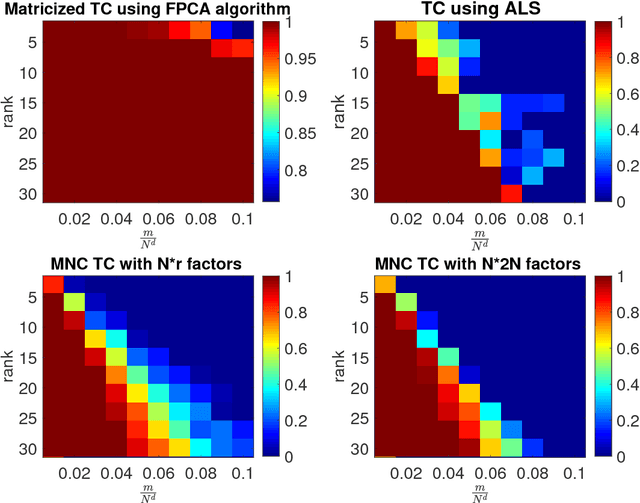
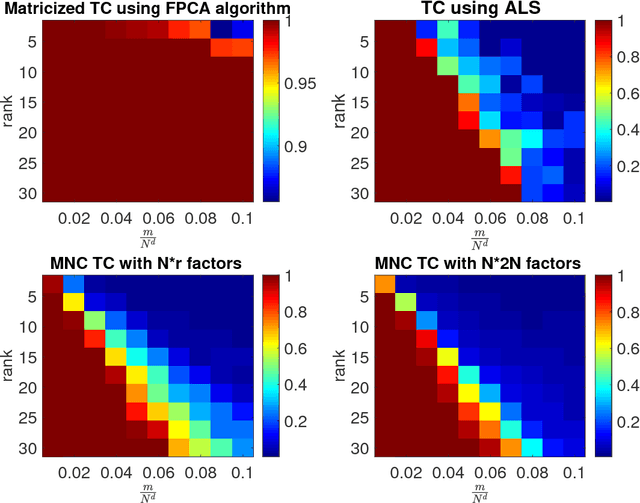
We analyze low rank tensor completion (TC) using noisy measurements of a subset of the tensor. Assuming a rank-$r$, order-$d$, $N \times N \times \cdots \times N$ tensor where $r=O(1)$, the best sampling complexity that was achieved is $O(N^{\frac{d}{2}})$, which is obtained by solving a tensor nuclear-norm minimization problem. However, this bound is significantly larger than the number of free variables in a low rank tensor which is $O(dN)$. In this paper, we show that by using an atomic-norm whose atoms are rank-$1$ sign tensors, one can obtain a sample complexity of $O(dN)$. Moreover, we generalize the matrix max-norm definition to tensors, which results in a max-quasi-norm (max-qnorm) whose unit ball has small Rademacher complexity. We prove that solving a constrained least squares estimation using either the convex atomic-norm or the nonconvex max-qnorm results in optimal sample complexity for the problem of low-rank tensor completion. Furthermore, we show that these bounds are nearly minimax rate-optimal. We also provide promising numerical results for max-qnorm constrained tensor completion, showing improved recovery results compared to matricization and alternating least squares.

Free energy-based reinforcement learning using a quantum processor

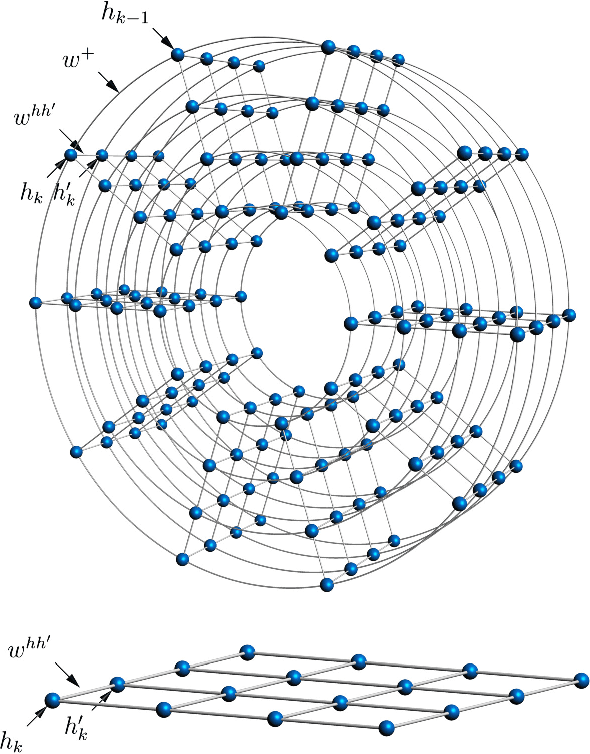
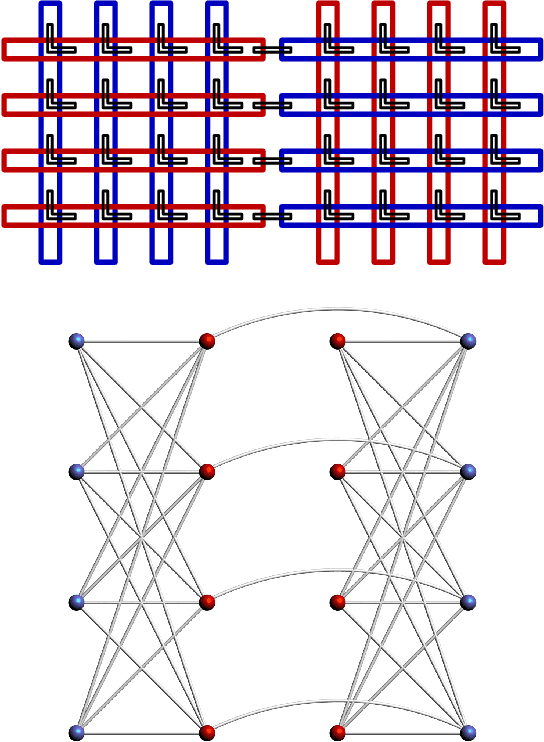
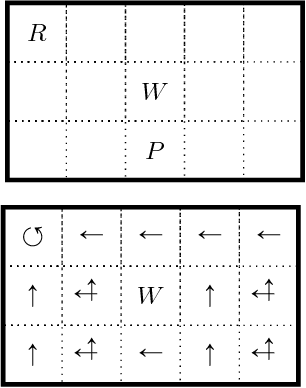
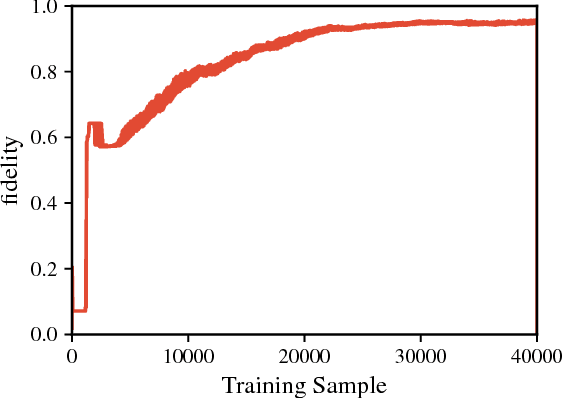
Recent theoretical and experimental results suggest the possibility of using current and near-future quantum hardware in challenging sampling tasks. In this paper, we introduce free energy-based reinforcement learning (FERL) as an application of quantum hardware. We propose a method for processing a quantum annealer's measured qubit spin configurations in approximating the free energy of a quantum Boltzmann machine (QBM). We then apply this method to perform reinforcement learning on the grid-world problem using the D-Wave 2000Q quantum annealer. The experimental results show that our technique is a promising method for harnessing the power of quantum sampling in reinforcement learning tasks.

Reinforcement Learning Using Quantum Boltzmann Machines

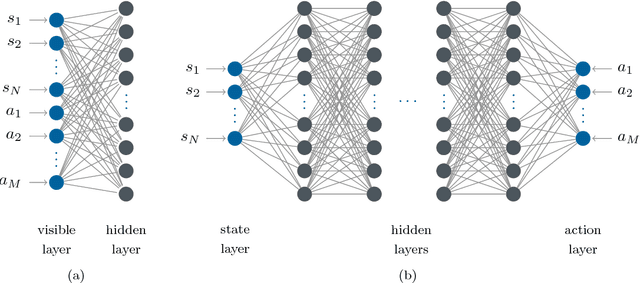
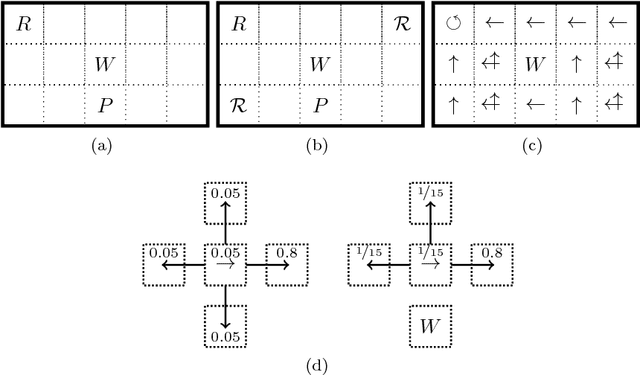
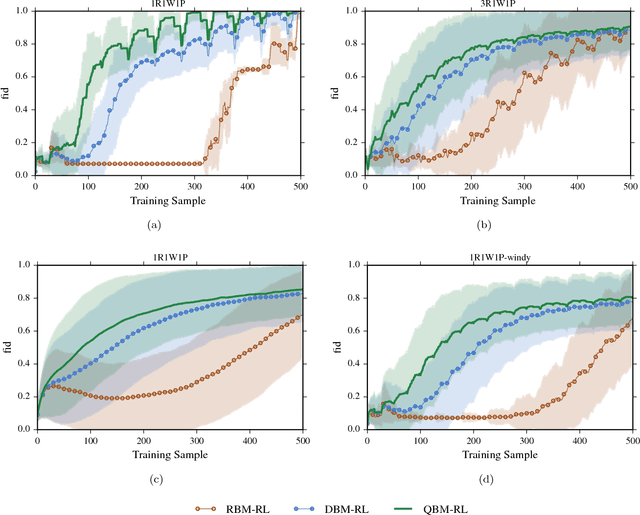
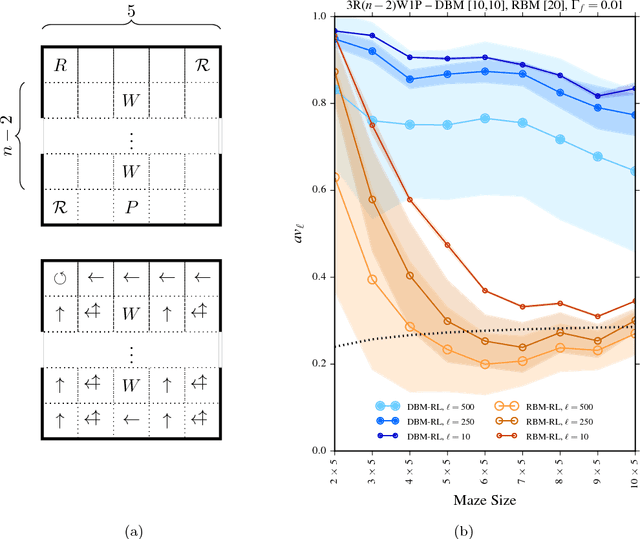
We investigate whether quantum annealers with select chip layouts can outperform classical computers in reinforcement learning tasks. We associate a transverse field Ising spin Hamiltonian with a layout of qubits similar to that of a deep Boltzmann machine (DBM) and use simulated quantum annealing (SQA) to numerically simulate quantum sampling from this system. We design a reinforcement learning algorithm in which the set of visible nodes representing the states and actions of an optimal policy are the first and last layers of the deep network. In absence of a transverse field, our simulations show that DBMs train more effectively than restricted Boltzmann machines (RBM) with the same number of weights. Since sampling from Boltzmann distributions of a DBM is not classically feasible, this is evidence of advantage of a non-Turing sampling oracle. We then develop a framework for training the network as a quantum Boltzmann machine (QBM) in the presence of a significant transverse field for reinforcement learning. This further improves the reinforcement learning method using DBMs.