Learning from few examples: Classifying sex from retinal images via deep learning

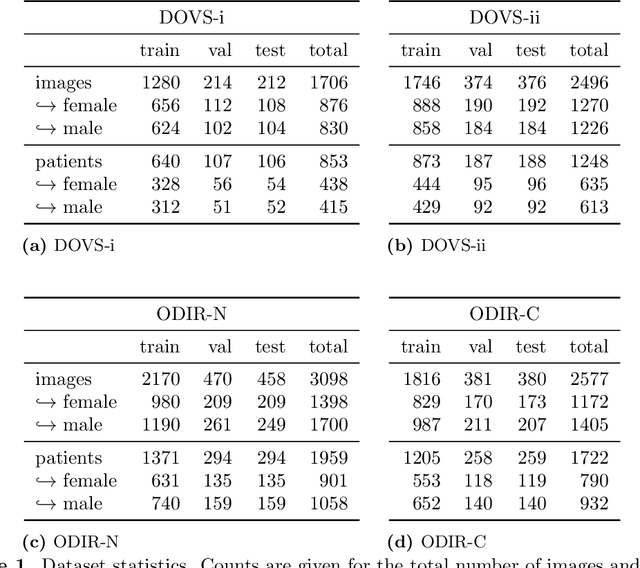
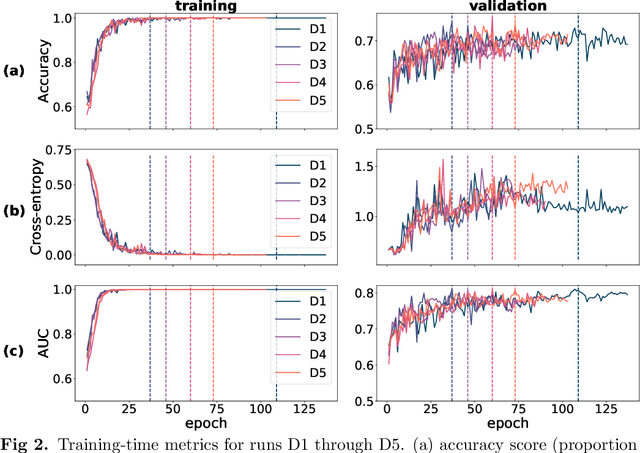
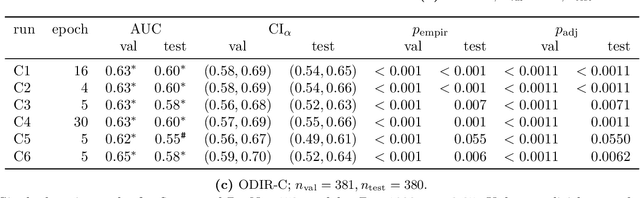
Deep learning has seen tremendous interest in medical imaging, particularly in the use of convolutional neural networks (CNNs) for developing automated diagnostic tools. The facility of its non-invasive acquisition makes retinal fundus imaging amenable to such automated approaches. Recent work in analyzing fundus images using CNNs relies on access to massive data for training and validation - hundreds of thousands of images. However, data residency and data privacy restrictions stymie the applicability of this approach in medical settings where patient confidentiality is a mandate. Here, we showcase results for the performance of DL on small datasets to classify patient sex from fundus images - a trait thought not to be present or quantifiable in fundus images until recently. We fine-tune a Resnet-152 model whose last layer has been modified for binary classification. In several experiments, we assess performance in the small dataset context using one private (DOVS) and one public (ODIR) data source. Our models, developed using approximately 2500 fundus images, achieved test AUC scores of up to 0.72 (95% CI: [0.67, 0.77]). This corresponds to a mere 25% decrease in performance despite a nearly 1000-fold decrease in the dataset size compared to prior work in the literature. Even with a hard task like sex categorization from retinal images, we find that classification is possible with very small datasets. Additionally, we perform domain adaptation experiments between DOVS and ODIR; explore the effect of data curation on training and generalizability; and investigate model ensembling to maximize CNN classifier performance in the context of small development datasets.

Sub-Gaussian Matrices on Sets: Optimal Tail Dependence and Applications

Random linear mappings are widely used in modern signal processing, compressed sensing and machine learning. These mappings may be used to embed the data into a significantly lower dimension while at the same time preserving useful information. This is done by approximately preserving the distances between data points, which are assumed to belong to $\mathbb{R}^n$. Thus, the performance of these mappings is usually captured by how close they are to an isometry on the data. Random Gaussian linear mappings have been the object of much study, while the sub-Gaussian settings is not yet fully understood. In the latter case, the performance depends on the sub-Gaussian norm of the rows. In many applications, e.g., compressed sensing, this norm may be large, or even growing with dimension, and thus it is important to characterize this dependence. We study when a sub-Gaussian matrix can become a near isometry on a set, show that previous best known dependence on the sub-Gaussian norm was sub-optimal, and present the optimal dependence. Our result not only answers a remaining question posed by Liaw, Mehrabian, Plan and Vershynin in 2017, but also generalizes their work. We also develop a new Bernstein type inequality for sub-exponential random variables, and a new Hanson-Wright inequality for quadratic forms of sub-Gaussian random variables, in both cases improving the bounds in the sub-Gaussian regime under moment constraints. Finally, we illustrate popular applications such as Johnson-Lindenstrauss embeddings, randomized sketches and blind demodulation, whose theoretical guarantees can be improved by our results in the sub-Gaussian case.

Near-optimal sample complexity for convex tensor completion

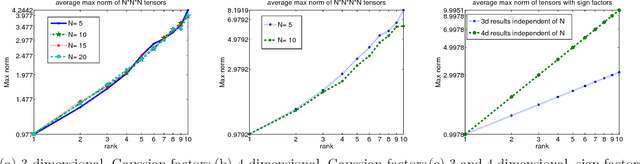
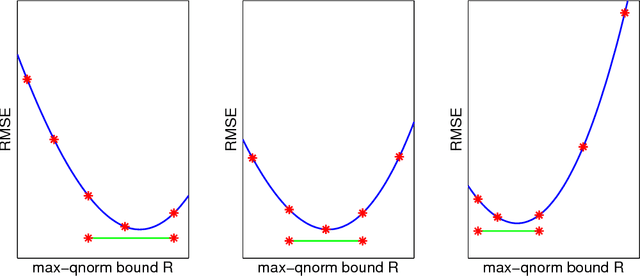
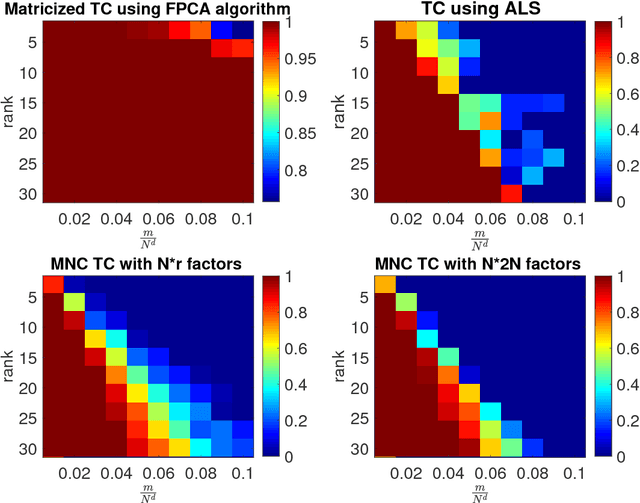
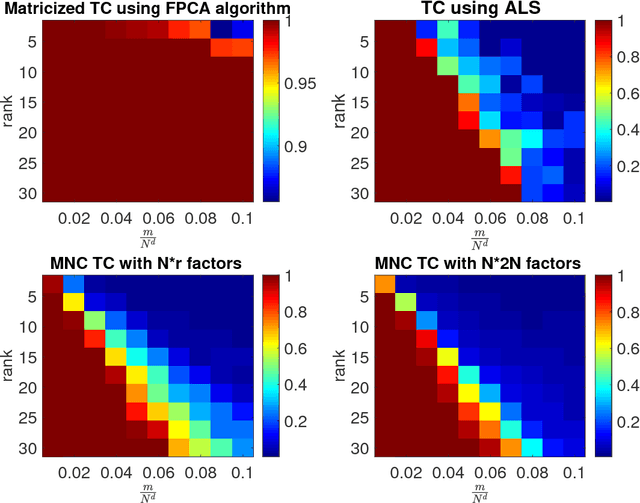
We analyze low rank tensor completion (TC) using noisy measurements of a subset of the tensor. Assuming a rank-$r$, order-$d$, $N \times N \times \cdots \times N$ tensor where $r=O(1)$, the best sampling complexity that was achieved is $O(N^{\frac{d}{2}})$, which is obtained by solving a tensor nuclear-norm minimization problem. However, this bound is significantly larger than the number of free variables in a low rank tensor which is $O(dN)$. In this paper, we show that by using an atomic-norm whose atoms are rank-$1$ sign tensors, one can obtain a sample complexity of $O(dN)$. Moreover, we generalize the matrix max-norm definition to tensors, which results in a max-quasi-norm (max-qnorm) whose unit ball has small Rademacher complexity. We prove that solving a constrained least squares estimation using either the convex atomic-norm or the nonconvex max-qnorm results in optimal sample complexity for the problem of low-rank tensor completion. Furthermore, we show that these bounds are nearly minimax rate-optimal. We also provide promising numerical results for max-qnorm constrained tensor completion, showing improved recovery results compared to matricization and alternating least squares.