A Cryogenic Memristive Neural Decoder for Fault-tolerant Quantum Error Correction

Neural decoders for quantum error correction (QEC) rely on neural networks to classify syndromes extracted from error correction codes and find appropriate recovery operators to protect logical information against errors. Despite the good performance of neural decoders, important practical requirements remain to be achieved, such as minimizing the decoding time to meet typical rates of syndrome generation in repeated error correction schemes, and ensuring the scalability of the decoding approach as the code distance increases. Designing a dedicated integrated circuit to perform the decoding task in co-integration with a quantum processor appears necessary to reach these decoding time and scalability requirements, as routing signals in and out of a cryogenic environment to be processed externally leads to unnecessary delays and an eventual wiring bottleneck. In this work, we report the design and performance analysis of a neural decoder inference accelerator based on an in-memory computing (IMC) architecture, where crossbar arrays of resistive memory devices are employed to both store the synaptic weights of the decoder neural network and perform analog matrix-vector multiplications during inference. In proof-of-concept numerical experiments supported by experimental measurements, we investigate the impact of TiO$_\textrm{x}$-based memristive devices' non-idealities on decoding accuracy. Hardware-aware training methods are developed to mitigate the loss in accuracy, allowing the memristive neural decoders to achieve a pseudo-threshold of $9.23\times 10^{-4}$ for the distance-three surface code, whereas the equivalent digital neural decoder achieves a pseudo-threshold of $1.01\times 10^{-3}$. This work provides a pathway to scalable, fast, and low-power cryogenic IMC hardware for integrated QEC.

Neural Error Mitigation of Near-Term Quantum Simulations

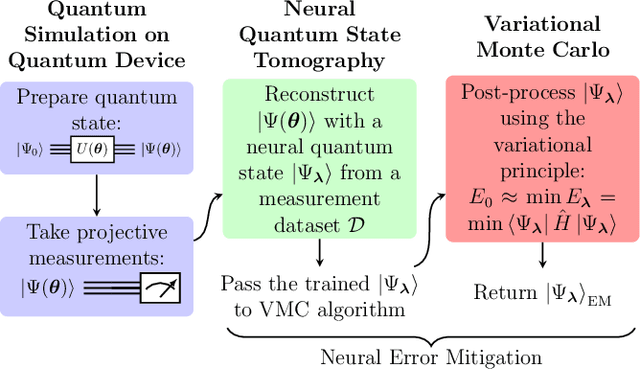
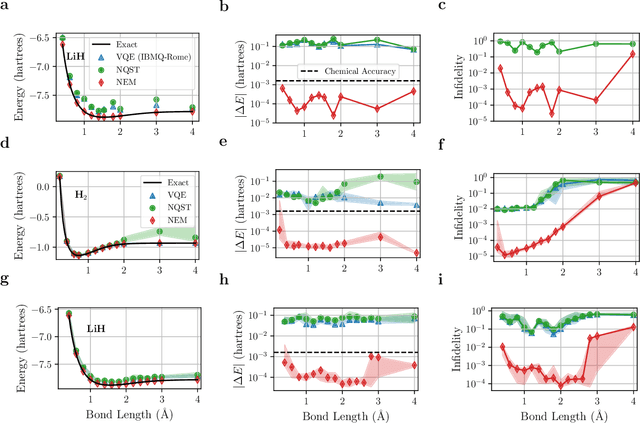
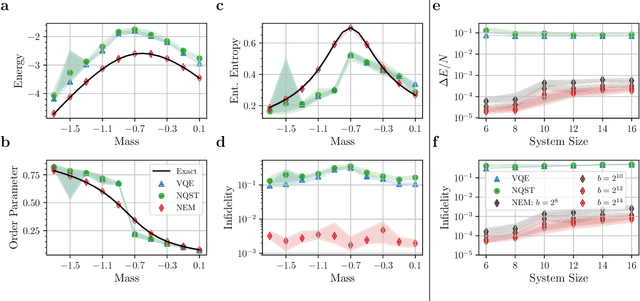
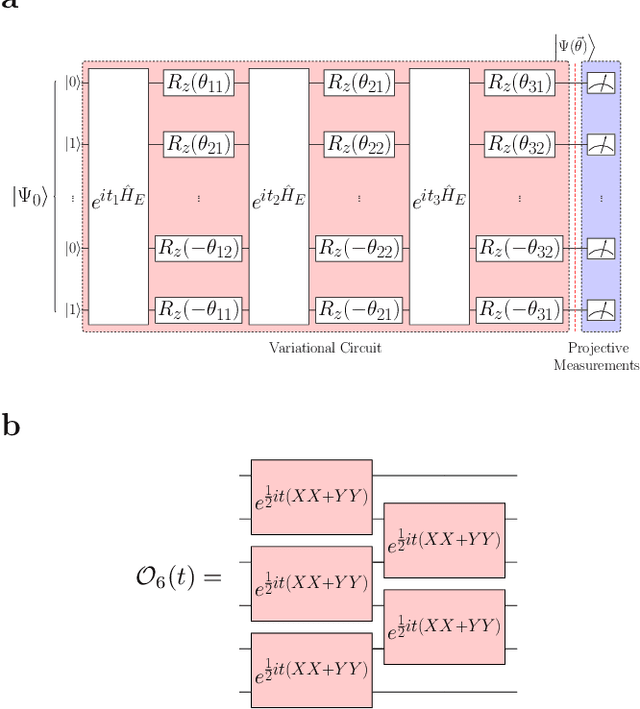
One of the promising applications of early quantum computers is the simulation of quantum systems. Variational methods for near-term quantum computers, such as the variational quantum eigensolver (VQE), are a promising approach to finding ground states of quantum systems relevant in physics, chemistry, and materials science. These approaches, however, are constrained by the effects of noise as well as the limited quantum resources of near-term quantum hardware, motivating the need for quantum error mitigation techniques to reduce the effects of noise. Here we introduce $\textit{neural error mitigation}$, a novel method that uses neural networks to improve estimates of ground states and ground-state observables obtained using VQE on near-term quantum computers. To demonstrate our method's versatility, we apply neural error mitigation to finding the ground states of H$_2$ and LiH molecular Hamiltonians, as well as the lattice Schwinger model. Our results show that neural error mitigation improves the numerical and experimental VQE computation to yield low-energy errors, low infidelities, and accurate estimations of more-complex observables like order parameters and entanglement entropy, without requiring additional quantum resources. Additionally, neural error mitigation is agnostic to both the quantum hardware and the particular noise channel, making it a versatile tool for quantum simulation. Applying quantum many-body machine learning techniques to error mitigation, our method is a promising strategy for extending the reach of near-term quantum computers to solve complex quantum simulation problems.