Continuous Prediction with Experts' Advice

Prediction with experts' advice is one of the most fundamental problems in online learning and captures many of its technical challenges. A recent line of work has looked at online learning through the lens of differential equations and continuous-time analysis. This viewpoint has yielded optimal results for several problems in online learning. In this paper, we employ continuous-time stochastic calculus in order to study the discrete-time experts' problem. We use these tools to design a continuous-time, parameter-free algorithm with improved guarantees for the quantile regret. We then develop an analogous discrete-time algorithm with a very similar analysis and identical quantile regret bounds. Finally, we design an anytime continuous-time algorithm with regret matching the optimal fixed-time rate when the gains are independent Brownian Motions; in many settings, this is the most difficult case. This gives some evidence that, even with adversarial gains, the optimal anytime and fixed-time regrets may coincide.

Efficient and Optimal Fixed-Time Regret with Two Experts

Prediction with expert advice is a foundational problem in online learning. In instances with $T$ rounds and $n$ experts, the classical Multiplicative Weights Update method suffers at most $\sqrt{(T/2)\ln n}$ regret when $T$ is known beforehand. Moreover, this is asymptotically optimal when both $T$ and $n$ grow to infinity. However, when the number of experts $n$ is small/fixed, algorithms with better regret guarantees exist. Cover showed in 1967 a dynamic programming algorithm for the two-experts problem restricted to $\{0,1\}$ costs that suffers at most $\sqrt{T/2\pi} + O(1)$ regret with $O(T^2)$ pre-processing time. In this work, we propose an optimal algorithm for prediction with two experts' advice that works even for costs in $[0,1]$ and with $O(1)$ processing time per turn. Our algorithm builds up on recent work on the experts problem based on techniques and tools from stochastic calculus.

Regret Bounds without Lipschitz Continuity: Online Learning with Relative-Lipschitz Losses

In online convex optimization (OCO), Lipschitz continuity of the functions is commonly assumed in order to obtain sublinear regret. Moreover, many algorithms have only logarithmic regret when these functions are also strongly convex. Recently, researchers from convex optimization proposed the notions of "relative Lipschitz continuity" and "relative strong convexity". Both of the notions are generalizations of their classical counterparts. It has been shown that subgradient methods in the relative setting have performance analogous to their performance in the classical setting. In this work, we consider OCO for relative Lipschitz and relative strongly convex functions. We extend the known regret bounds for classical OCO algorithms to the relative setting. Specifically, we show regret bounds for the follow the regularized leader algorithms and a variant of online mirror descent. Due to the generality of these methods, these results yield regret bounds for a wide variety of OCO algorithms. Furthermore, we further extend the results to algorithms with extra regularization such as regularized dual averaging.

Online mirror descent and dual averaging: keeping pace in the dynamic case

Online mirror descent (OMD) and dual averaging (DA) are two fundamental algorithms for online convex optimization. They are known to have very similar (or even identical) performance guarantees in most scenarios when a \emph{fixed} learning rate is used. However, for \emph{dynamic} learning rates OMD is provably inferior to DA. It is known that, with a dynamic learning rate, OMD can suffer linear regret, even in common settings such as prediction with expert advice. This hints that the relationship between OMD and DA is not fully understood at present. In this paper, we modify the OMD algorithm by a simple technique that we call stabilization. We give essentially the same abstract regret bound for stabilized OMD and DA by modifying the classical OMD convergence analysis in a careful and modular way, yielding proofs that we believe to be clean and flexible. Simple corollaries of these bounds show that OMD with stabilization and DA enjoy the same performance guarantees in many applications even under dynamic learning rates. We also shed some light on the similarities between OMD and DA and show simple conditions under which stabilized OMD and DA generate the same iterates.

Optimal anytime regret with two experts

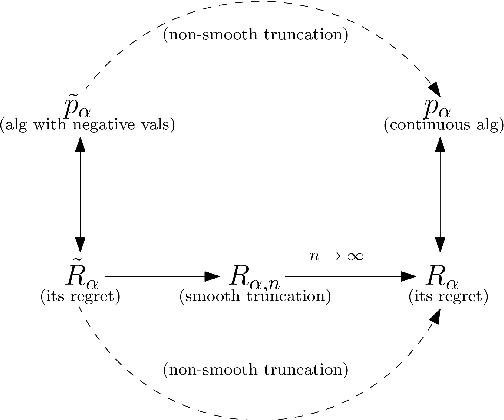
The multiplicative weights method is an algorithm for the problem of prediction with expert advice. It achieves the minimax regret asymptotically if the number of experts is large, and the time horizon is known in advance. Optimal algorithms are also known if there are exactly two or three experts, and the time horizon is known in advance. In the anytime setting, where the time horizon is not known in advance, algorithms can be obtained by the doubling trick, but they are not optimal, let alone practical. No minimax optimal algorithm was previously known in the anytime setting, regardless of the number of experts. We design the first minimax optimal algorithm for minimizing regret in the anytime setting. We consider the case of two experts, and prove that the optimal regret is $\gamma \sqrt{t} / 2$ at all time steps $t$, where $\gamma$ is a natural constant that arose 35 years ago in studying fundamental properties of Brownian motion. The algorithm is designed by considering a continuous analogue, which is solved using ideas from stochastic calculus.

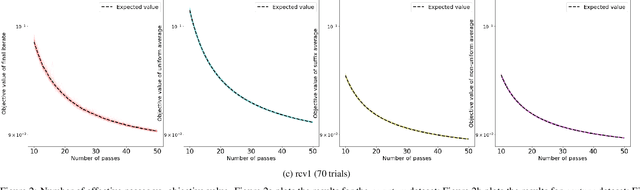
Simple and optimal high-probability bounds for strongly-convex stochastic gradient descent

We consider stochastic gradient descent algorithms for minimizing a non-smooth, strongly-convex function. Several forms of this algorithm, including suffix averaging, are known to achieve the optimal $O(1/T)$ convergence rate in expectation. We consider a simple, non-uniform averaging strategy of Lacoste-Julien et al. (2011) and prove that it achieves the optimal $O(1/T)$ convergence rate with high probability. Our proof uses a recently developed generalization of Freedman's inequality. Finally, we compare several of these algorithms experimentally and show that this non-uniform averaging strategy outperforms many standard techniques, and with smaller variance.

Tight Analyses for Non-Smooth Stochastic Gradient Descent

Consider the problem of minimizing functions that are Lipschitz and strongly convex, but not necessarily differentiable. We prove that after $T$ steps of stochastic gradient descent, the error of the final iterate is $O(\log(T)/T)$ with high probability. We also construct a function from this class for which the error of the final iterate of deterministic gradient descent is $\Omega(\log(T)/T)$. This shows that the upper bound is tight and that, in this setting, the last iterate of stochastic gradient descent has the same general error rate (with high probability) as deterministic gradient descent. This resolves both open questions posed by Shamir (2012). An intermediate step of our analysis proves that the suffix averaging method achieves error $O(1/T)$ with high probability, which is optimal (for any first-order optimization method). This improves results of Rakhlin (2012) and Hazan and Kale (2014), both of which achieved error $O(1/T)$, but only in expectation, and achieved a high probability error bound of $O(\log \log(T)/T)$, which is suboptimal. We prove analogous results for functions that are Lipschitz and convex, but not necessarily strongly convex or differentiable. After $T$ steps of stochastic gradient descent, the error of the final iterate is $O(\log(T)/\sqrt{T})$ with high probability, and there exists a function for which the error of the final iterate of deterministic gradient descent is $\Omega(\log(T)/\sqrt{T})$.

Submodular Functions: Learnability, Structure, and Optimization

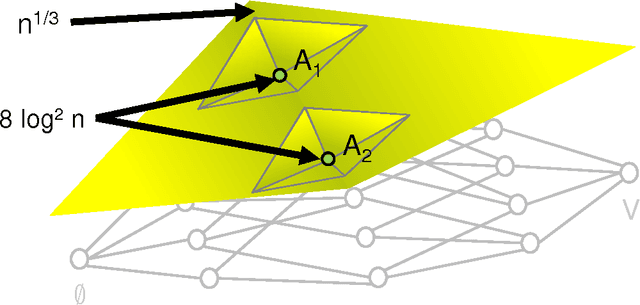
Submodular functions are discrete functions that model laws of diminishing returns and enjoy numerous algorithmic applications. They have been used in many areas, including combinatorial optimization, machine learning, and economics. In this work we study submodular functions from a learning theoretic angle. We provide algorithms for learning submodular functions, as well as lower bounds on their learnability. In doing so, we uncover several novel structural results revealing ways in which submodular functions can be both surprisingly structured and surprisingly unstructured. We provide several concrete implications of our work in other domains including algorithmic game theory and combinatorial optimization. At a technical level, this research combines ideas from many areas, including learning theory (distributional learning and PAC-style analyses), combinatorics and optimization (matroids and submodular functions), and pseudorandomness (lossless expander graphs).