A dual approach for federated learning
Paper and Code
Feb 04, 2022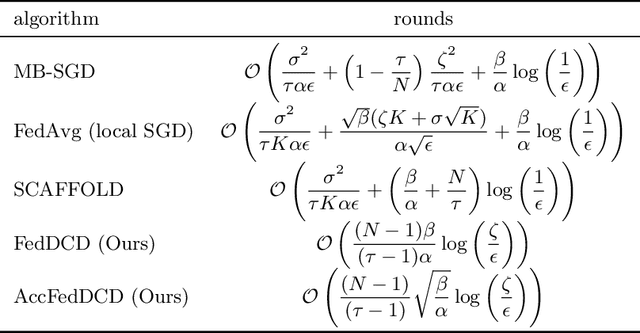
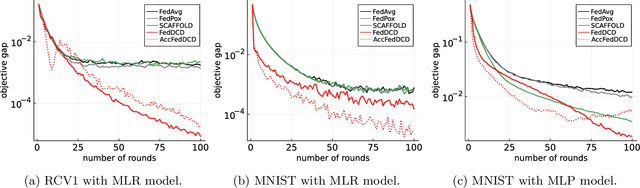
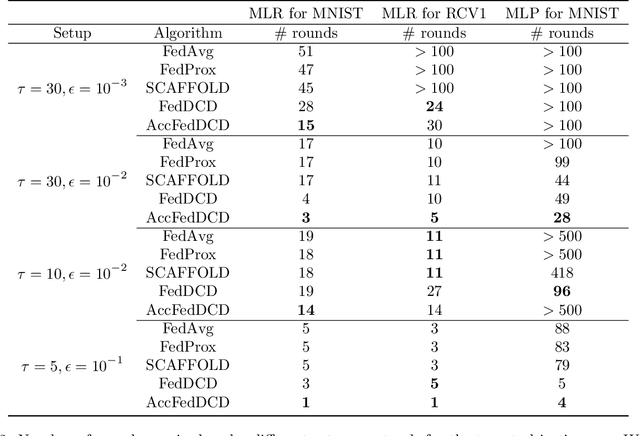
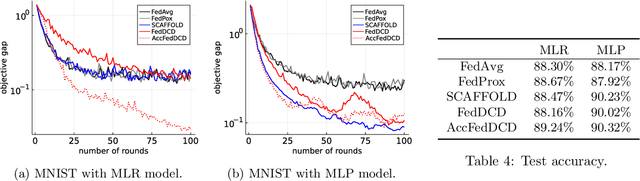
We study the federated optimization problem from a dual perspective and propose a new algorithm termed federated dual coordinate descent (FedDCD), which is based on a type of coordinate descent method developed by Necora et al.[Journal of Optimization Theory and Applications, 2017]. Additionally, we enhance the FedDCD method with inexact gradient oracles and Nesterov's acceleration. We demonstrate theoretically that our proposed approach achieves better convergence rates than the state-of-the-art primal federated optimization algorithms under certain situations. Numerical experiments on real-world datasets support our analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge