Asynchronous Distributed Optimization with Delay-free Parameters

Existing asynchronous distributed optimization algorithms often use diminishing step-sizes that cause slow practical convergence, or use fixed step-sizes that depend on and decrease with an upper bound of the delays. Not only are such delay bounds hard to obtain in advance, but they also tend to be large and rarely attained, resulting in unnecessarily slow convergence. This paper develops asynchronous versions of two distributed algorithms, Prox-DGD and DGD-ATC, for solving consensus optimization problems over undirected networks. In contrast to alternatives, our algorithms can converge to the fixed point set of their synchronous counterparts using step-sizes that are independent of the delays. We establish convergence guarantees for strongly and weakly convex problems under both partial and total asynchrony. We also show that the convergence speed of the two asynchronous methods adapts to the actual level of asynchrony rather than being constrained by the worst-case. Numerical experiments demonstrate a strong practical performance of our asynchronous algorithms.

Federated Learning for IoUT: Concepts, Applications, Challenges and Opportunities

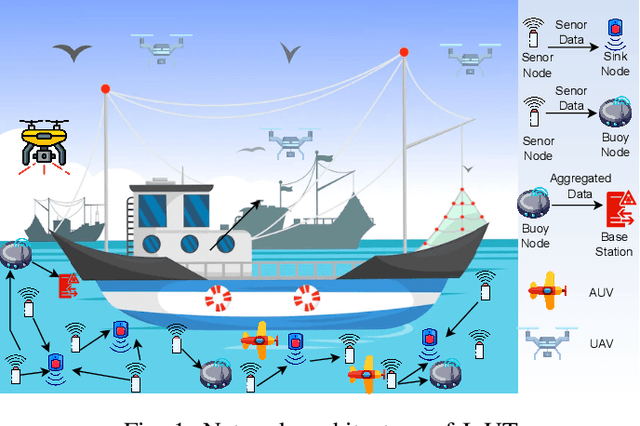
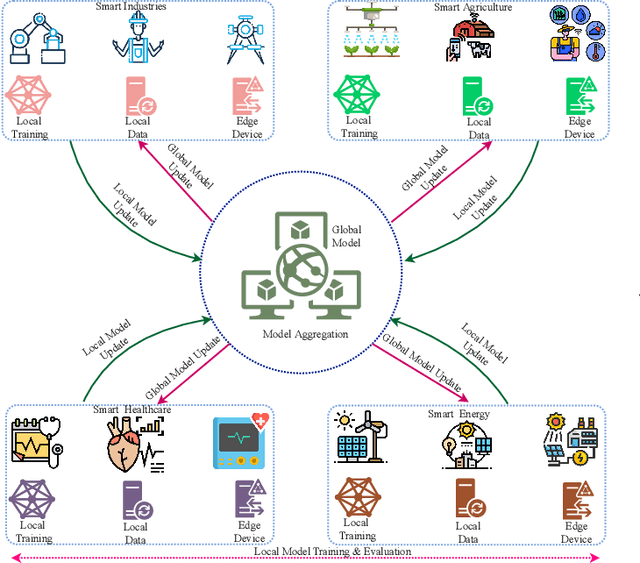
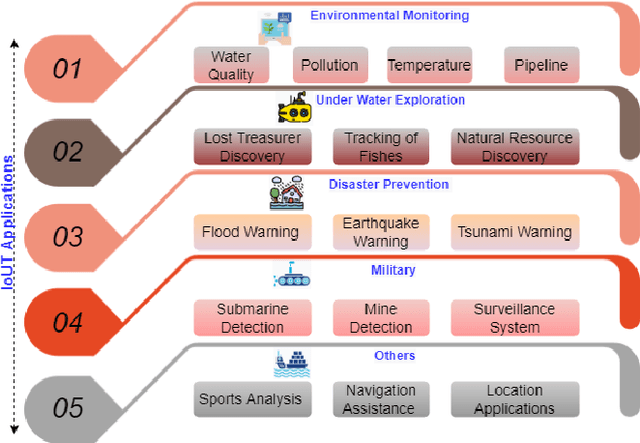
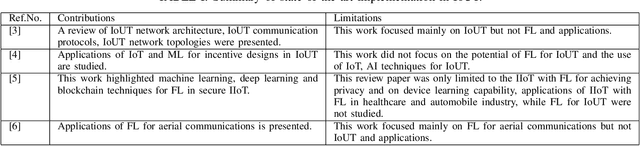
Internet of Underwater Things (IoUT) have gained rapid momentum over the past decade with applications spanning from environmental monitoring and exploration, defence applications, etc. The traditional IoUT systems use machine learning (ML) approaches which cater the needs of reliability, efficiency and timeliness. However, an extensive review of the various studies conducted highlight the significance of data privacy and security in IoUT frameworks as a predominant factor in achieving desired outcomes in mission critical applications. Federated learning (FL) is a secured, decentralized framework which is a recent development in machine learning, that will help in fulfilling the challenges faced by conventional ML approaches in IoUT. This paper presents an overview of the various applications of FL in IoUT, its challenges, open issues and indicates direction of future research prospects.

Delay-adaptive step-sizes for asynchronous learning

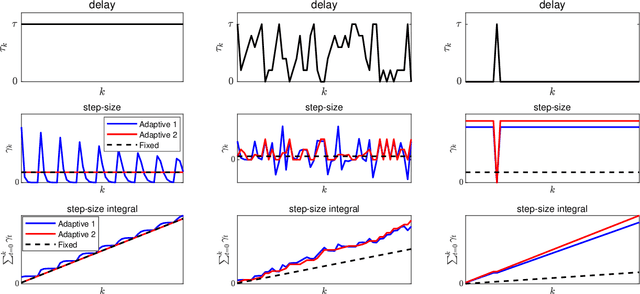
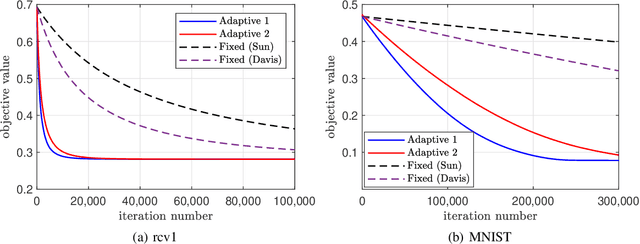
In scalable machine learning systems, model training is often parallelized over multiple nodes that run without tight synchronization. Most analysis results for the related asynchronous algorithms use an upper bound on the information delays in the system to determine learning rates. Not only are such bounds hard to obtain in advance, but they also result in unnecessarily slow convergence. In this paper, we show that it is possible to use learning rates that depend on the actual time-varying delays in the system. We develop general convergence results for delay-adaptive asynchronous iterations and specialize these to proximal incremental gradient descent and block-coordinate descent algorithms. For each of these methods, we demonstrate how delays can be measured on-line, present delay-adaptive step-size policies, and illustrate their theoretical and practical advantages over the state-of-the-art.

Communication-efficient Variance-reduced Stochastic Gradient Descent

We consider the problem of communication efficient distributed optimization where multiple nodes exchange important algorithm information in every iteration to solve large problems. In particular, we focus on the stochastic variance-reduced gradient and propose a novel approach to make it communication-efficient. That is, we compress the communicated information to a few bits while preserving the linear convergence rate of the original uncompressed algorithm. Comprehensive theoretical and numerical analyses on real datasets reveal that our algorithm can significantly reduce the communication complexity, by as much as 95\%, with almost no noticeable penalty. Moreover, it is much more robust to quantization (in terms of maintaining the true minimizer and the convergence rate) than the state-of-the-art algorithms for solving distributed optimization problems. Our results have important implications for using machine learning over internet-of-things and mobile networks.