Delay-adaptive step-sizes for asynchronous learning

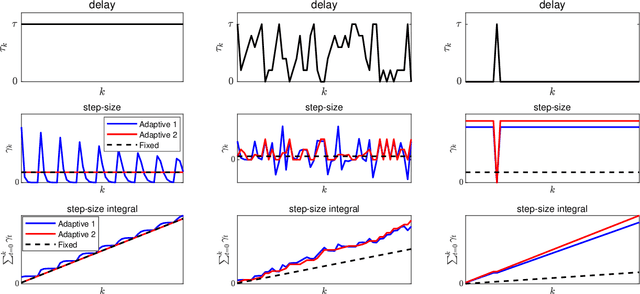
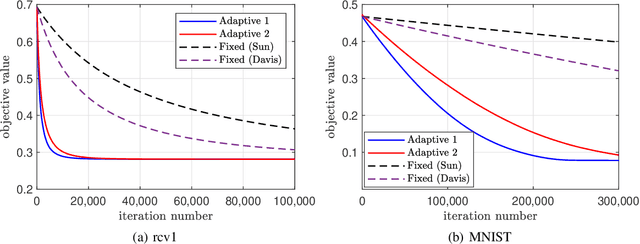
In scalable machine learning systems, model training is often parallelized over multiple nodes that run without tight synchronization. Most analysis results for the related asynchronous algorithms use an upper bound on the information delays in the system to determine learning rates. Not only are such bounds hard to obtain in advance, but they also result in unnecessarily slow convergence. In this paper, we show that it is possible to use learning rates that depend on the actual time-varying delays in the system. We develop general convergence results for delay-adaptive asynchronous iterations and specialize these to proximal incremental gradient descent and block-coordinate descent algorithms. For each of these methods, we demonstrate how delays can be measured on-line, present delay-adaptive step-size policies, and illustrate their theoretical and practical advantages over the state-of-the-art.

Asynchronous Iterations in Optimization: New Sequence Results and Sharper Algorithmic Guarantees

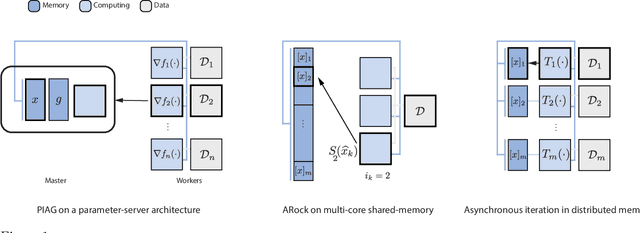
We introduce novel convergence results for asynchronous iterations which appear in the analysis of parallel and distributed optimization algorithms. The results are simple to apply and give explicit estimates for how the degree of asynchrony impacts the convergence rates of the iterates. Our results shorten, streamline and strengthen existing convergence proofs for several asynchronous optimization methods, and allow us to establish convergence guarantees for popular algorithms that were thus far lacking a complete theoretical understanding. Specifically, we use our results to derive better iteration complexity bounds for proximal incremental aggregated gradient methods, to provide less conservative analyses of the speedup conditions for asynchronous block-coordinate implementations of Krasnoselskii-Mann iterations, and to quantify the convergence rates for totally asynchronous iterations under various assumptions on communication delays and update rates.

Distributed learning with compressed gradients

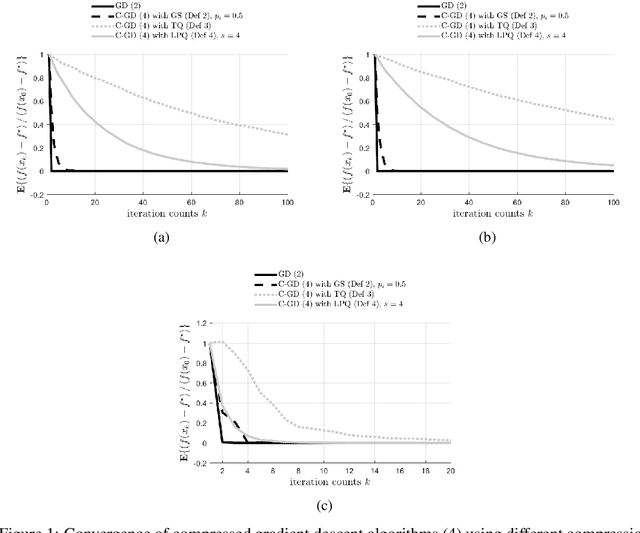
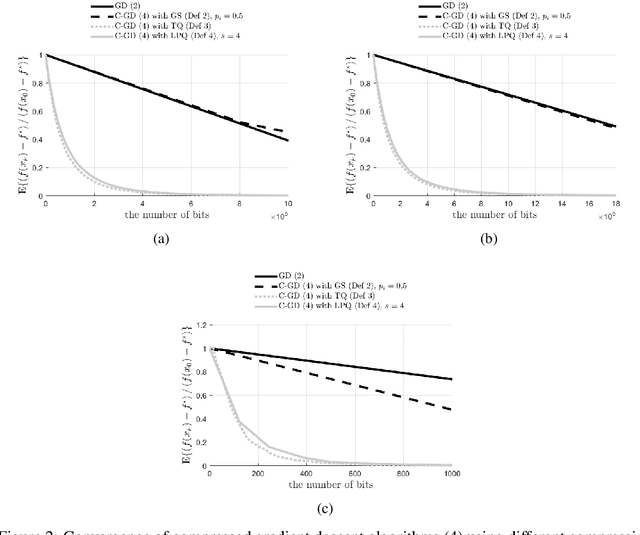
Asynchronous computation and gradient compression have emerged as two key techniques for achieving scalability in distributed optimization for large-scale machine learning. This paper presents a unified analysis framework for distributed gradient methods operating with staled and compressed gradients. Non-asymptotic bounds on convergence rates and information exchange are derived for several optimization algorithms. These bounds give explicit expressions for step-sizes and characterize how the amount of asynchrony and the compression accuracy affect iteration and communication complexity guarantees. Numerical results highlight convergence properties of different gradient compression algorithms and confirm that fast convergence under limited information exchange is indeed possible.

Analysis and Implementation of an Asynchronous Optimization Algorithm for the Parameter Server

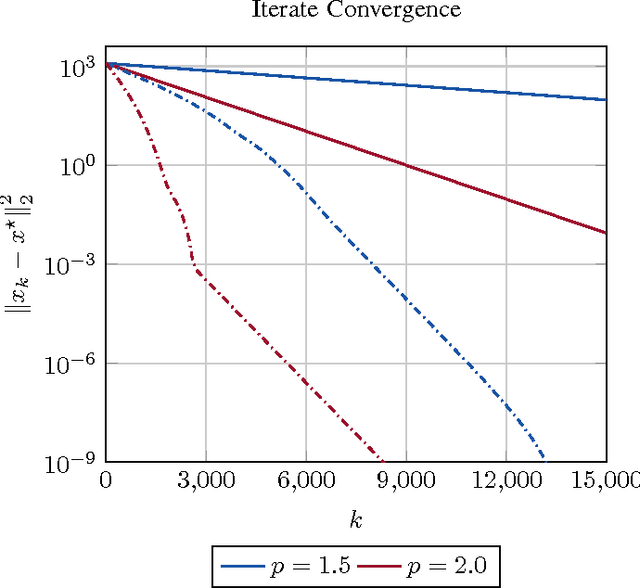
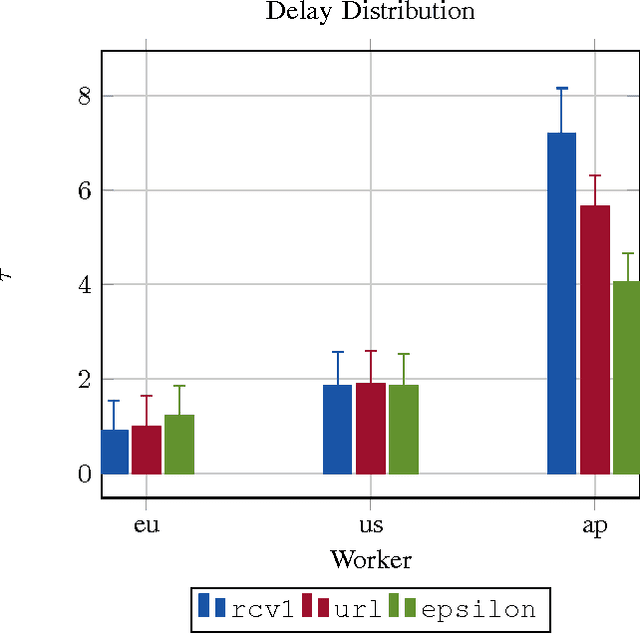
This paper presents an asynchronous incremental aggregated gradient algorithm and its implementation in a parameter server framework for solving regularized optimization problems. The algorithm can handle both general convex (possibly non-smooth) regularizers and general convex constraints. When the empirical data loss is strongly convex, we establish linear convergence rate, give explicit expressions for step-size choices that guarantee convergence to the optimum, and bound the associated convergence factors. The expressions have an explicit dependence on the degree of asynchrony and recover classical results under synchronous operation. Simulations and implementations on commercial compute clouds validate our findings.

An Asynchronous Mini-Batch Algorithm for Regularized Stochastic Optimization

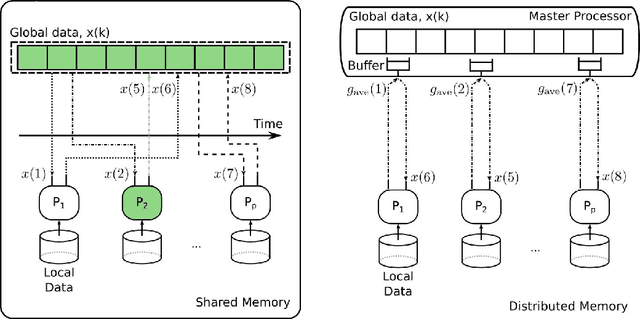
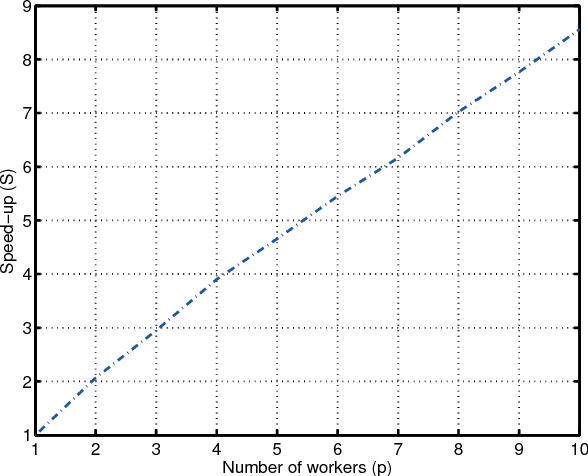
Mini-batch optimization has proven to be a powerful paradigm for large-scale learning. However, the state of the art parallel mini-batch algorithms assume synchronous operation or cyclic update orders. When worker nodes are heterogeneous (due to different computational capabilities or different communication delays), synchronous and cyclic operations are inefficient since they will leave workers idle waiting for the slower nodes to complete their computations. In this paper, we propose an asynchronous mini-batch algorithm for regularized stochastic optimization problems with smooth loss functions that eliminates idle waiting and allows workers to run at their maximal update rates. We show that by suitably choosing the step-size values, the algorithm achieves a rate of the order $O(1/\sqrt{T})$ for general convex regularization functions, and the rate $O(1/T)$ for strongly convex regularization functions, where $T$ is the number of iterations. In both cases, the impact of asynchrony on the convergence rate of our algorithm is asymptotically negligible, and a near-linear speedup in the number of workers can be expected. Theoretical results are confirmed in real implementations on a distributed computing infrastructure.