Asynchronous Iterations in Optimization: New Sequence Results and Sharper Algorithmic Guarantees
Paper and Code
Sep 09, 2021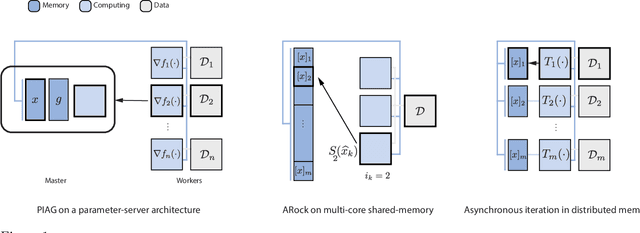
We introduce novel convergence results for asynchronous iterations which appear in the analysis of parallel and distributed optimization algorithms. The results are simple to apply and give explicit estimates for how the degree of asynchrony impacts the convergence rates of the iterates. Our results shorten, streamline and strengthen existing convergence proofs for several asynchronous optimization methods, and allow us to establish convergence guarantees for popular algorithms that were thus far lacking a complete theoretical understanding. Specifically, we use our results to derive better iteration complexity bounds for proximal incremental aggregated gradient methods, to provide less conservative analyses of the speedup conditions for asynchronous block-coordinate implementations of Krasnoselskii-Mann iterations, and to quantify the convergence rates for totally asynchronous iterations under various assumptions on communication delays and update rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge