Enforcing Biconnectivity in Multi-robot Systems

Connectivity maintenance is an essential task in multi-robot systems and it has received a considerable attention during the last years. A connected system can be broken into two or more subsets simply if a single robot fails. A more robust communication can be achieved if the network connectivity is guaranteed in the case of one-robot failures. The resulting network is called biconnected. In \cite{Zareh2016biconnectivitycheck}, we presented a criterion for biconnectivity check, which basically determines a lower bound on the third-smallest eigenvalue of the Laplacian matrix. In this paper, we introduce a decentralized gradient-based protocol to increase the value of the third-smallest eigenvalue of the Laplacian matrix, when the biconnectivity check fails. We also introduce a decentralized algorithm to estimate the eigenvectors of the Laplacian matrix, which are used for defining the gradient. Simulations show the effectiveness of the theoretical findings.

Decentralized Biconnectivity Conditions in Multi-robot Systems

The network connectivity in a group of cooperative robots can be easily broken if one of them loses its connectivity with the rest of the group. In case of having robustness with respect to one-robot-fail, the communication network is termed biconnected. In simple words, to have a biconnected network graph, we need to prove that there exists no articulation point. We propose a decentralized approach that provides sufficient conditions for biconnectivity of the network, and we prove that these conditions are related to the third smallest eigenvalue of the Laplacian matrix. Data exchange among the robots is supposed to be neighbor-to-neighbor.

Consensus on the average in arbitrary directed network topologies with time-delays

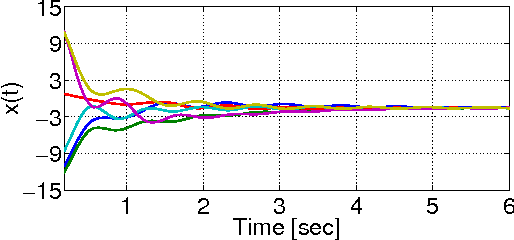
In this preliminary paper we study the stability property of a consensus on the average algorithm in arbitrary directed graphs with respect to communication/sensing time-delays. The proposed algorithm adds a storage variable to the agents' states so that the information about the average of the states is preserved despite the algorithm iterations are performed in an arbitrary strongly connected directed graph. We prove that for any network topology and choice of design parameters the consensus on the average algorithm is stable for sufficiently small delays. We provide simulations and numerical results to estimate the maximum delay allowed by an arbitrary unbalanced directed network topology.