Risk-Averse Certification of Bayesian Neural Networks

In light of the inherently complex and dynamic nature of real-world environments, incorporating risk measures is crucial for the robustness evaluation of deep learning models. In this work, we propose a Risk-Averse Certification framework for Bayesian neural networks called RAC-BNN. Our method leverages sampling and optimisation to compute a sound approximation of the output set of a BNN, represented using a set of template polytopes. To enhance robustness evaluation, we integrate a coherent distortion risk measure--Conditional Value at Risk (CVaR)--into the certification framework, providing probabilistic guarantees based on empirical distributions obtained through sampling. We validate RAC-BNN on a range of regression and classification benchmarks and compare its performance with a state-of-the-art method. The results show that RAC-BNN effectively quantifies robustness under worst-performing risky scenarios, and achieves tighter certified bounds and higher efficiency in complex tasks.

Uncertainty-Aware Decision-Making and Planning for Autonomous Forced Merging

In this paper, we develop an uncertainty-aware decision-making and motion-planning method for an autonomous ego vehicle in forced merging scenarios, considering the motion uncertainty of surrounding vehicles. The method dynamically captures the uncertainty of surrounding vehicles by online estimation of their acceleration bounds, enabling a reactive but rapid understanding of the uncertainty characteristics of the surrounding vehicles. By leveraging these estimated bounds, a non-conservative forward occupancy of surrounding vehicles is predicted over a horizon, which is incorporated in both the decision-making process and the motion-planning strategy, to enhance the resilience and safety of the planned reference trajectory. The method successfully fulfills the tasks in challenging forced merging scenarios, and the properties are illustrated by comparison with several alternative approaches.

Robust Predictive Motion Planning by Learning Obstacle Uncertainty

Safe motion planning for robotic systems in dynamic environments is nontrivial in the presence of uncertain obstacles, where estimation of obstacle uncertainties is crucial in predicting future motions of dynamic obstacles. The worst-case characterization gives a conservative uncertainty prediction and may result in infeasible motion planning for the ego robotic system. In this paper, an efficient, robust, and safe motion-planing algorithm is developed by learning the obstacle uncertainties online. More specifically, the unknown yet intended control set of obstacles is efficiently computed by solving a linear programming problem. The learned control set is used to compute forward reachable sets of obstacles that are less conservative than the worst-case prediction. Based on the forward prediction, a robust model predictive controller is designed to compute a safe reference trajectory for the ego robotic system that remains outside the reachable sets of obstacles over the prediction horizon. The method is applied to a car-like mobile robot in both simulations and hardware experiments to demonstrate its effectiveness.

Integrated Sensing and Communication with Massive MIMO: A Unified Tensor Approach for Channel and Target Parameter Estimation

Benefitting from the vast spatial degrees of freedom, the amalgamation of integrated sensing and communication (ISAC) and massive multiple-input multiple-output (MIMO) is expected to simultaneously improve spectral and energy efficiencies as well as the sensing capability. However, a large number of antennas deployed in massive MIMO-ISAC raises critical challenges in acquiring both accurate channel state information and target parameter information. To overcome these two challenges with a unified framework, we first analyze their underlying system models and then propose a novel tensor-based approach that addresses both the channel estimation and target sensing problems. Specifically, by parameterizing the high-dimensional communication channel exploiting a small number of physical parameters, we associate the channel state information with the sensing parameters of targets in terms of angular, delay, and Doppler dimensions. Then, we propose a shared training pattern adopting the same time-frequency resources such that both the channel estimation and target parameter estimation can be formulated as a canonical polyadic decomposition problem with a similar mathematical expression. On this basis, we first investigate the uniqueness condition of the tensor factorization and the maximum number of resolvable targets by utilizing the specific Vandermonde

Policy Evaluation in Distributional LQR

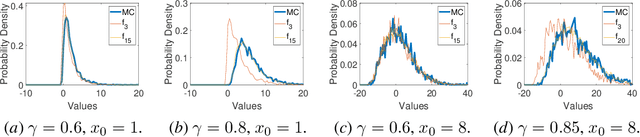
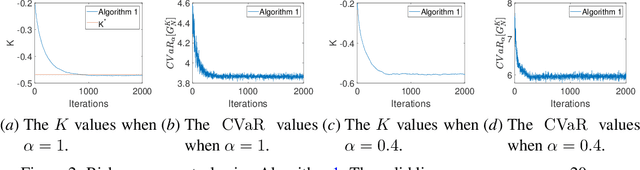
Distributional reinforcement learning (DRL) enhances the understanding of the effects of the randomness in the environment by letting agents learn the distribution of a random return, rather than its expected value as in standard RL. At the same time, a main challenge in DRL is that policy evaluation in DRL typically relies on the representation of the return distribution, which needs to be carefully designed. In this paper, we address this challenge for a special class of DRL problems that rely on linear quadratic regulator (LQR) for control, advocating for a new distributional approach to LQR, which we call \emph{distributional LQR}. Specifically, we provide a closed-form expression of the distribution of the random return which, remarkably, is applicable to all exogenous disturbances on the dynamics, as long as they are independent and identically distributed (i.i.d.). While the proposed exact return distribution consists of infinitely many random variables, we show that this distribution can be approximated by a finite number of random variables, and the associated approximation error can be analytically bounded under mild assumptions. Using the approximate return distribution, we propose a zeroth-order policy gradient algorithm for risk-averse LQR using the Conditional Value at Risk (CVaR) as a measure of risk. Numerical experiments are provided to illustrate our theoretical results.