Unveiling the Potential of Robustness in Evaluating Causal Inference Models

The growing demand for personalized decision-making has led to a surge of interest in estimating the Conditional Average Treatment Effect (CATE). The intersection of machine learning and causal inference has yielded various effective CATE estimators. However, deploying these estimators in practice is often hindered by the absence of counterfactual labels, making it challenging to select the desirable CATE estimator using conventional model selection procedures like cross-validation. Existing approaches for CATE estimator selection, such as plug-in and pseudo-outcome metrics, face two inherent challenges. Firstly, they are required to determine the metric form and the underlying machine learning models for fitting nuisance parameters or plug-in learners. Secondly, they lack a specific focus on selecting a robust estimator. To address these challenges, this paper introduces a novel approach, the Distributionally Robust Metric (DRM), for CATE estimator selection. The proposed DRM not only eliminates the need to fit additional models but also excels at selecting a robust CATE estimator. Experimental studies demonstrate the efficacy of the DRM method, showcasing its consistent effectiveness in identifying superior estimators while mitigating the risk of selecting inferior ones.

The Causal Impact of Credit Lines on Spending Distributions

Consumer credit services offered by e-commerce platforms provide customers with convenient loan access during shopping and have the potential to stimulate sales. To understand the causal impact of credit lines on spending, previous studies have employed causal estimators, based on direct regression (DR), inverse propensity weighting (IPW), and double machine learning (DML) to estimate the treatment effect. However, these estimators do not consider the notion that an individual's spending can be understood and represented as a distribution, which captures the range and pattern of amounts spent across different orders. By disregarding the outcome as a distribution, valuable insights embedded within the outcome distribution might be overlooked. This paper develops a distribution-valued estimator framework that extends existing real-valued DR-, IPW-, and DML-based estimators to distribution-valued estimators within Rubin's causal framework. We establish their consistency and apply them to a real dataset from a large e-commerce platform. Our findings reveal that credit lines positively influence spending across all quantiles; however, as credit lines increase, consumers allocate more to luxuries (higher quantiles) than necessities (lower quantiles).

Probabilistic Learning of Multivariate Time Series with Temporal Irregularity

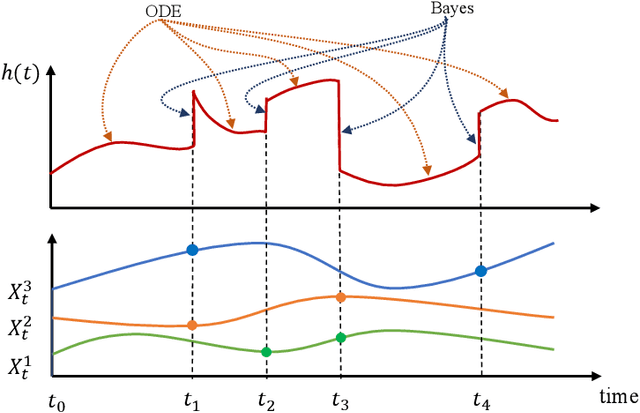
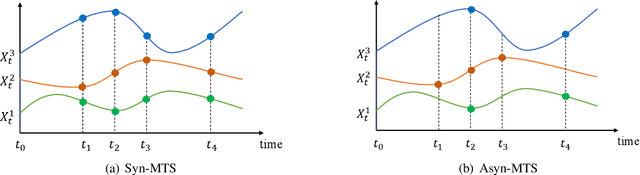
Multivariate sequential data collected in practice often exhibit temporal irregularities, including nonuniform time intervals and component misalignment. However, if uneven spacing and asynchrony are endogenous characteristics of the data rather than a result of insufficient observation, the information content of these irregularities plays a defining role in characterizing the multivariate dependence structure. Existing approaches for probabilistic forecasting either overlook the resulting statistical heterogeneities, are susceptible to imputation biases, or impose parametric assumptions on the data distribution. This paper proposes an end-to-end solution that overcomes these limitations by allowing the observation arrival times to play the central role of model construction, which is at the core of temporal irregularities. To acknowledge temporal irregularities, we first enable unique hidden states for components so that the arrival times can dictate when, how, and which hidden states to update. We then develop a conditional flow representation to non-parametrically represent the data distribution, which is typically non-Gaussian, and supervise this representation by carefully factorizing the log-likelihood objective to select conditional information that facilitates capturing time variation and path dependency. The broad applicability and superiority of the proposed solution are confirmed by comparing it with existing approaches through ablation studies and testing on real-world datasets.

Deep into The Domain Shift: Transfer Learning through Dependence Regularization

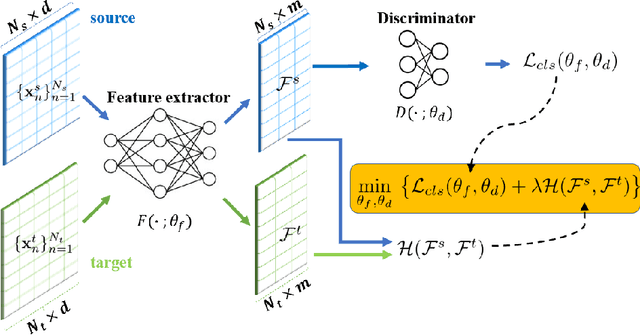
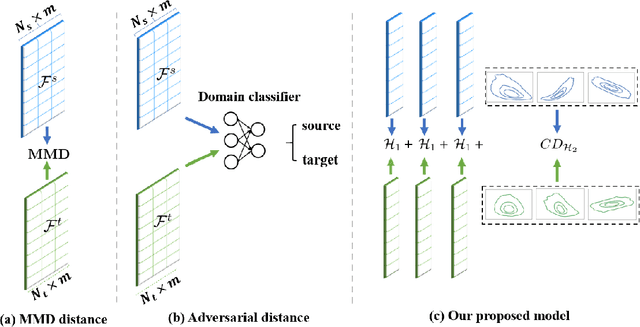
Classical Domain Adaptation methods acquire transferability by regularizing the overall distributional discrepancies between features in the source domain (labeled) and features in the target domain (unlabeled). They often do not differentiate whether the domain differences come from the marginals or the dependence structures. In many business and financial applications, the labeling function usually has different sensitivities to the changes in the marginals versus changes in the dependence structures. Measuring the overall distributional differences will not be discriminative enough in acquiring transferability. Without the needed structural resolution, the learned transfer is less optimal. This paper proposes a new domain adaptation approach in which one can measure the differences in the internal dependence structure separately from those in the marginals. By optimizing the relative weights among them, the new regularization strategy greatly relaxes the rigidness of the existing approaches. It allows a learning machine to pay special attention to places where the differences matter the most. Experiments on three real-world datasets show that the improvements are quite notable and robust compared to various benchmark domain adaptation models.

Moderately-Balanced Representation Learning for Treatment Effects with Orthogonality Information

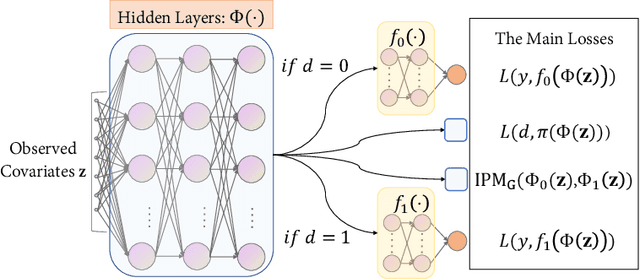
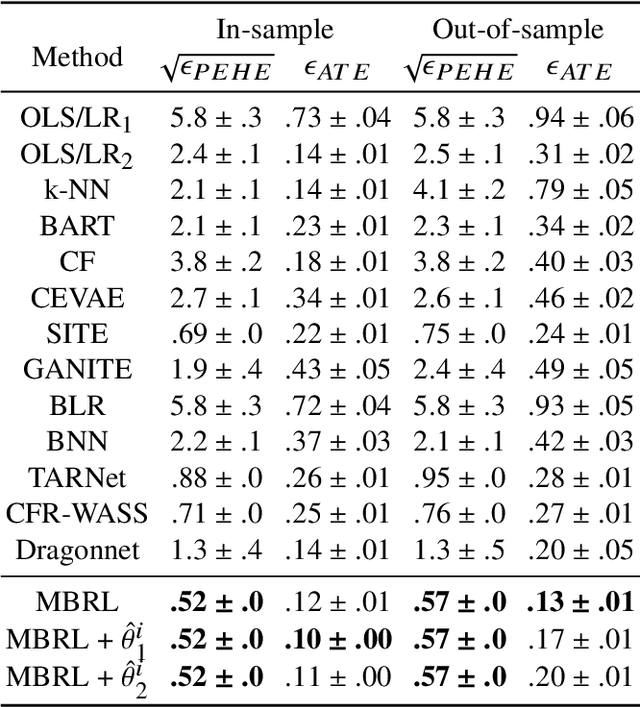
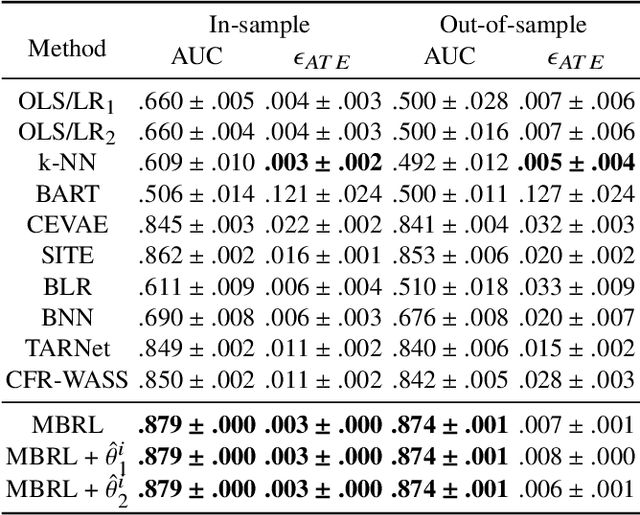
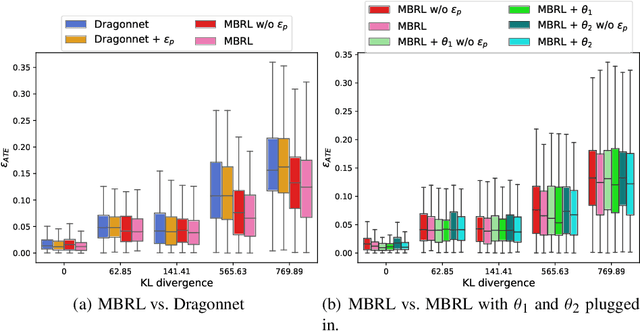
Estimating the average treatment effect (ATE) from observational data is challenging due to selection bias. Existing works mainly tackle this challenge in two ways. Some researchers propose constructing a score function that satisfies the orthogonal condition, which guarantees that the established ATE estimator is "orthogonal" to be more robust. The others explore representation learning models to achieve a balanced representation between the treated and the controlled groups. However, existing studies fail to 1) discriminate treated units from controlled ones in the representation space to avoid the over-balanced issue; 2) fully utilize the "orthogonality information". In this paper, we propose a moderately-balanced representation learning (MBRL) framework based on recent covariates balanced representation learning methods and orthogonal machine learning theory. This framework protects the representation from being over-balanced via multi-task learning. Simultaneously, MBRL incorporates the noise orthogonality information in the training and validation stages to achieve a better ATE estimation. The comprehensive experiments on benchmark and simulated datasets show the superiority and robustness of our method on treatment effect estimations compared with existing state-of-the-art methods.

Robust Causal Learning for the Estimation of Average Treatment Effects

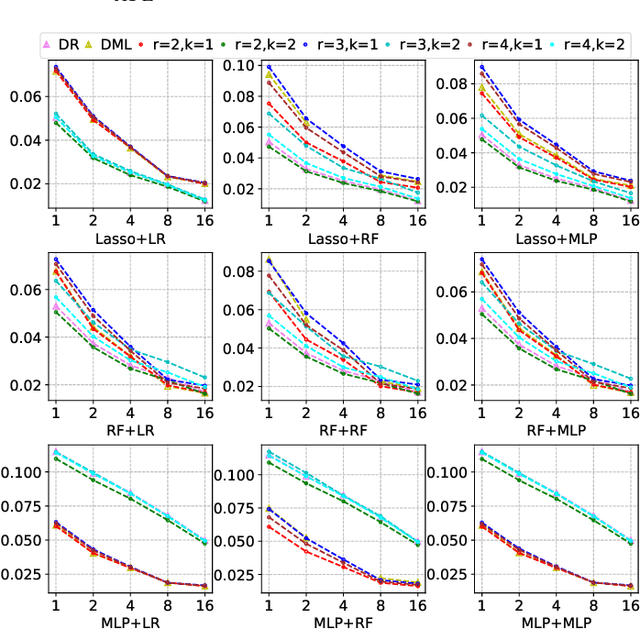
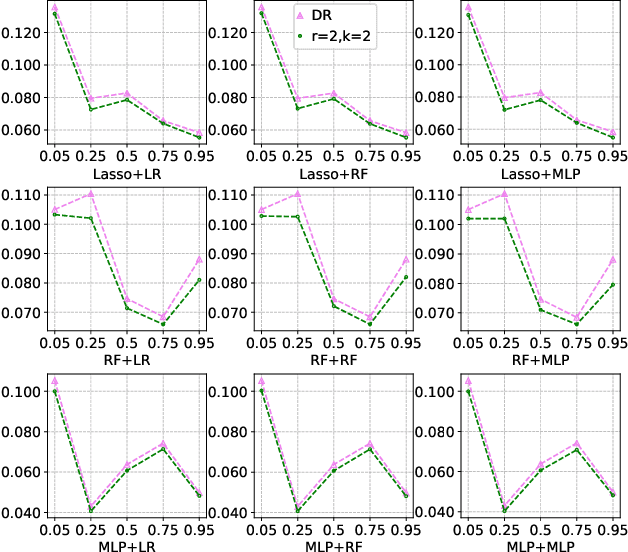
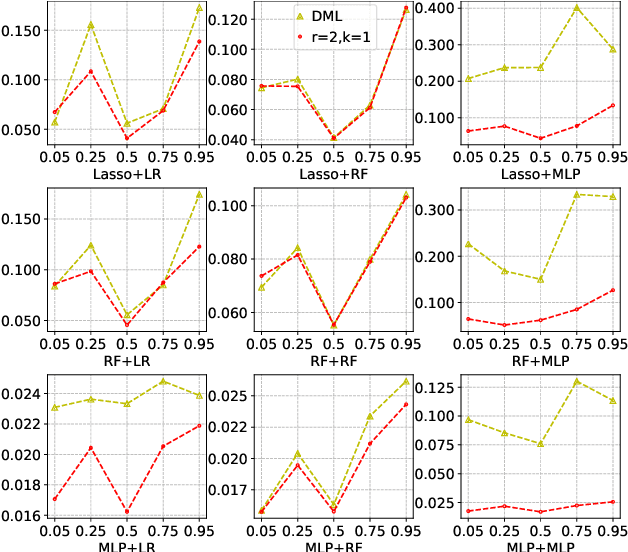
Many practical decision-making problems in economics and healthcare seek to estimate the average treatment effect (ATE) from observational data. The Double/Debiased Machine Learning (DML) is one of the prevalent methods to estimate ATE in the observational study. However, the DML estimators can suffer an error-compounding issue and even give an extreme estimate when the propensity scores are misspecified or very close to 0 or 1. Previous studies have overcome this issue through some empirical tricks such as propensity score trimming, yet none of the existing literature solves this problem from a theoretical standpoint. In this paper, we propose a Robust Causal Learning (RCL) method to offset the deficiencies of the DML estimators. Theoretically, the RCL estimators i) are as consistent and doubly robust as the DML estimators, and ii) can get rid of the error-compounding issue. Empirically, the comprehensive experiments show that i) the RCL estimators give more stable estimations of the causal parameters than the DML estimators, and ii) the RCL estimators outperform the traditional estimators and their variants when applying different machine learning models on both simulation and benchmark datasets.

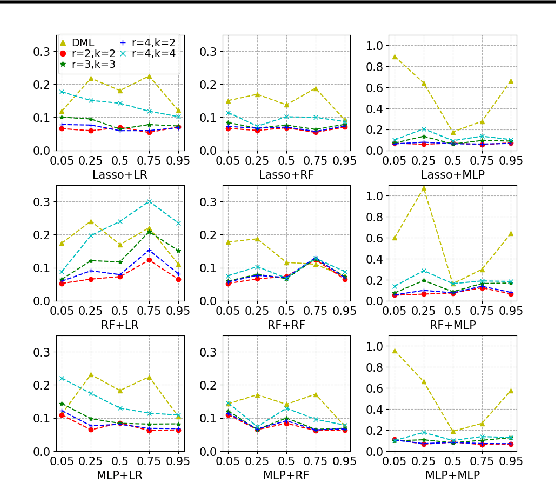
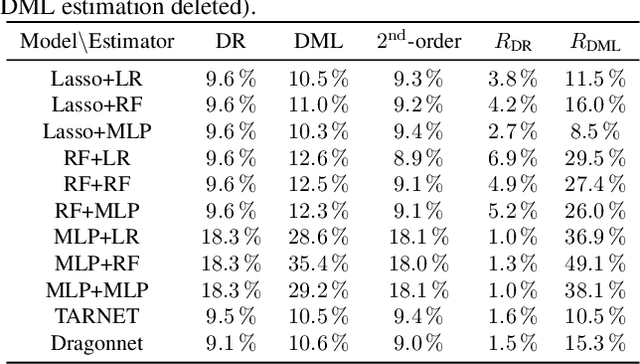
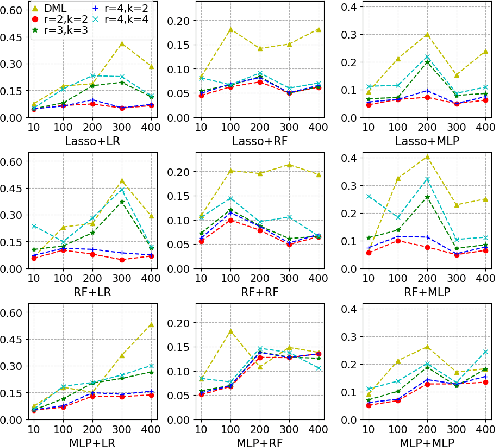
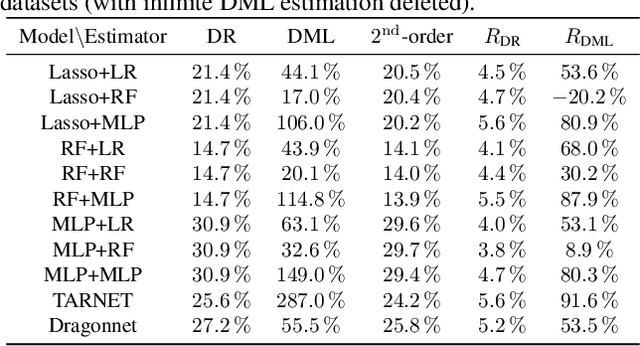
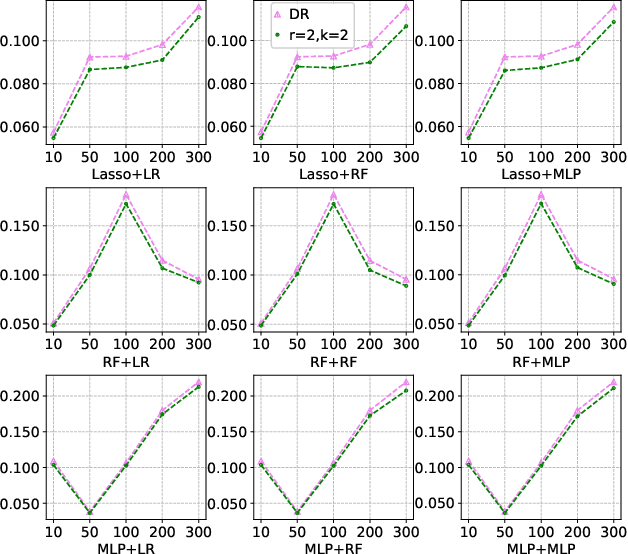
Higher-Order Orthogonal Causal Learning for Treatment Effect

Most existing studies on the double/debiased machine learning method concentrate on the causal parameter estimation recovering from the first-order orthogonal score function. In this paper, we will construct the $k^{\mathrm{th}}$-order orthogonal score function for estimating the average treatment effect (ATE) and present an algorithm that enables us to obtain the debiased estimator recovered from the score function. Such a higher-order orthogonal estimator is more robust to the misspecification of the propensity score than the first-order one does. Besides, it has the merit of being applicable with many machine learning methodologies such as Lasso, Random Forests, Neural Nets, etc. We also undergo comprehensive experiments to test the power of the estimator we construct from the score function using both the simulated datasets and the real datasets.

The Causal Learning of Retail Delinquency

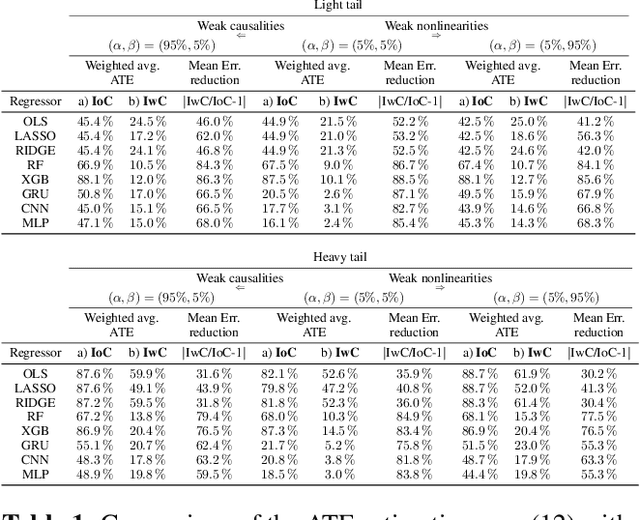
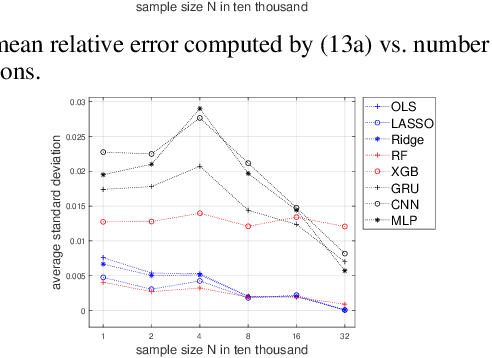
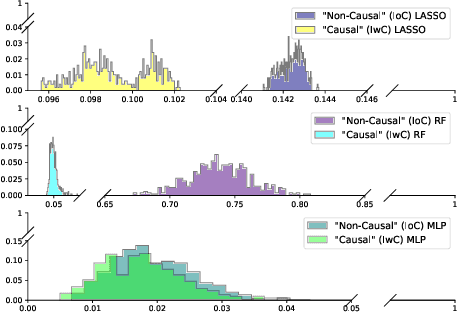
This paper focuses on the expected difference in borrower's repayment when there is a change in the lender's credit decisions. Classical estimators overlook the confounding effects and hence the estimation error can be magnificent. As such, we propose another approach to construct the estimators such that the error can be greatly reduced. The proposed estimators are shown to be unbiased, consistent, and robust through a combination of theoretical analysis and numerical testing. Moreover, we compare the power of estimating the causal quantities between the classical estimators and the proposed estimators. The comparison is tested across a wide range of models, including linear regression models, tree-based models, and neural network-based models, under different simulated datasets that exhibit different levels of causality, different degrees of nonlinearity, and different distributional properties. Most importantly, we apply our approaches to a large observational dataset provided by a global technology firm that operates in both the e-commerce and the lending business. We find that the relative reduction of estimation error is strikingly substantial if the causal effects are accounted for correctly.

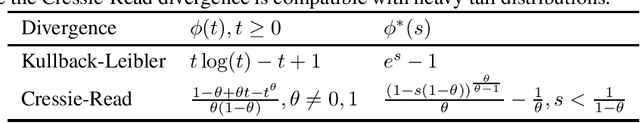
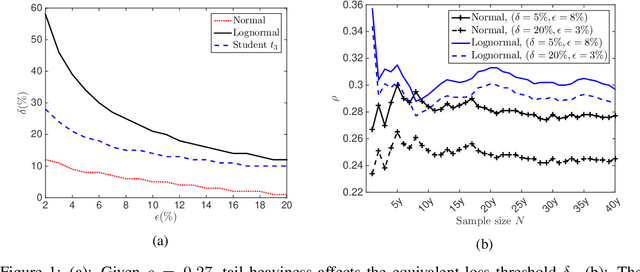
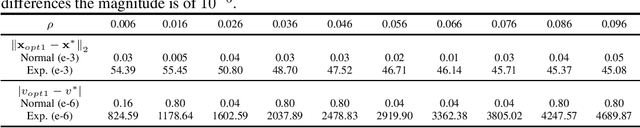
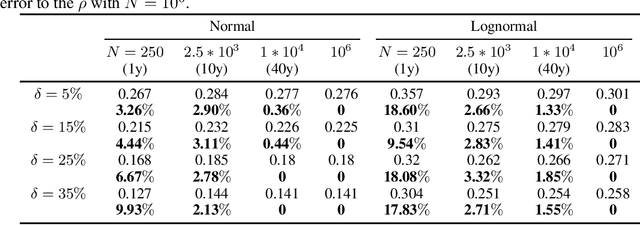
Understanding Distributional Ambiguity via Non-robust Chance Constraint

The choice of the ambiguity radius is critical when an investor uses the distributionally robust approach to address the issue that the portfolio optimization problem is sensitive to the uncertainties of the asset return distribution. It cannot be set too large because the larger the size of the ambiguity set the worse the portfolio return. It cannot be too small either; otherwise, one loses the robust protection. This tradeoff demands a financial understanding of the ambiguity set. In this paper, we propose a non-robust interpretation of the distributionally robust optimization (DRO) problem. By relating the impact of an ambiguity set to the impact of a non-robust chance constraint, our interpretation allows investors to understand the size of the ambiguity set through parameters that are directly linked to investment performance. We first show that for general $\phi$-divergences, a DRO problem is asymptotically equivalent to a class of mean-deviation problem, where the ambiguity radius controls investor's risk preference. Based on this non-robust reformulation, we then show that when a boundedness constraint is added to the investment strategy, the DRO problem can be cast as a chance-constrained optimization (CCO) problem without distributional uncertainties. If the boundedness constraint is removed, the CCO problem is shown to perform uniformly better than the DRO problem, irrespective of the radius of the ambiguity set, the choice of the divergence measure, or the tail heaviness of the center distribution. Our results apply to both the widely-used Kullback-Leibler (KL) divergence which requires the distribution of the objective function to be exponentially bounded, as well as those more general divergence measures which allow heavy tail ones such as student $t$ and lognormal distributions.