Deep into The Domain Shift: Transfer Learning through Dependence Regularization

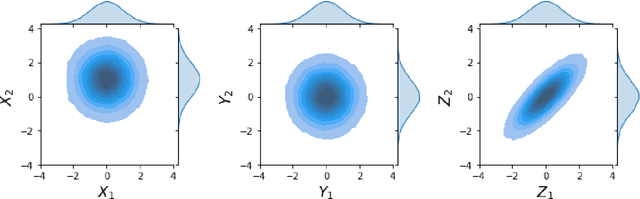
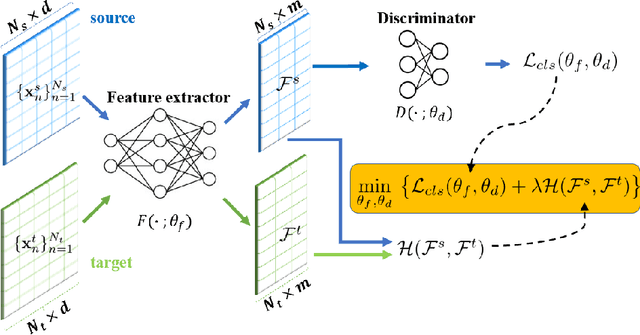
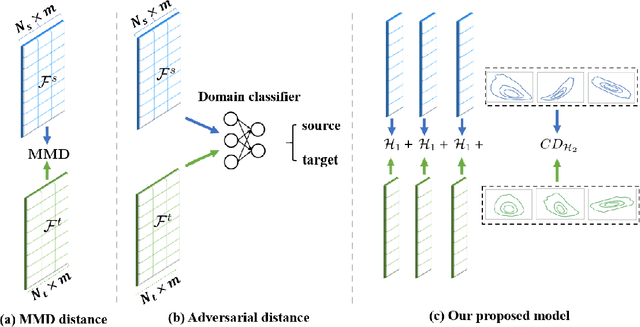
Classical Domain Adaptation methods acquire transferability by regularizing the overall distributional discrepancies between features in the source domain (labeled) and features in the target domain (unlabeled). They often do not differentiate whether the domain differences come from the marginals or the dependence structures. In many business and financial applications, the labeling function usually has different sensitivities to the changes in the marginals versus changes in the dependence structures. Measuring the overall distributional differences will not be discriminative enough in acquiring transferability. Without the needed structural resolution, the learned transfer is less optimal. This paper proposes a new domain adaptation approach in which one can measure the differences in the internal dependence structure separately from those in the marginals. By optimizing the relative weights among them, the new regularization strategy greatly relaxes the rigidness of the existing approaches. It allows a learning machine to pay special attention to places where the differences matter the most. Experiments on three real-world datasets show that the improvements are quite notable and robust compared to various benchmark domain adaptation models.

Moderately-Balanced Representation Learning for Treatment Effects with Orthogonality Information

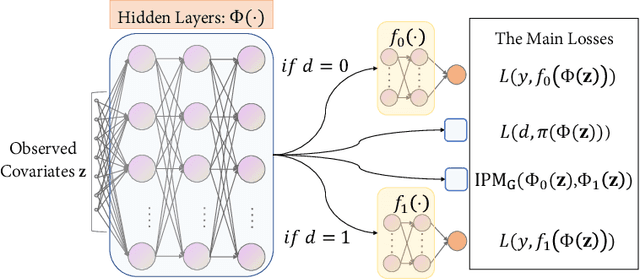
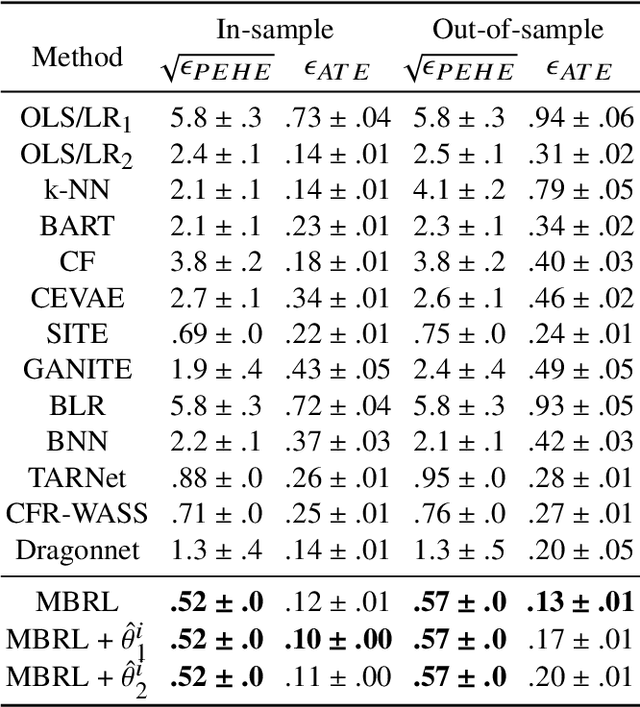
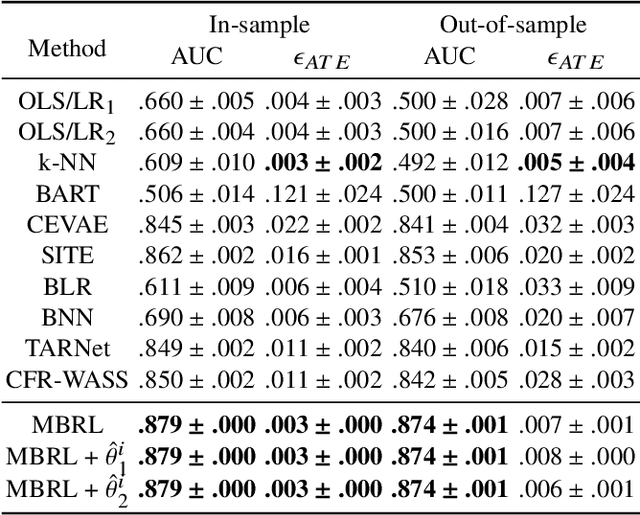
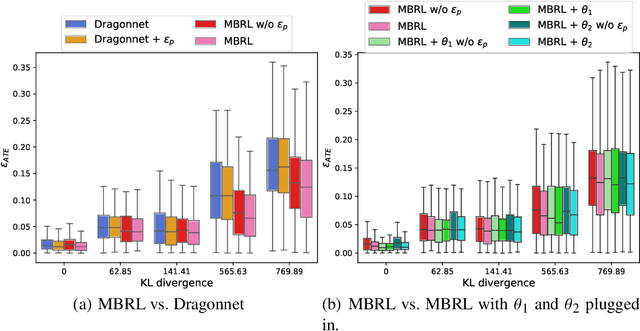
Estimating the average treatment effect (ATE) from observational data is challenging due to selection bias. Existing works mainly tackle this challenge in two ways. Some researchers propose constructing a score function that satisfies the orthogonal condition, which guarantees that the established ATE estimator is "orthogonal" to be more robust. The others explore representation learning models to achieve a balanced representation between the treated and the controlled groups. However, existing studies fail to 1) discriminate treated units from controlled ones in the representation space to avoid the over-balanced issue; 2) fully utilize the "orthogonality information". In this paper, we propose a moderately-balanced representation learning (MBRL) framework based on recent covariates balanced representation learning methods and orthogonal machine learning theory. This framework protects the representation from being over-balanced via multi-task learning. Simultaneously, MBRL incorporates the noise orthogonality information in the training and validation stages to achieve a better ATE estimation. The comprehensive experiments on benchmark and simulated datasets show the superiority and robustness of our method on treatment effect estimations compared with existing state-of-the-art methods.

Robust Causal Learning for the Estimation of Average Treatment Effects

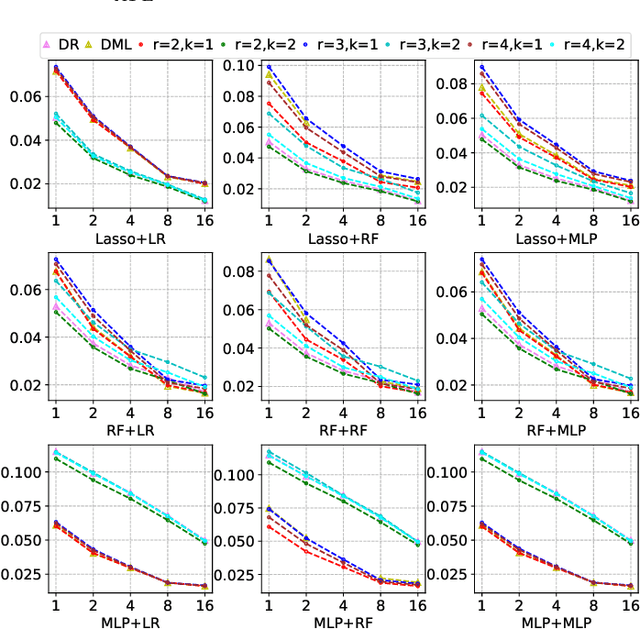
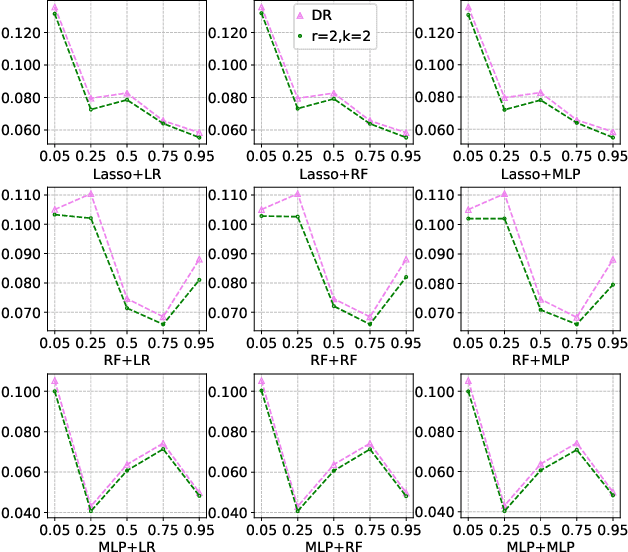
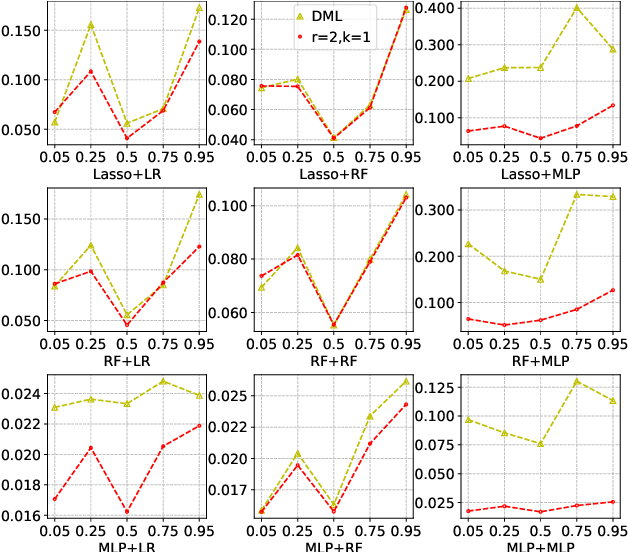
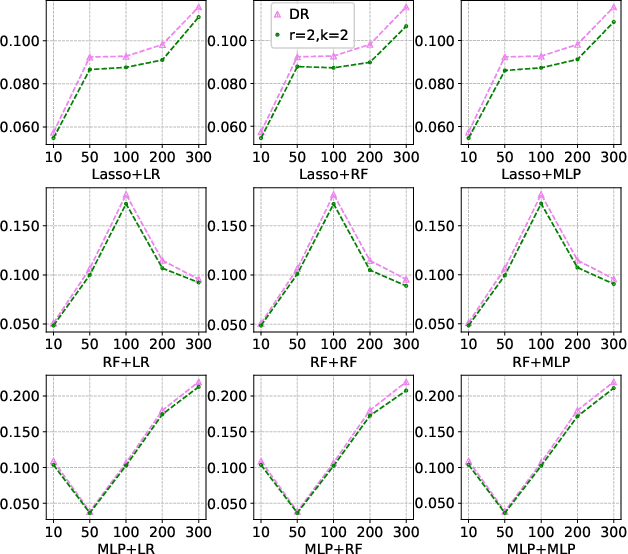
Many practical decision-making problems in economics and healthcare seek to estimate the average treatment effect (ATE) from observational data. The Double/Debiased Machine Learning (DML) is one of the prevalent methods to estimate ATE in the observational study. However, the DML estimators can suffer an error-compounding issue and even give an extreme estimate when the propensity scores are misspecified or very close to 0 or 1. Previous studies have overcome this issue through some empirical tricks such as propensity score trimming, yet none of the existing literature solves this problem from a theoretical standpoint. In this paper, we propose a Robust Causal Learning (RCL) method to offset the deficiencies of the DML estimators. Theoretically, the RCL estimators i) are as consistent and doubly robust as the DML estimators, and ii) can get rid of the error-compounding issue. Empirically, the comprehensive experiments show that i) the RCL estimators give more stable estimations of the causal parameters than the DML estimators, and ii) the RCL estimators outperform the traditional estimators and their variants when applying different machine learning models on both simulation and benchmark datasets.

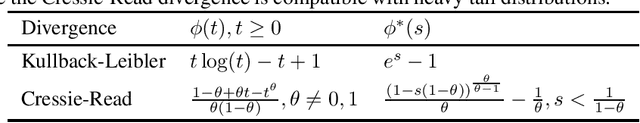
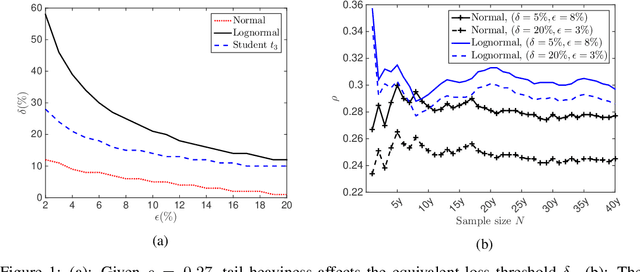
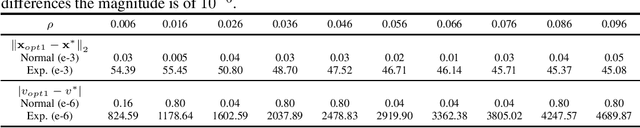
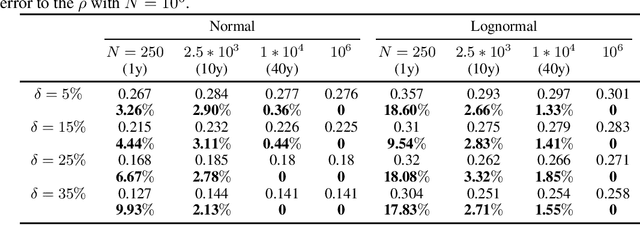
Understanding Distributional Ambiguity via Non-robust Chance Constraint

The choice of the ambiguity radius is critical when an investor uses the distributionally robust approach to address the issue that the portfolio optimization problem is sensitive to the uncertainties of the asset return distribution. It cannot be set too large because the larger the size of the ambiguity set the worse the portfolio return. It cannot be too small either; otherwise, one loses the robust protection. This tradeoff demands a financial understanding of the ambiguity set. In this paper, we propose a non-robust interpretation of the distributionally robust optimization (DRO) problem. By relating the impact of an ambiguity set to the impact of a non-robust chance constraint, our interpretation allows investors to understand the size of the ambiguity set through parameters that are directly linked to investment performance. We first show that for general $\phi$-divergences, a DRO problem is asymptotically equivalent to a class of mean-deviation problem, where the ambiguity radius controls investor's risk preference. Based on this non-robust reformulation, we then show that when a boundedness constraint is added to the investment strategy, the DRO problem can be cast as a chance-constrained optimization (CCO) problem without distributional uncertainties. If the boundedness constraint is removed, the CCO problem is shown to perform uniformly better than the DRO problem, irrespective of the radius of the ambiguity set, the choice of the divergence measure, or the tail heaviness of the center distribution. Our results apply to both the widely-used Kullback-Leibler (KL) divergence which requires the distribution of the objective function to be exponentially bounded, as well as those more general divergence measures which allow heavy tail ones such as student $t$ and lognormal distributions.