Invariant Random Forest: Tree-Based Model Solution for OOD Generalization

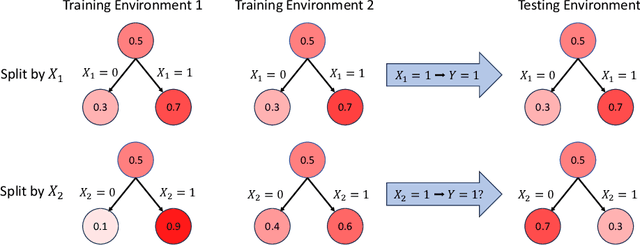
Out-Of-Distribution (OOD) generalization is an essential topic in machine learning. However, recent research is only focusing on the corresponding methods for neural networks. This paper introduces a novel and effective solution for OOD generalization of decision tree models, named Invariant Decision Tree (IDT). IDT enforces a penalty term with regard to the unstable/varying behavior of a split across different environments during the growth of the tree. Its ensemble version, the Invariant Random Forest (IRF), is constructed. Our proposed method is motivated by a theoretical result under mild conditions, and validated by numerical tests with both synthetic and real datasets. The superior performance compared to non-OOD tree models implies that considering OOD generalization for tree models is absolutely necessary and should be given more attention.

The Causal Impact of Credit Lines on Spending Distributions

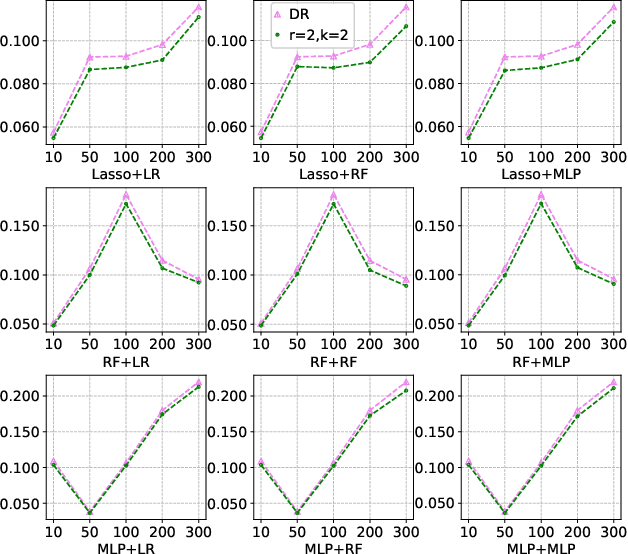
Consumer credit services offered by e-commerce platforms provide customers with convenient loan access during shopping and have the potential to stimulate sales. To understand the causal impact of credit lines on spending, previous studies have employed causal estimators, based on direct regression (DR), inverse propensity weighting (IPW), and double machine learning (DML) to estimate the treatment effect. However, these estimators do not consider the notion that an individual's spending can be understood and represented as a distribution, which captures the range and pattern of amounts spent across different orders. By disregarding the outcome as a distribution, valuable insights embedded within the outcome distribution might be overlooked. This paper develops a distribution-valued estimator framework that extends existing real-valued DR-, IPW-, and DML-based estimators to distribution-valued estimators within Rubin's causal framework. We establish their consistency and apply them to a real dataset from a large e-commerce platform. Our findings reveal that credit lines positively influence spending across all quantiles; however, as credit lines increase, consumers allocate more to luxuries (higher quantiles) than necessities (lower quantiles).

Improving Uncertainty Quantification of Variance Networks by Tree-Structured Learning

To improve uncertainty quantification of variance networks, we propose a novel tree-structured local neural network model that partitions the feature space into multiple regions based on uncertainty heterogeneity. A tree is built upon giving the training data, whose leaf nodes represent different regions where region-specific neural networks are trained to predict both the mean and the variance for quantifying uncertainty. The proposed Uncertainty-Splitting Neural Regression Tree (USNRT) employs novel splitting criteria. At each node, a neural network is trained on the full data first, and a statistical test for the residuals is conducted to find the best split, corresponding to the two sub-regions with the most significant uncertainty heterogeneity. USNRT is computationally friendly because very few leaf nodes are sufficient and pruning is unnecessary. On extensive UCI datasets, in terms of both calibration and sharpness, USNRT shows superior performance compared to some recent popular methods for variance prediction, including vanilla variance network, deep ensemble, dropout-based methods, tree-based models, etc. Through comprehensive visualization and analysis, we uncover how USNRT works and show its merits.

Ensemble Multi-Quantile: Adaptively Flexible Distribution Prediction for Uncertainty Quantification

We propose a novel, succinct, and effective approach to quantify uncertainty in machine learning. It incorporates adaptively flexible distribution prediction for $\mathbb{P}(\mathbf{y}|\mathbf{X}=x)$ in regression tasks. For predicting this conditional distribution, its quantiles of probability levels spreading the interval $(0,1)$ are boosted by additive models which are designed by us with intuitions and interpretability. We seek an adaptive balance between the structural integrity and the flexibility for $\mathbb{P}(\mathbf{y}|\mathbf{X}=x)$, while Gaussian assumption results in a lack of flexibility for real data and highly flexible approaches (e.g., estimating the quantiles separately without a distribution structure) inevitably have drawbacks and may not lead to good generalization. This ensemble multi-quantiles approach called EMQ proposed by us is totally data-driven, and can gradually depart from Gaussian and discover the optimal conditional distribution in the boosting. On extensive regression tasks from UCI datasets, we show that EMQ achieves state-of-the-art performance comparing to many recent uncertainty quantification methods including Gaussian assumption-based, Bayesian methods, quantile regression-based, and traditional tree models, under the metrics of calibration, sharpness, and tail-side calibration. Visualization results show what we actually learn from the real data and how, illustrating the necessity and the merits of such an ensemble model.

Decorr: Environment Partitioning for Invariant Learning and OOD Generalization

Invariant learning methods try to find an invariant predictor across several environments and have become popular in OOD generalization. However, in situations where environments do not naturally exist in the data, they have to be decided by practitioners manually. Environment partitioning, which splits the whole training dataset into environments by algorithms, will significantly influence the performance of invariant learning and has been left undiscussed. A good environment partitioning method can bring invariant learning to applications with more general settings and improve its performance. We propose to split the dataset into several environments by finding low-correlated data subsets. Theoretical interpretations and algorithm details are both introduced in the paper. Through experiments on both synthetic and real data, we show that our Decorr method can achieve outstanding performance, while some other partitioning methods may lead to bad, even below-ERM results using the same training scheme of IRM.

Robust Causal Learning for the Estimation of Average Treatment Effects

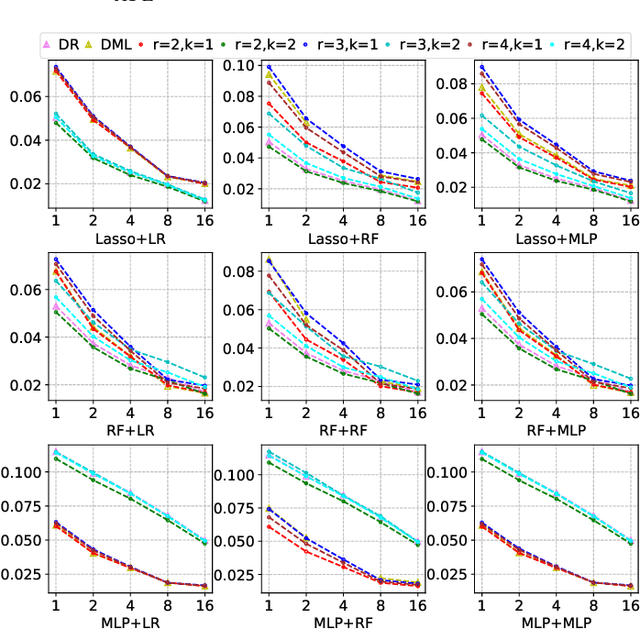
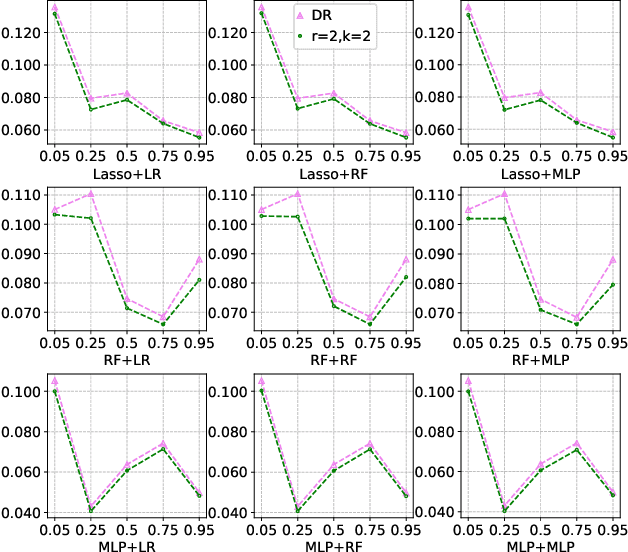
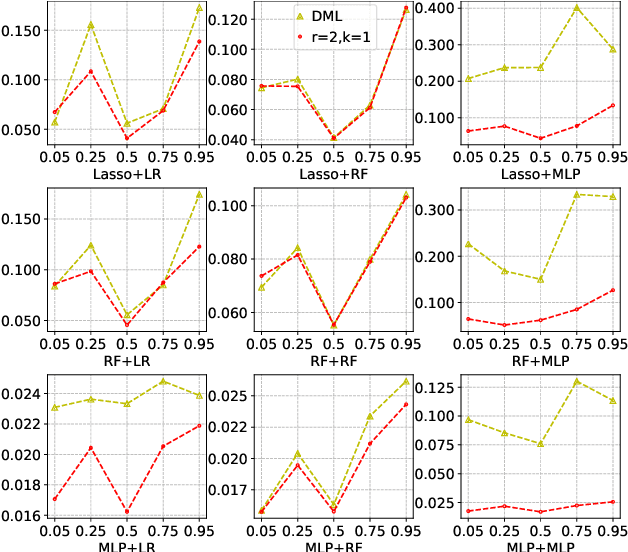
Many practical decision-making problems in economics and healthcare seek to estimate the average treatment effect (ATE) from observational data. The Double/Debiased Machine Learning (DML) is one of the prevalent methods to estimate ATE in the observational study. However, the DML estimators can suffer an error-compounding issue and even give an extreme estimate when the propensity scores are misspecified or very close to 0 or 1. Previous studies have overcome this issue through some empirical tricks such as propensity score trimming, yet none of the existing literature solves this problem from a theoretical standpoint. In this paper, we propose a Robust Causal Learning (RCL) method to offset the deficiencies of the DML estimators. Theoretically, the RCL estimators i) are as consistent and doubly robust as the DML estimators, and ii) can get rid of the error-compounding issue. Empirically, the comprehensive experiments show that i) the RCL estimators give more stable estimations of the causal parameters than the DML estimators, and ii) the RCL estimators outperform the traditional estimators and their variants when applying different machine learning models on both simulation and benchmark datasets.

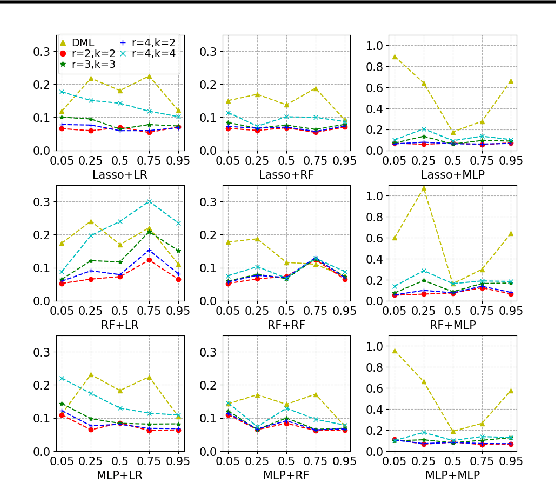
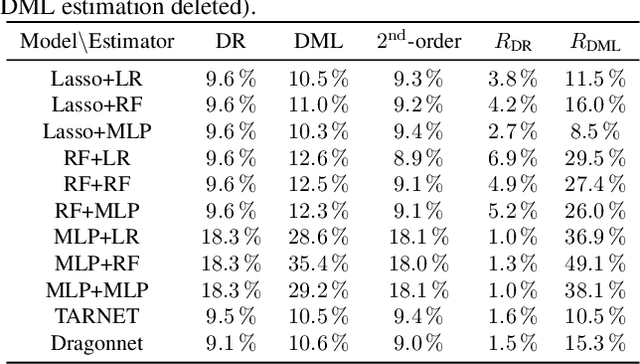
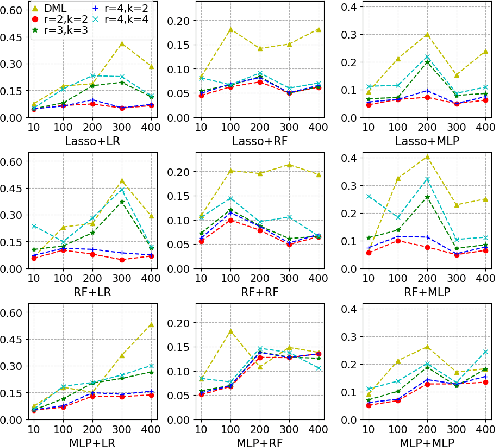
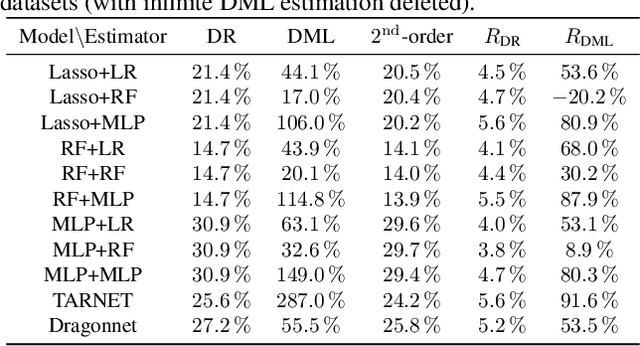
Higher-Order Orthogonal Causal Learning for Treatment Effect

Most existing studies on the double/debiased machine learning method concentrate on the causal parameter estimation recovering from the first-order orthogonal score function. In this paper, we will construct the $k^{\mathrm{th}}$-order orthogonal score function for estimating the average treatment effect (ATE) and present an algorithm that enables us to obtain the debiased estimator recovered from the score function. Such a higher-order orthogonal estimator is more robust to the misspecification of the propensity score than the first-order one does. Besides, it has the merit of being applicable with many machine learning methodologies such as Lasso, Random Forests, Neural Nets, etc. We also undergo comprehensive experiments to test the power of the estimator we construct from the score function using both the simulated datasets and the real datasets.

The Causal Learning of Retail Delinquency

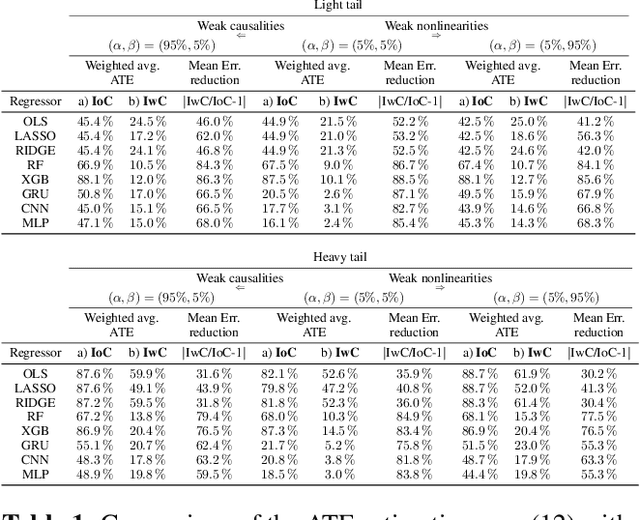
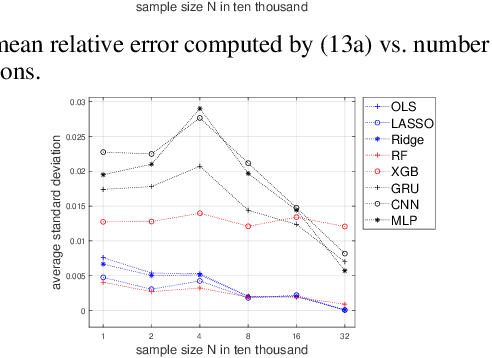
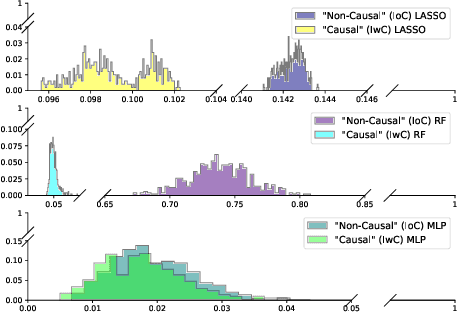
This paper focuses on the expected difference in borrower's repayment when there is a change in the lender's credit decisions. Classical estimators overlook the confounding effects and hence the estimation error can be magnificent. As such, we propose another approach to construct the estimators such that the error can be greatly reduced. The proposed estimators are shown to be unbiased, consistent, and robust through a combination of theoretical analysis and numerical testing. Moreover, we compare the power of estimating the causal quantities between the classical estimators and the proposed estimators. The comparison is tested across a wide range of models, including linear regression models, tree-based models, and neural network-based models, under different simulated datasets that exhibit different levels of causality, different degrees of nonlinearity, and different distributional properties. Most importantly, we apply our approaches to a large observational dataset provided by a global technology firm that operates in both the e-commerce and the lending business. We find that the relative reduction of estimation error is strikingly substantial if the causal effects are accounted for correctly.

Generative Learning of Heterogeneous Tail Dependence

We propose a multivariate generative model to capture the complex dependence structure often encountered in business and financial data. Our model features heterogeneous and asymmetric tail dependence between all pairs of individual dimensions while also allowing heterogeneity and asymmetry in the tails of the marginals. A significant merit of our model structure is that it is not prone to error propagation in the parameter estimation process, hence very scalable, as the dimensions of datasets grow large. However, the likelihood methods are infeasible for parameter estimation in our case due to the lack of a closed-form density function. Instead, we devise a novel moment learning algorithm to learn the parameters. To demonstrate the effectiveness of the model and its estimator, we test them on simulated as well as real-world datasets. Results show that this framework gives better finite-sample performance compared to the copula-based benchmarks as well as recent similar models.

Parsimonious Quantile Regression of Financial Asset Tail Dynamics via Sequential Learning

We propose a parsimonious quantile regression framework to learn the dynamic tail behaviors of financial asset returns. Our model captures well both the time-varying characteristic and the asymmetrical heavy-tail property of financial time series. It combines the merits of a popular sequential neural network model, i.e., LSTM, with a novel parametric quantile function that we construct to represent the conditional distribution of asset returns. Our model also captures individually the serial dependences of higher moments, rather than just the volatility. Across a wide range of asset classes, the out-of-sample forecasts of conditional quantiles or VaR of our model outperform the GARCH family. Further, the proposed approach does not suffer from the issue of quantile crossing, nor does it expose to the ill-posedness comparing to the parametric probability density function approach.