Understanding Distributional Ambiguity via Non-robust Chance Constraint

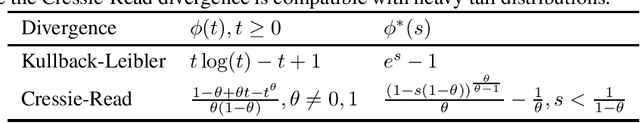
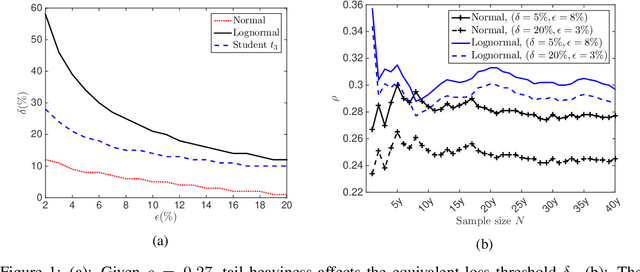
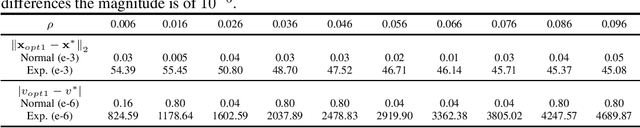
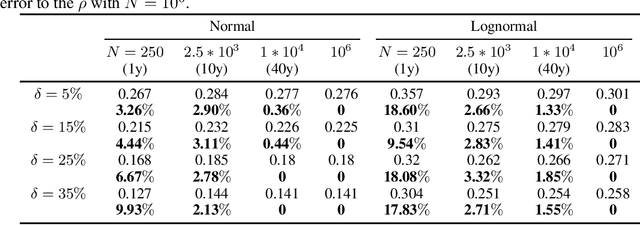
The choice of the ambiguity radius is critical when an investor uses the distributionally robust approach to address the issue that the portfolio optimization problem is sensitive to the uncertainties of the asset return distribution. It cannot be set too large because the larger the size of the ambiguity set the worse the portfolio return. It cannot be too small either; otherwise, one loses the robust protection. This tradeoff demands a financial understanding of the ambiguity set. In this paper, we propose a non-robust interpretation of the distributionally robust optimization (DRO) problem. By relating the impact of an ambiguity set to the impact of a non-robust chance constraint, our interpretation allows investors to understand the size of the ambiguity set through parameters that are directly linked to investment performance. We first show that for general $\phi$-divergences, a DRO problem is asymptotically equivalent to a class of mean-deviation problem, where the ambiguity radius controls investor's risk preference. Based on this non-robust reformulation, we then show that when a boundedness constraint is added to the investment strategy, the DRO problem can be cast as a chance-constrained optimization (CCO) problem without distributional uncertainties. If the boundedness constraint is removed, the CCO problem is shown to perform uniformly better than the DRO problem, irrespective of the radius of the ambiguity set, the choice of the divergence measure, or the tail heaviness of the center distribution. Our results apply to both the widely-used Kullback-Leibler (KL) divergence which requires the distribution of the objective function to be exponentially bounded, as well as those more general divergence measures which allow heavy tail ones such as student $t$ and lognormal distributions.