funOCLUST: Clustering Functional Data with Outliers

Functional data present unique challenges for clustering due to their infinite-dimensional nature and potential sensitivity to outliers. An extension of the OCLUST algorithm to the functional setting is proposed to address these issues. The approach leverages the OCLUST framework, creating a robust method to cluster curves and trim outliers. The methodology is evaluated on both simulated and real-world functional datasets, demonstrating strong performance in clustering and outlier identification.

Depth-Based Local Center Clustering: A Framework for Handling Different Clustering Scenarios

Cluster analysis, or clustering, plays a crucial role across numerous scientific and engineering domains. Despite the wealth of clustering methods proposed over the past decades, each method is typically designed for specific scenarios and presents certain limitations in practical applications. In this paper, we propose depth-based local center clustering (DLCC). This novel method makes use of data depth, which is known to produce a center-outward ordering of sample points in a multivariate space. However, data depth typically fails to capture the multimodal characteristics of {data}, something of the utmost importance in the context of clustering. To overcome this, DLCC makes use of a local version of data depth that is based on subsets of {data}. From this, local centers can be identified as well as clusters of varying shapes. Furthermore, we propose a new internal metric based on density-based clustering to evaluate clustering performance on {non-convex clusters}. Overall, DLCC is a flexible clustering approach that seems to overcome some limitations of traditional clustering methods, thereby enhancing data analysis capabilities across a wide range of application scenarios.

Keep It Light! Simplifying Image Clustering Via Text-Free Adapters

Many competitive clustering pipelines have a multi-modal design, leveraging large language models (LLMs) or other text encoders, and text-image pairs, which are often unavailable in real-world downstream applications. Additionally, such frameworks are generally complicated to train and require substantial computational resources, making widespread adoption challenging. In this work, we show that in deep clustering, competitive performance with more complex state-of-the-art methods can be achieved using a text-free and highly simplified training pipeline. In particular, our approach, Simple Clustering via Pre-trained models (SCP), trains only a small cluster head while leveraging pre-trained vision model feature representations and positive data pairs. Experiments on benchmark datasets including CIFAR-10, CIFAR-20, CIFAR-100, STL-10, ImageNet-10, and ImageNet-Dogs, demonstrate that SCP achieves highly competitive performance. Furthermore, we provide a theoretical result explaining why, at least under ideal conditions, additional text-based embeddings may not be necessary to achieve strong clustering performance in vision.

An EM Gradient Algorithm for Mixture Models with Components Derived from the Manly Transformation

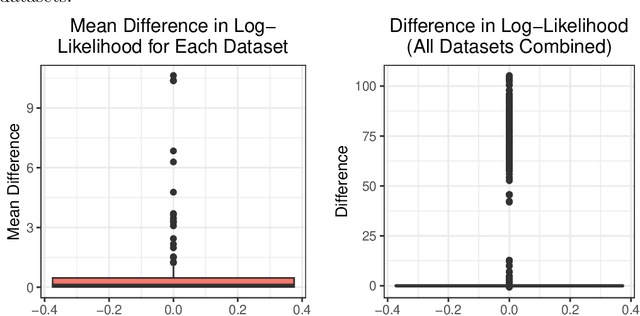
Zhu and Melnykov (2018) develop a model to fit mixture models when the components are derived from the Manly transformation. Their EM algorithm utilizes Nelder-Mead optimization in the M-step to update the skew parameter, $\boldsymbol{\lambda}_g$. An alternative EM gradient algorithm is proposed, using one step of Newton's method, when initial estimates for the model parameters are good.

Finite Mixtures of Multivariate Poisson-Log Normal Factor Analyzers for Clustering Count Data

A mixture of multivariate Poisson-log normal factor analyzers is introduced by imposing constraints on the covariance matrix, which resulted in flexible models for clustering purposes. In particular, a class of eight parsimonious mixture models based on the mixtures of factor analyzers model are introduced. Variational Gaussian approximation is used for parameter estimation, and information criteria are used for model selection. The proposed models are explored in the context of clustering discrete data arising from RNA sequencing studies. Using real and simulated data, the models are shown to give favourable clustering performance. The GitHub R package for this work is available at https://github.com/anjalisilva/mixMPLNFA and is released under the open-source MIT license.

Clustering Three-Way Data with Outliers

Matrix-variate distributions are a recent addition to the model-based clustering field, thereby making it possible to analyze data in matrix form with complex structure such as images and time series. Due to its recent appearance, there is limited literature on matrix-variate data, with even less on dealing with outliers in these models. An approach for clustering matrix-variate normal data with outliers is discussed. The approach, which uses the distribution of subset log-likelihoods, extends the OCLUST algorithm to matrix-variate normal data and uses an iterative approach to detect and trim outliers.

Clustering Higher Order Data: Finite Mixtures of Multidimensional Arrays

An approach for clustering multi-way data is introduced based on a finite mixture of multidimensional arrays. Attention to the use of multidimensional arrays for clustering has thus far been limited to two-dimensional arrays, i.e., matrices or order-two tensors. Accordingly, this is the first paper to develop an approach for clustering d-dimensional arrays for d>2 or, in other words, for clustering using order-d tensors.

Using Subset Log-Likelihoods to Trim Outliers in Gaussian Mixture Models

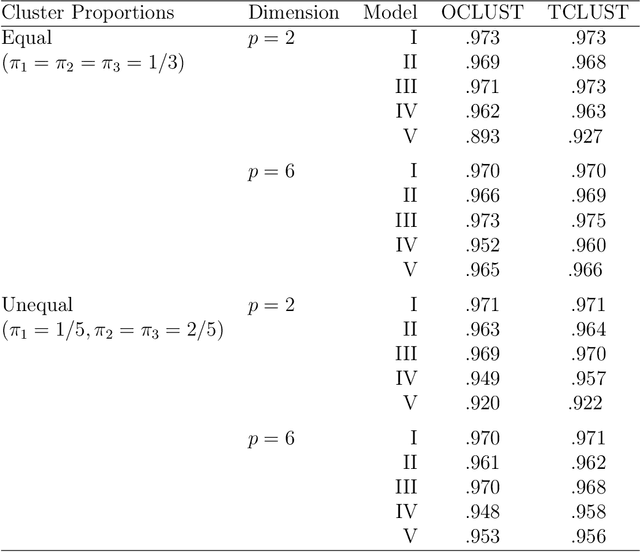
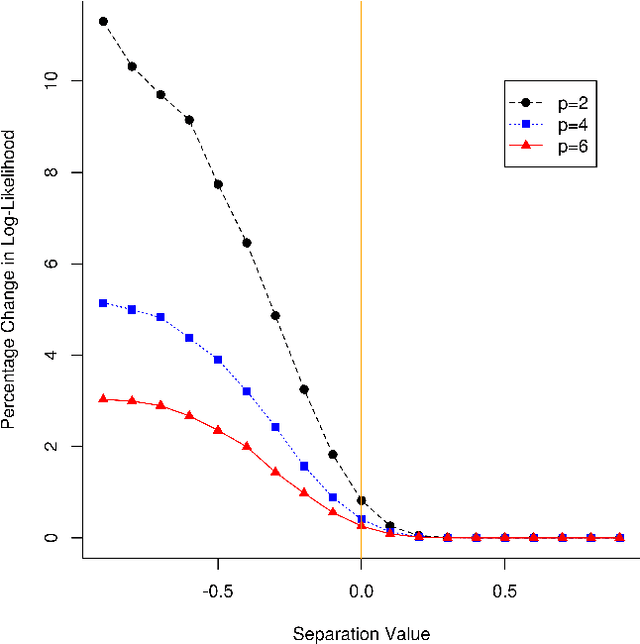
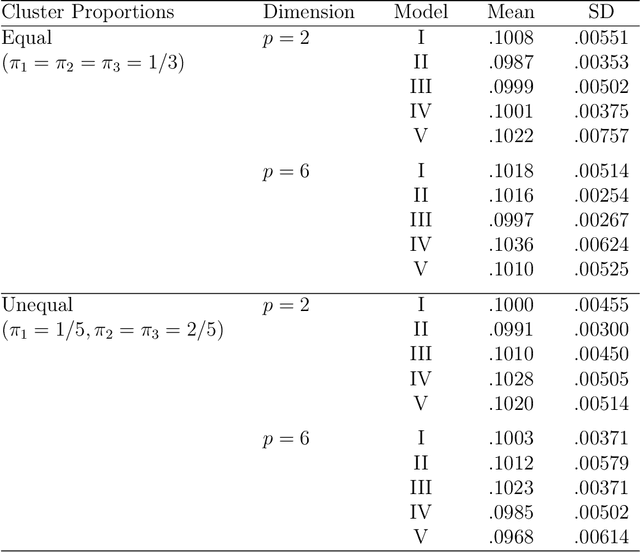
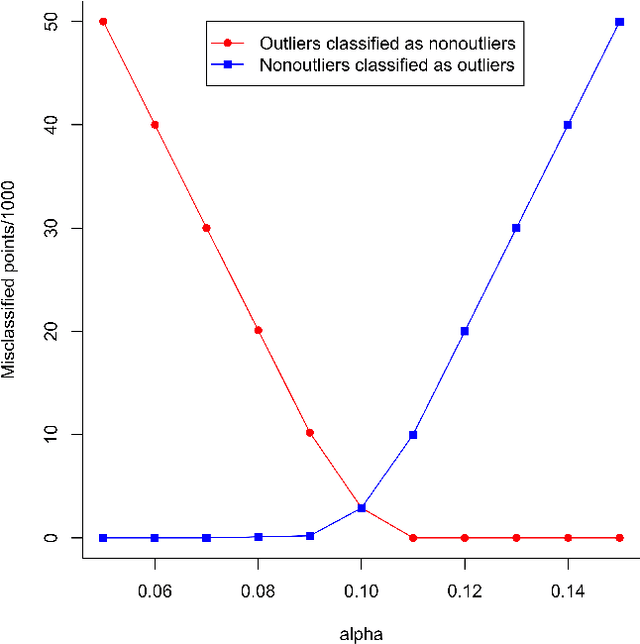
Mixtures of Gaussian distributions are a popular choice in model-based clustering. Outliers can affect parameters estimation and, as such, must be accounted for. Algorithms such as TCLUST discern the most likely outliers, but only when the proportion of outlying points is known \textit{a priori}. It is proved that, for a finite Gaussian mixture model, the log-likelihoods of the subset models are beta-distributed. An algorithm is then proposed that predicts the proportion of outliers by measuring the adherence of a set of subset log-likelihoods to a beta reference distribution. This algorithm removes the least likely points, which are deemed outliers, until model assumptions are met.

Flexible Clustering with a Sparse Mixture of Generalized Hyperbolic Distributions

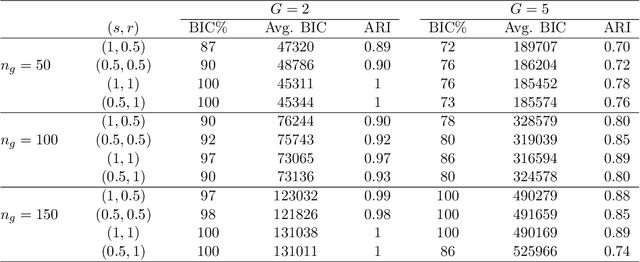
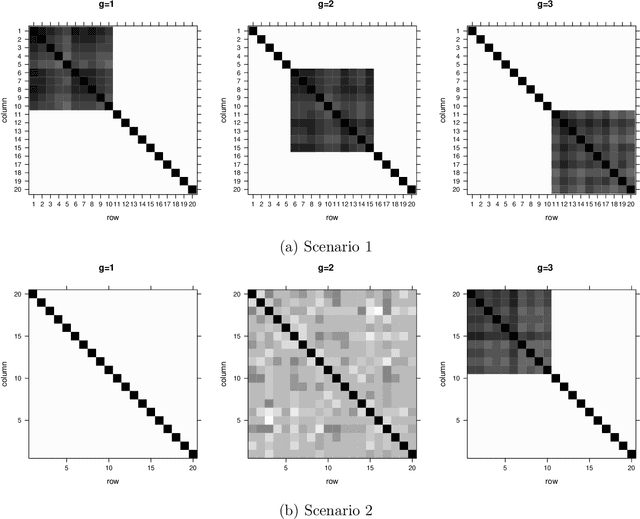
Robust clustering of high-dimensional data is an important topic because, in many practical situations, real data sets are heavy-tailed and/or asymmetric. Moreover, traditional model-based clustering often fails for high dimensional data due to the number of free covariance parameters. A parametrization of the component scale matrices for the mixture of generalized hyperbolic distributions is proposed by including a penalty term in the likelihood constraining the parameters resulting in a flexible model for high dimensional data and a meaningful interpretation. An analytically feasible EM algorithm is developed by placing a gamma-Lasso penalty constraining the concentration matrix. The proposed methodology is investigated through simulation studies and two real data sets.

Clustering Discrete Valued Time Series

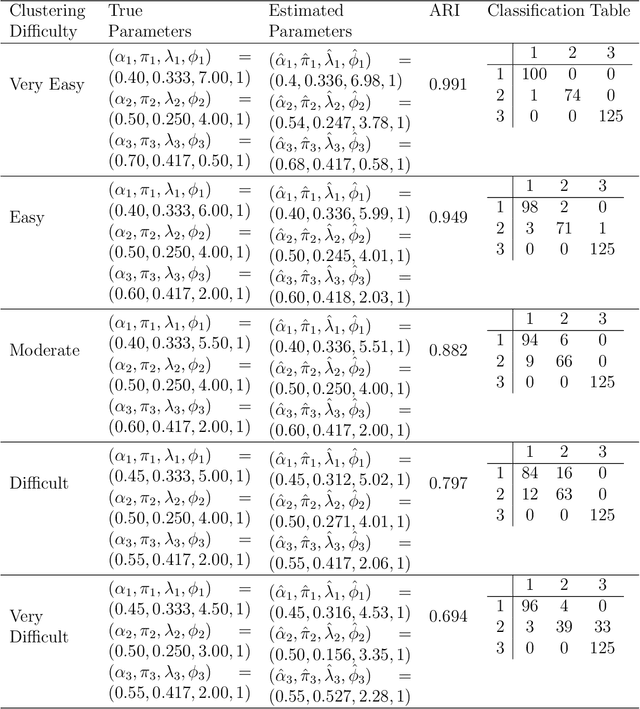
There is a need for the development of models that are able to account for discreteness in data, along with its time series properties and correlation. Our focus falls on INteger-valued AutoRegressive (INAR) type models. The INAR type models can be used in conjunction with existing model-based clustering techniques to cluster discrete valued time series data. With the use of a finite mixture model, several existing techniques such as the selection of the number of clusters, estimation using expectation-maximization and model selection are applicable. The proposed model is then demonstrated on real data to illustrate its clustering applications.