Flexible Clustering with a Sparse Mixture of Generalized Hyperbolic Distributions
Paper and Code
Mar 12, 2019
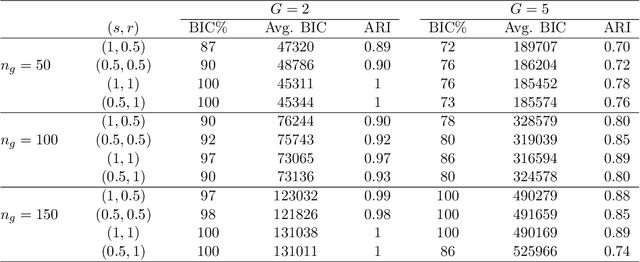
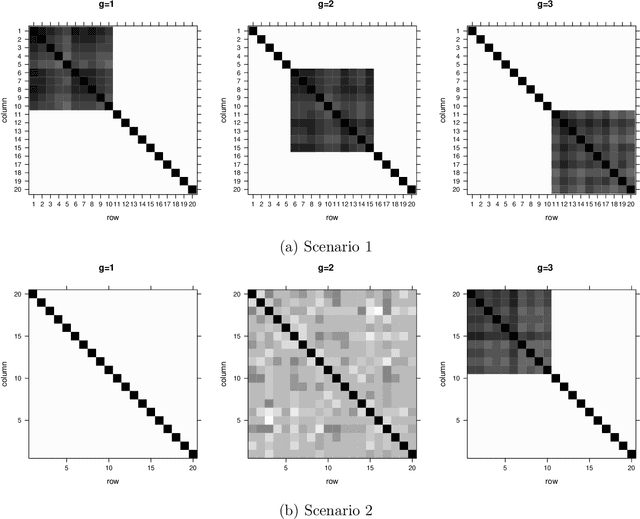

Robust clustering of high-dimensional data is an important topic because, in many practical situations, real data sets are heavy-tailed and/or asymmetric. Moreover, traditional model-based clustering often fails for high dimensional data due to the number of free covariance parameters. A parametrization of the component scale matrices for the mixture of generalized hyperbolic distributions is proposed by including a penalty term in the likelihood constraining the parameters resulting in a flexible model for high dimensional data and a meaningful interpretation. An analytically feasible EM algorithm is developed by placing a gamma-Lasso penalty constraining the concentration matrix. The proposed methodology is investigated through simulation studies and two real data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge