Flexible Clustering with a Sparse Mixture of Generalized Hyperbolic Distributions

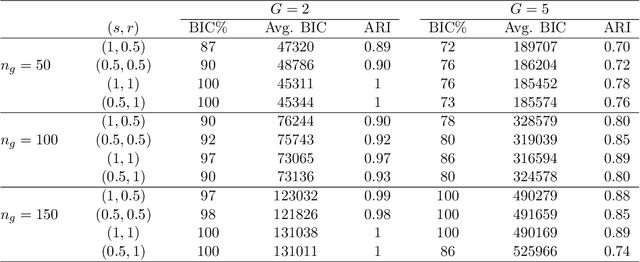
Robust clustering of high-dimensional data is an important topic because, in many practical situations, real data sets are heavy-tailed and/or asymmetric. Moreover, traditional model-based clustering often fails for high dimensional data due to the number of free covariance parameters. A parametrization of the component scale matrices for the mixture of generalized hyperbolic distributions is proposed by including a penalty term in the likelihood constraining the parameters resulting in a flexible model for high dimensional data and a meaningful interpretation. An analytically feasible EM algorithm is developed by placing a gamma-Lasso penalty constraining the concentration matrix. The proposed methodology is investigated through simulation studies and two real data sets.

A Mixture of Matrix Variate Bilinear Factor Analyzers

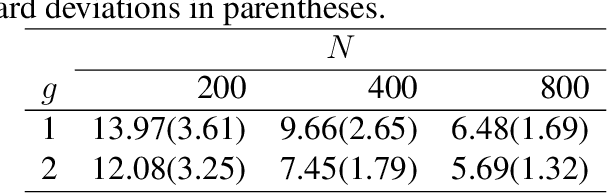
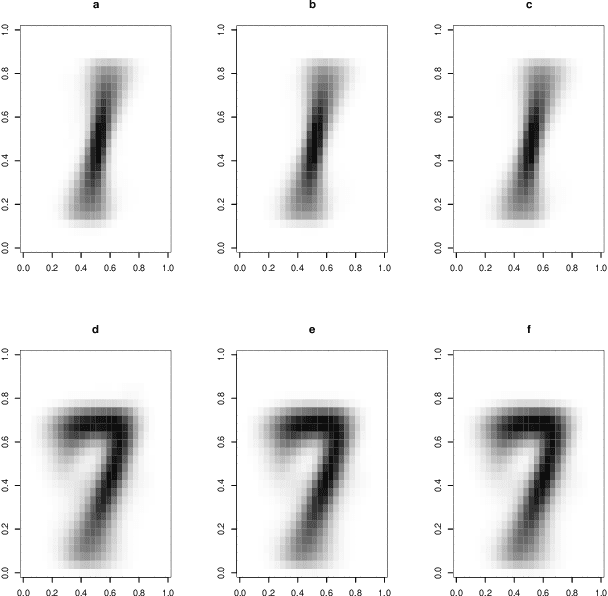
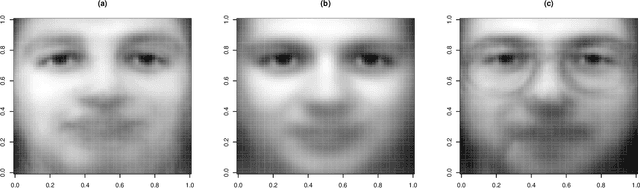
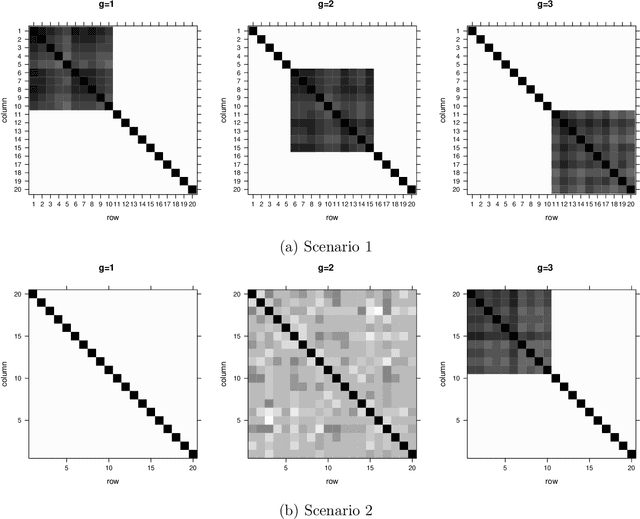
Over the years data has become increasingly higher dimensional, which has prompted an increased need for dimension reduction techniques. This is perhaps especially true for clustering (unsupervised classification) as well as semi-supervised and supervised classification. Although dimension reduction in the area of clustering for multivariate data has been quite thoroughly discussed within the literature, there is relatively little work in the area of three-way, or matrix variate, data. Herein, we develop a mixture of matrix variate bilinear factor analyzers (MMVBFA) model for use in clustering high-dimensional matrix variate data. This work can be considered both the first matrix variate bilinear factor analysis model as well as the first MMVBFA model. Parameter estimation is discussed, and the MMVBFA model is illustrated using simulated and real data.

Mixtures of Skewed Matrix Variate Bilinear Factor Analyzers

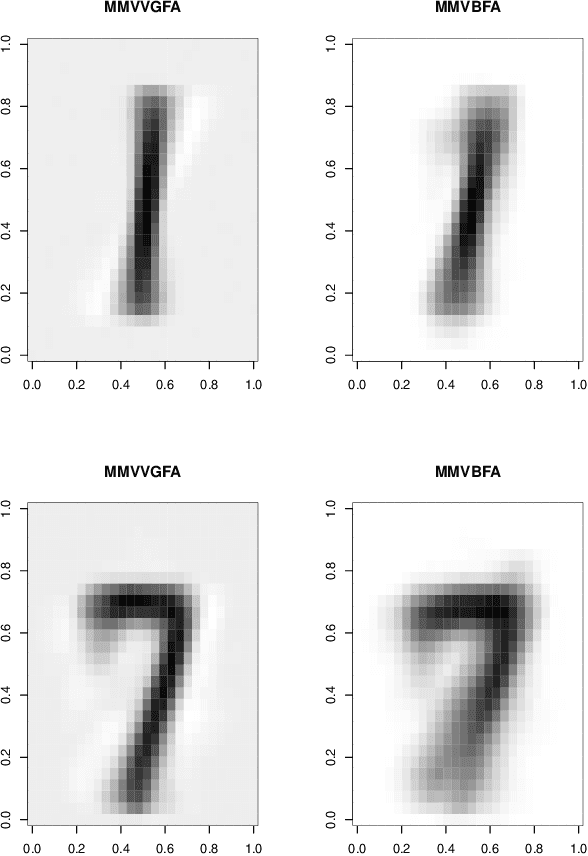
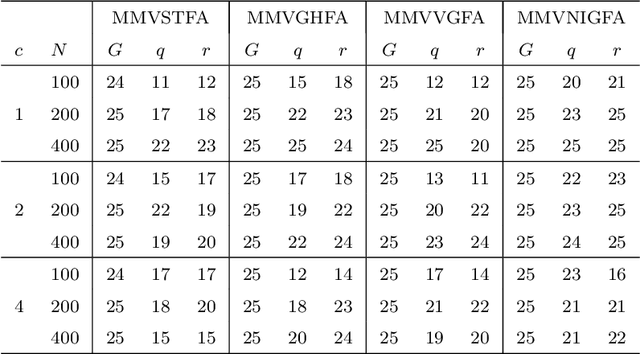
Clustering is the process of finding and analyzing underlying group structures in data. In recent years, data as become increasingly higher dimensional and therefore an increased need for dimension reduction techniques for use in clustering. Although such techniques are firmly established in the literature for multivariate data, there is a relative paucity in the area of matrix variate or three way data. Furthermore, these few methods all assume matrix variate normality which is not always sensible if skewness is present. We propose a mixture of bilinear factor analyzers model using four skewed matrix variate distributions, namely the matrix variate skew-t, generalized hyperbolic, variance gamma and normal inverse Gaussian distributions.

Clustering and Semi-Supervised Classification for Clickstream Data via Mixture Models

Finite mixture models have been used for unsupervised learning for over 60 years, and their use within the semi-supervised paradigm is becoming more commonplace. Clickstream data is one of the various emerging data types that demands particular attention because there is a notable paucity of statistical learning approaches currently available. A mixture of first order continuous time Markov models is introduced for unsupervised and semi-supervised learning of clickstream data. This approach assumes continuous time, which distinguishes it from existing mixture model-based approaches; practically, this allows account to be taken of the amount of time each user spends on each website. The approach is evaluated, and compared to the discrete time approach, using simulated and real data.