An EM Gradient Algorithm for Mixture Models with Components Derived from the Manly Transformation

Zhu and Melnykov (2018) develop a model to fit mixture models when the components are derived from the Manly transformation. Their EM algorithm utilizes Nelder-Mead optimization in the M-step to update the skew parameter, $\boldsymbol{\lambda}_g$. An alternative EM gradient algorithm is proposed, using one step of Newton's method, when initial estimates for the model parameters are good.

Clustering Three-Way Data with Outliers

Matrix-variate distributions are a recent addition to the model-based clustering field, thereby making it possible to analyze data in matrix form with complex structure such as images and time series. Due to its recent appearance, there is limited literature on matrix-variate data, with even less on dealing with outliers in these models. An approach for clustering matrix-variate normal data with outliers is discussed. The approach, which uses the distribution of subset log-likelihoods, extends the OCLUST algorithm to matrix-variate normal data and uses an iterative approach to detect and trim outliers.

Using Subset Log-Likelihoods to Trim Outliers in Gaussian Mixture Models

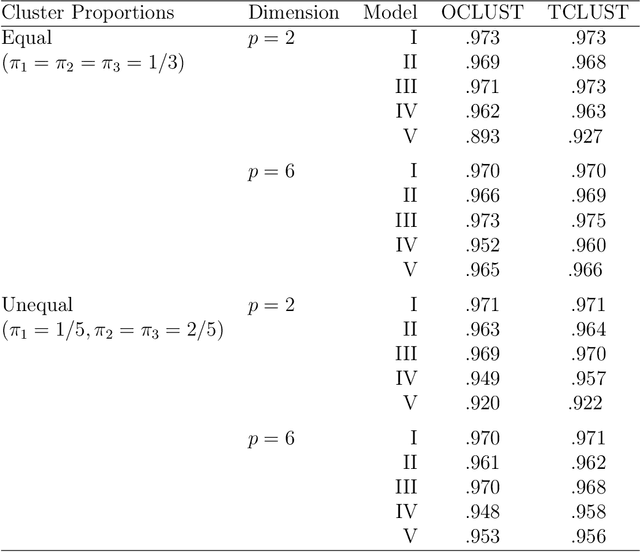
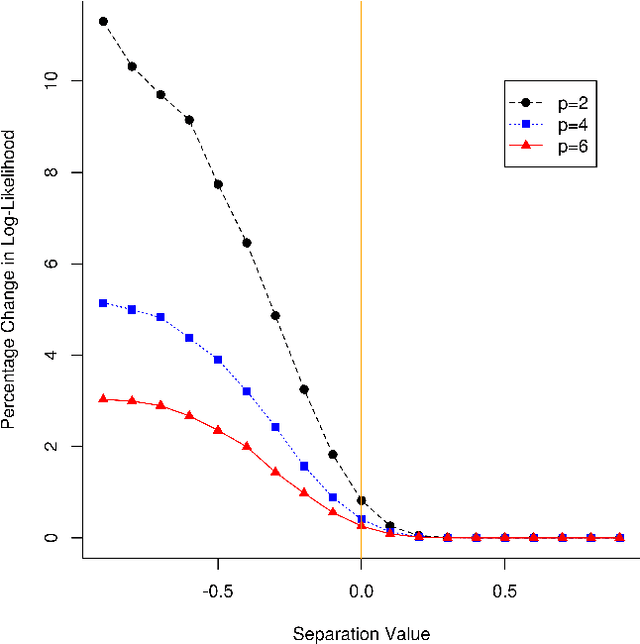
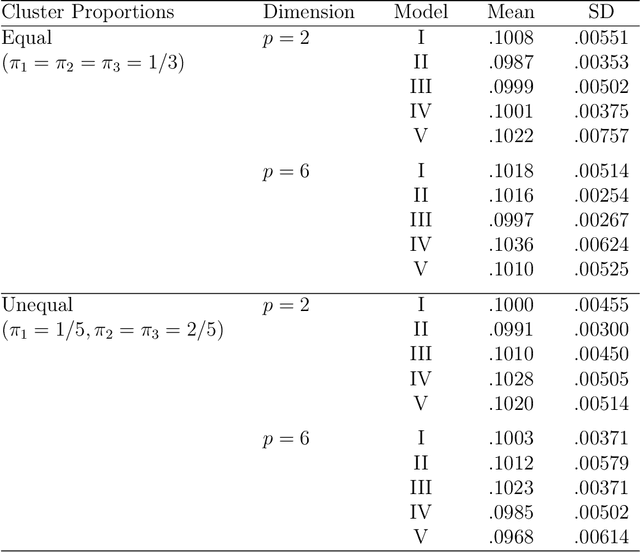
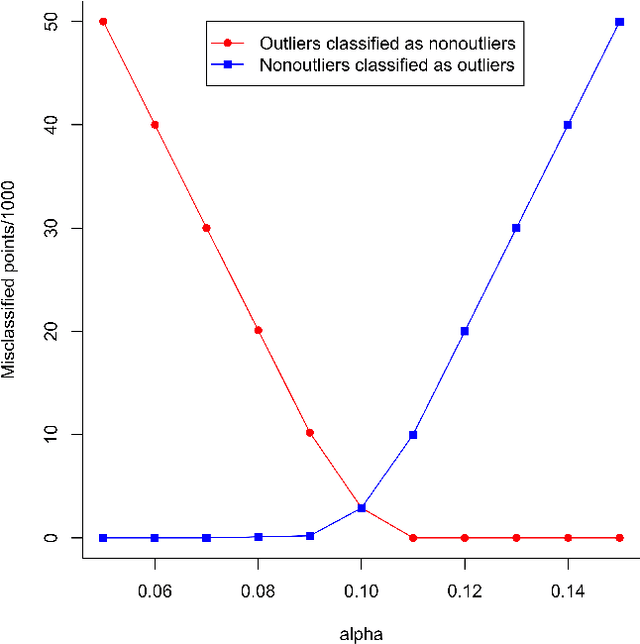
Mixtures of Gaussian distributions are a popular choice in model-based clustering. Outliers can affect parameters estimation and, as such, must be accounted for. Algorithms such as TCLUST discern the most likely outliers, but only when the proportion of outlying points is known \textit{a priori}. It is proved that, for a finite Gaussian mixture model, the log-likelihoods of the subset models are beta-distributed. An algorithm is then proposed that predicts the proportion of outliers by measuring the adherence of a set of subset log-likelihoods to a beta reference distribution. This algorithm removes the least likely points, which are deemed outliers, until model assumptions are met.