Using Subset Log-Likelihoods to Trim Outliers in Gaussian Mixture Models

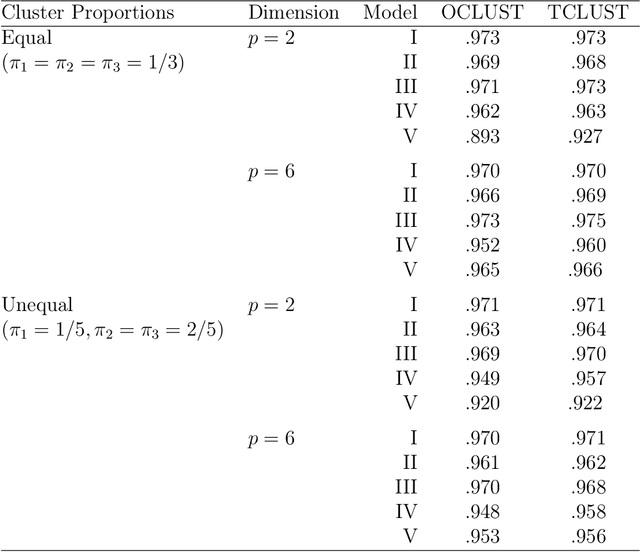
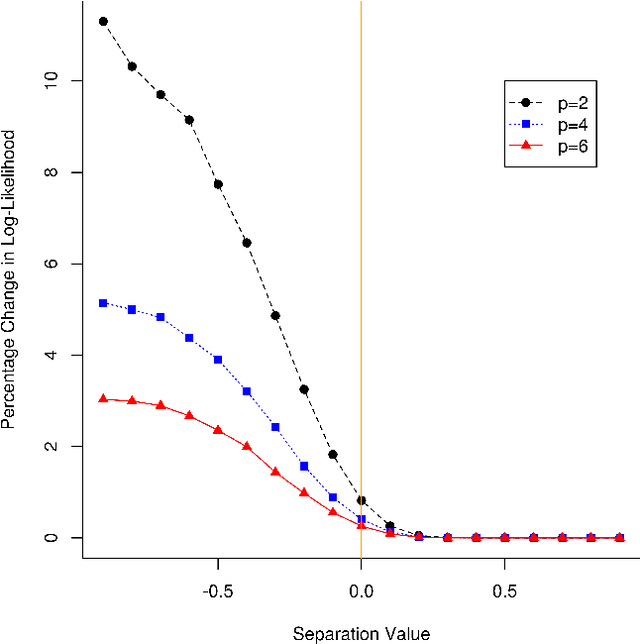
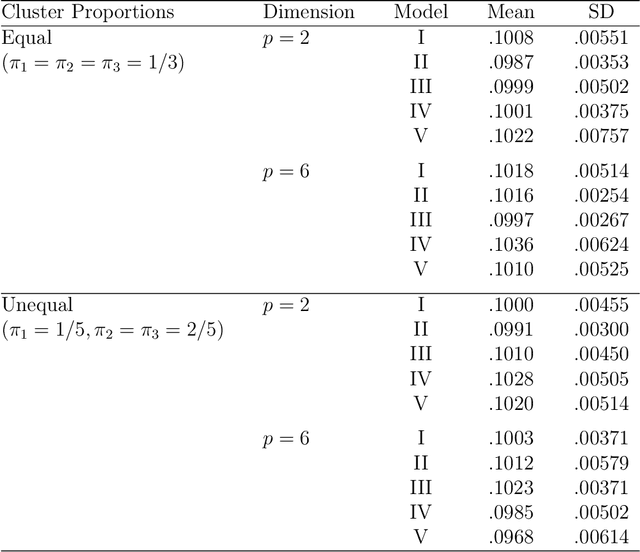
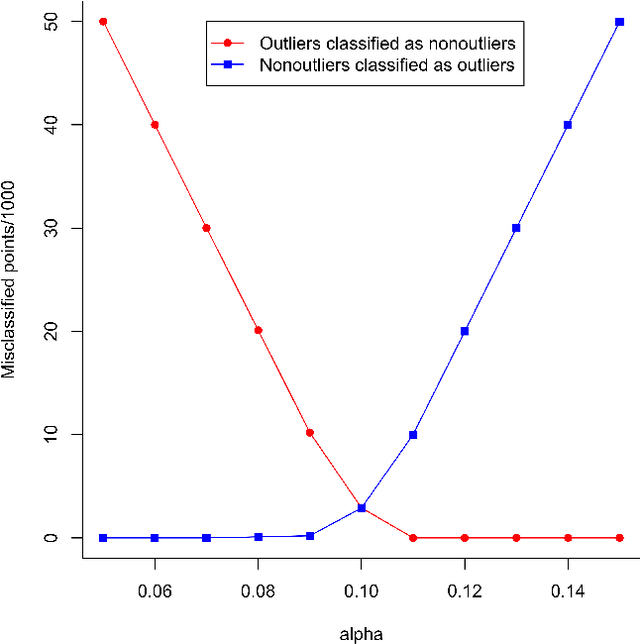
Mixtures of Gaussian distributions are a popular choice in model-based clustering. Outliers can affect parameters estimation and, as such, must be accounted for. Algorithms such as TCLUST discern the most likely outliers, but only when the proportion of outlying points is known \textit{a priori}. It is proved that, for a finite Gaussian mixture model, the log-likelihoods of the subset models are beta-distributed. An algorithm is then proposed that predicts the proportion of outliers by measuring the adherence of a set of subset log-likelihoods to a beta reference distribution. This algorithm removes the least likely points, which are deemed outliers, until model assumptions are met.