Finite Mixtures of Multivariate Poisson-Log Normal Factor Analyzers for Clustering Count Data

A mixture of multivariate Poisson-log normal factor analyzers is introduced by imposing constraints on the covariance matrix, which resulted in flexible models for clustering purposes. In particular, a class of eight parsimonious mixture models based on the mixtures of factor analyzers model are introduced. Variational Gaussian approximation is used for parameter estimation, and information criteria are used for model selection. The proposed models are explored in the context of clustering discrete data arising from RNA sequencing studies. Using real and simulated data, the models are shown to give favourable clustering performance. The GitHub R package for this work is available at https://github.com/anjalisilva/mixMPLNFA and is released under the open-source MIT license.

A Variational Approximations-DIC Rubric for Parameter Estimation and Mixture Model Selection Within a Family Setting

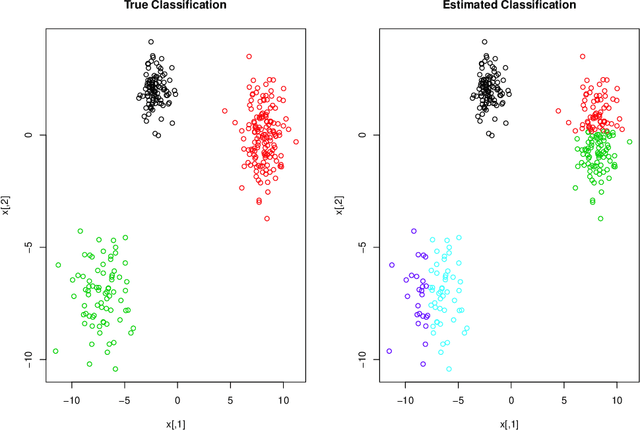
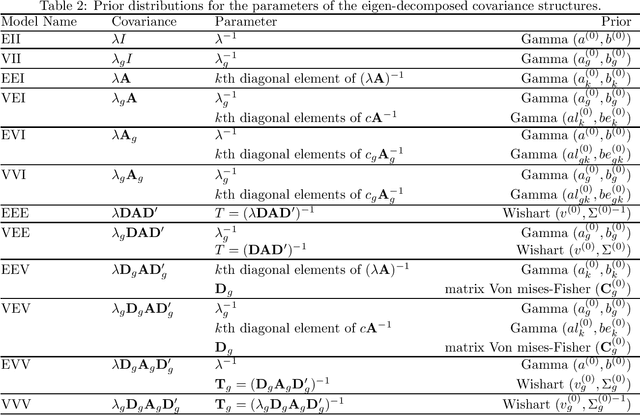
Mixture model-based clustering has become an increasingly popular data analysis technique since its introduction fifty years ago, and is now commonly utilized within the family setting. Families of mixture models arise when the component parameters, usually the component covariance matrices, are decomposed and a number of constraints are imposed. Within the family setting, we need to choose the member of the family, i.e., the appropriate covariance structure, in addition to the number of mixture components. To date, the Bayesian information criterion (BIC) has proved most effective for model selection, and the expectation-maximization (EM) algorithm is usually used for parameter estimation. To date, this EM-BIC rubric has monopolized the literature on families of mixture models. We deviate from this rubric, using variational Bayes approximations for parameter estimation and the deviance information criterion for model selection. The variational Bayes approach alleviates some of the computational complexities associated with the EM algorithm by constructing a tight lower bound on the complex marginal likelihood and maximizing this lower bound by minimizing the associated Kullback-Leibler divergence. We use this approach on the most famous family of Gaussian mixture models within the literature and real and simulated data are used to compare our approach to the EM-BIC rubric.

Variational Bayes Approximations for Clustering via Mixtures of Normal Inverse Gaussian Distributions

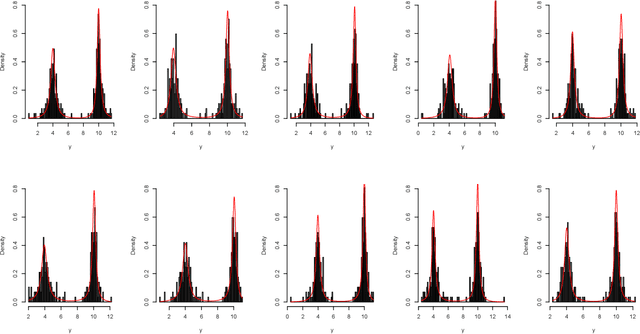
Parameter estimation for model-based clustering using a finite mixture of normal inverse Gaussian (NIG) distributions is achieved through variational Bayes approximations. Univariate NIG mixtures and multivariate NIG mixtures are considered. The use of variational Bayes approximations here is a substantial departure from the traditional EM approach and alleviates some of the associated computational complexities and uncertainties. Our variational algorithm is applied to simulated and real data. The paper concludes with discussion and suggestions for future work.

Constrained Optimization for a Subset of the Gaussian Parsimonious Clustering Models

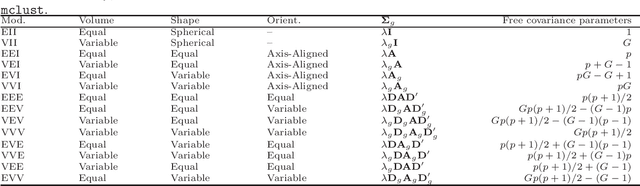
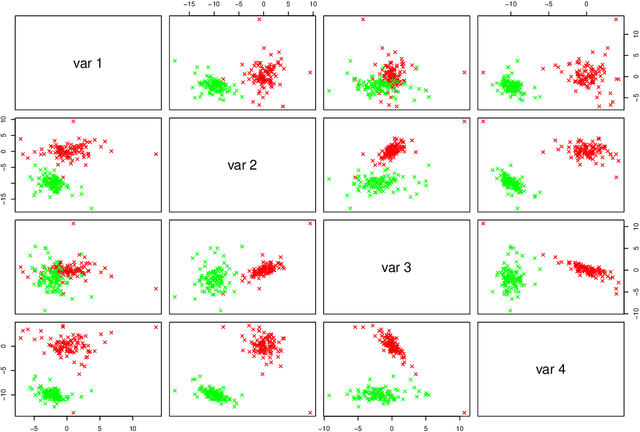
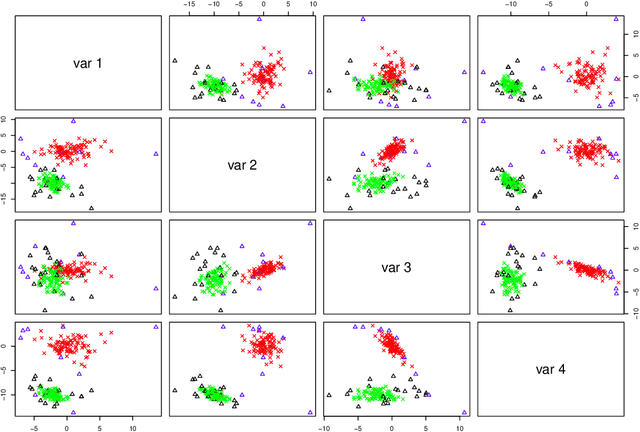
The expectation-maximization (EM) algorithm is an iterative method for finding maximum likelihood estimates when data are incomplete or are treated as being incomplete. The EM algorithm and its variants are commonly used for parameter estimation in applications of mixture models for clustering and classification. This despite the fact that even the Gaussian mixture model likelihood surface contains many local maxima and is singularity riddled. Previous work has focused on circumventing this problem by constraining the smallest eigenvalue of the component covariance matrices. In this paper, we consider constraining the smallest eigenvalue, the largest eigenvalue, and both the smallest and largest within the family setting. Specifically, a subset of the GPCM family is considered for model-based clustering, where we use a re-parameterized version of the famous eigenvalue decomposition of the component covariance matrices. Our approach is illustrated using various experiments with simulated and real data.