Constrained Optimization for a Subset of the Gaussian Parsimonious Clustering Models
Paper and Code
Jun 25, 2013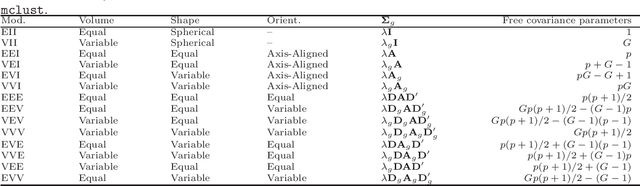
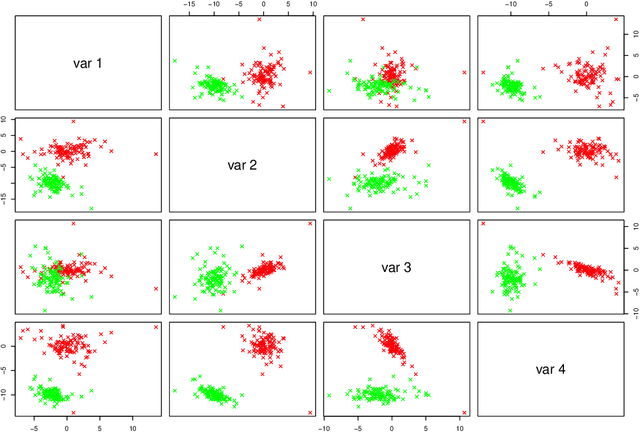

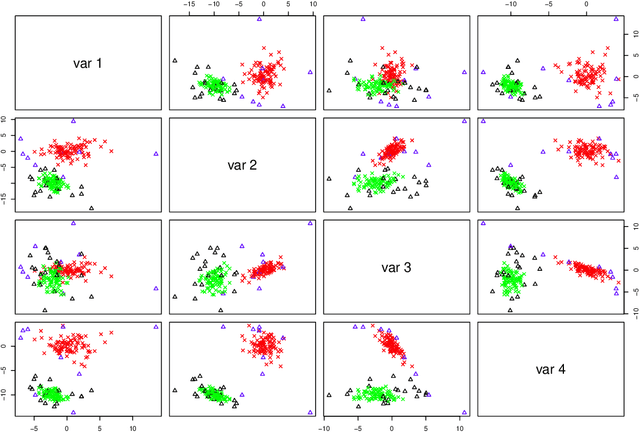
The expectation-maximization (EM) algorithm is an iterative method for finding maximum likelihood estimates when data are incomplete or are treated as being incomplete. The EM algorithm and its variants are commonly used for parameter estimation in applications of mixture models for clustering and classification. This despite the fact that even the Gaussian mixture model likelihood surface contains many local maxima and is singularity riddled. Previous work has focused on circumventing this problem by constraining the smallest eigenvalue of the component covariance matrices. In this paper, we consider constraining the smallest eigenvalue, the largest eigenvalue, and both the smallest and largest within the family setting. Specifically, a subset of the GPCM family is considered for model-based clustering, where we use a re-parameterized version of the famous eigenvalue decomposition of the component covariance matrices. Our approach is illustrated using various experiments with simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge