One Line To Rule Them All: Generating LO-Shot Soft-Label Prototypes

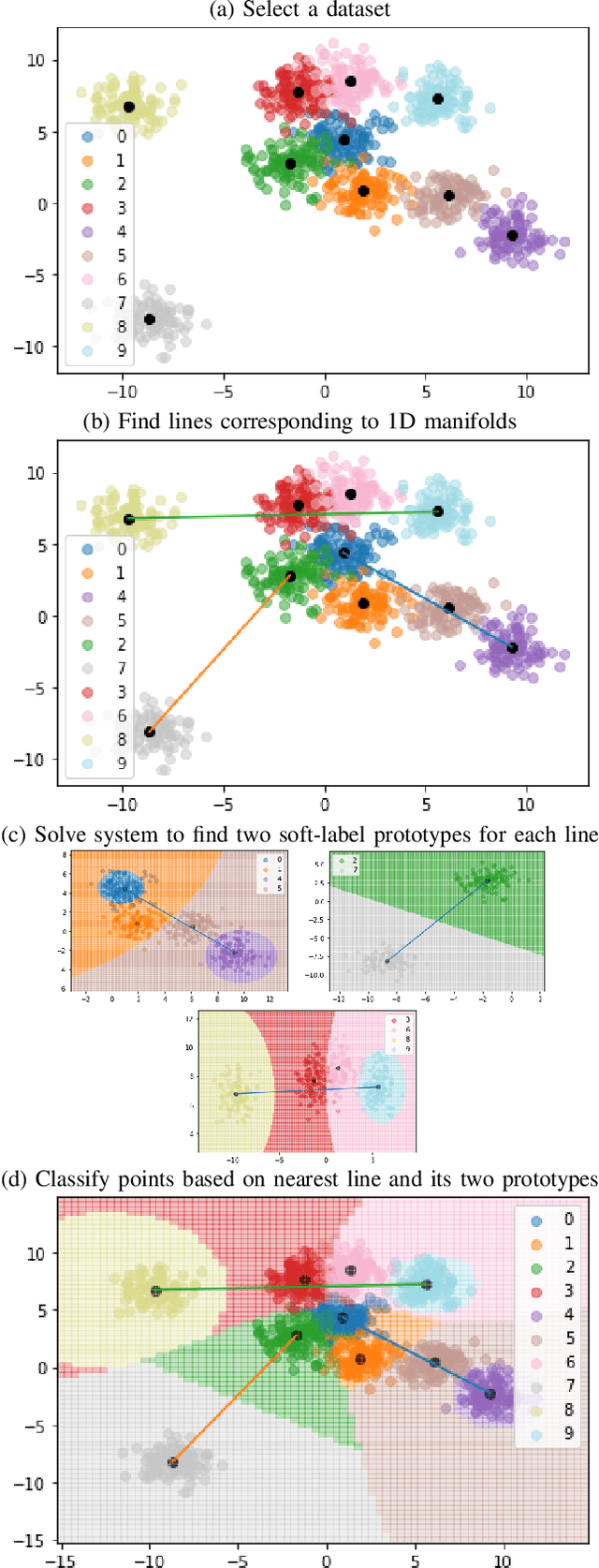
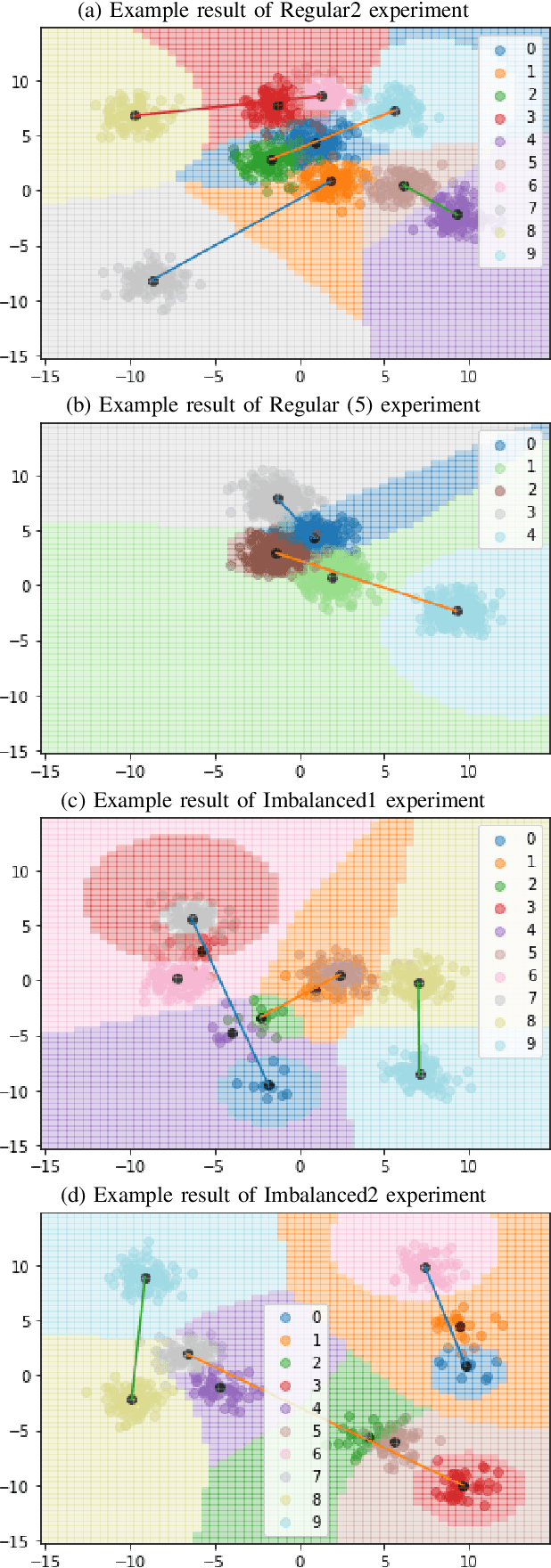
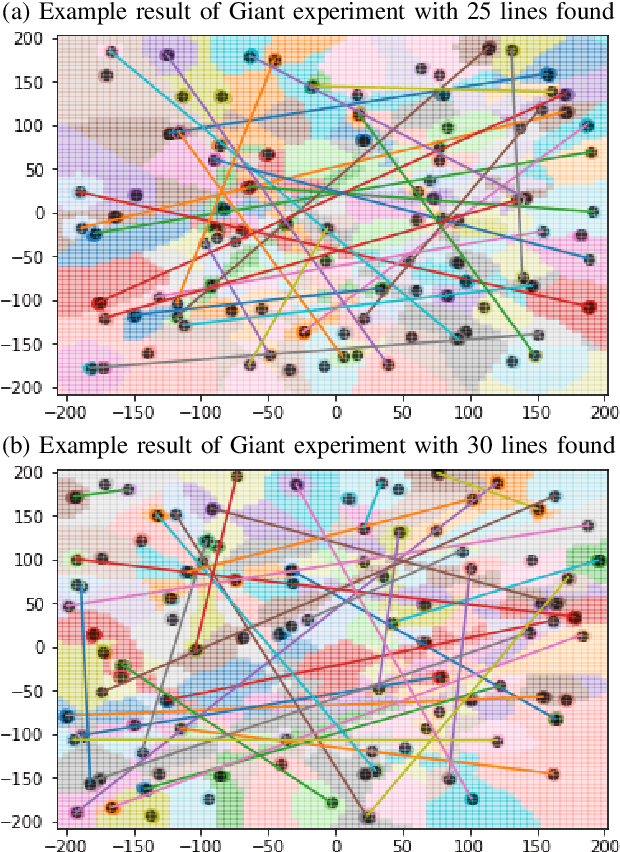
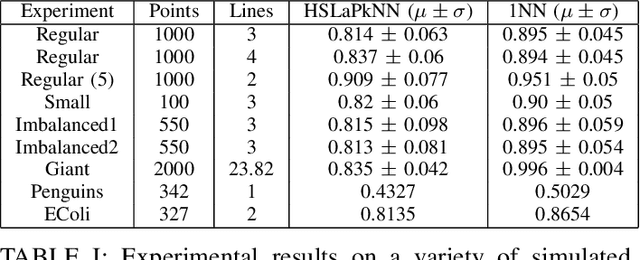
Increasingly large datasets are rapidly driving up the computational costs of machine learning. Prototype generation methods aim to create a small set of synthetic observations that accurately represent a training dataset but greatly reduce the computational cost of learning from it. Assigning soft labels to prototypes can allow increasingly small sets of prototypes to accurately represent the original training dataset. Although foundational work on `less than one'-shot learning has proven the theoretical plausibility of learning with fewer than one observation per class, developing practical algorithms for generating such prototypes remains an unexplored territory. We propose a novel, modular method for generating soft-label prototypical lines that still maintains representational accuracy even when there are fewer prototypes than the number of classes in the data. In addition, we propose the Hierarchical Soft-Label Prototype k-Nearest Neighbor classification algorithm based on these prototypical lines. We show that our method maintains high classification accuracy while greatly reducing the number of prototypes required to represent a dataset, even when working with severely imbalanced and difficult data. Our code is available at https://github.com/ilia10000/SLkNN.

Asymmetric Clusters and Outliers: Mixtures of Multivariate Contaminated Shifted Asymmetric Laplace Distributions

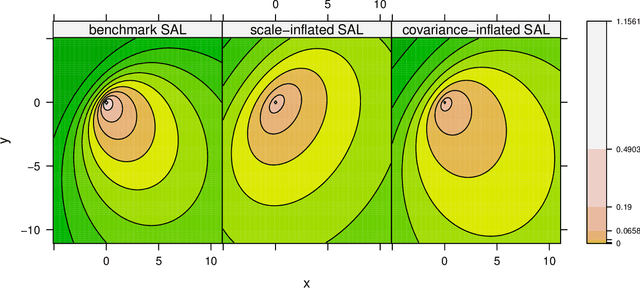
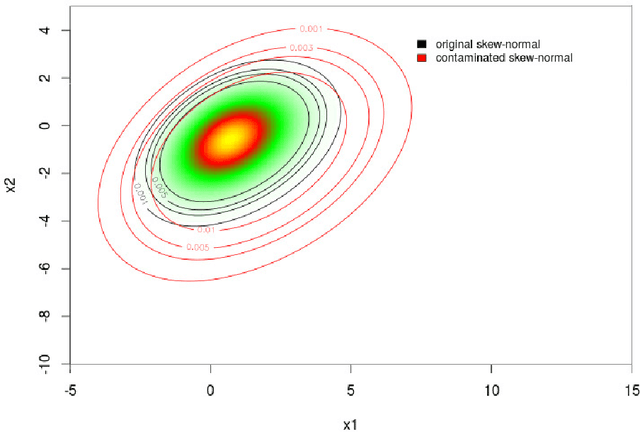
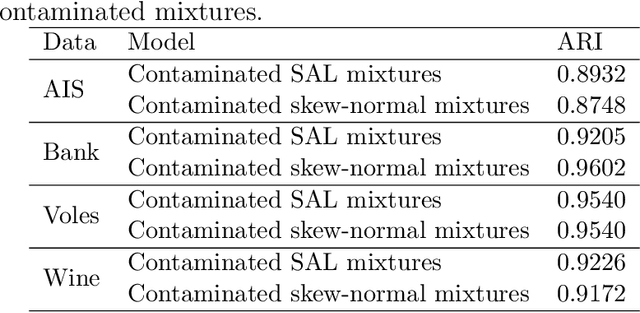
Mixtures of multivariate contaminated shifted asymmetric Laplace distributions are developed for handling asymmetric clusters in the presence of outliers (also referred to as bad points herein). In addition to the parameters of the related non-contaminated mixture, for each (asymmetric) cluster, our model has one parameter controlling the proportion of outliers and one specifying the degree of contamination. Crucially, these parameters do not have to be specified a priori, adding a flexibility to our approach that is absent from other approaches such as trimming. Moreover, each observation is given a posterior probability of belonging to a particular cluster, and of being an outlier or not; advantageously, this allows for the automatic detection of outliers. An expectation-conditional maximization algorithm is outlined for parameter estimation and various implementation issues are discussed. The behaviour of the proposed model is investigated, and compared with well-established finite mixtures, on artificial and real data.

Multivariate response and parsimony for Gaussian cluster-weighted models

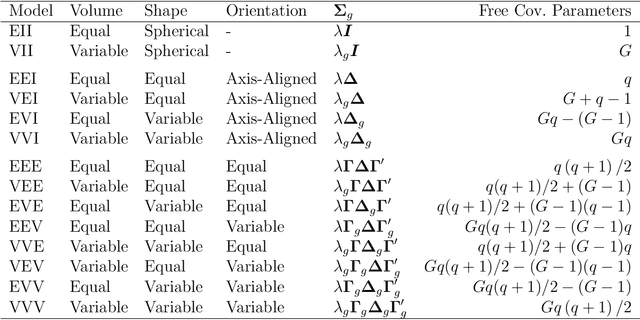
A family of parsimonious Gaussian cluster-weighted models is presented. This family concerns a multivariate extension to cluster-weighted modelling that can account for correlations between multivariate responses. Parsimony is attained by constraining parts of an eigen-decomposition imposed on the component covariance matrices. A sufficient condition for identifiability is provided and an expectation-maximization algorithm is presented for parameter estimation. Model performance is investigated on both synthetic and classical real data sets and compared with some popular approaches. Finally, accounting for linear dependencies in the presence of a linear regression structure is shown to offer better performance, vis-\`{a}-vis clustering, over existing methodologies.

A Mixture of Generalized Hyperbolic Factor Analyzers

Model-based clustering imposes a finite mixture modelling structure on data for clustering. Finite mixture models assume that the population is a convex combination of a finite number of densities, the distribution within each population is a basic assumption of each particular model. Among all distributions that have been tried, the generalized hyperbolic distribution has the advantage that is a generalization of several other methods, such as the Gaussian distribution, the skew t-distribution, etc. With specific parameters, it can represent either a symmetric or a skewed distribution. While its inherent flexibility is an advantage in many ways, it means the estimation of more parameters than its special and limiting cases. The aim of this work is to propose a mixture of generalized hyperbolic factor analyzers to introduce parsimony and extend the method to high dimensional data. This work can be seen as an extension of the mixture of factor analyzers model to generalized hyperbolic mixtures. The performance of our generalized hyperbolic factor analyzers is illustrated on real data, where it performs favourably compared to its Gaussian analogue.

Model Based Clustering of High-Dimensional Binary Data

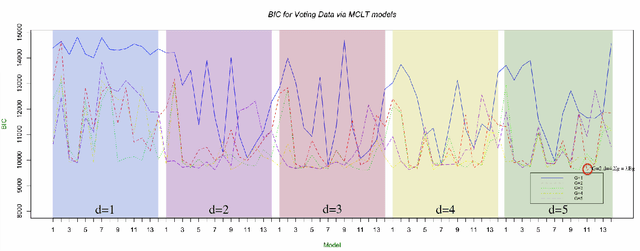
We propose a mixture of latent trait models with common slope parameters (MCLT) for model-based clustering of high-dimensional binary data, a data type for which few established methods exist. Recent work on clustering of binary data, based on a $d$-dimensional Gaussian latent variable, is extended by incorporating common factor analyzers. Accordingly, our approach facilitates a low-dimensional visual representation of the clusters. We extend the model further by the incorporation of random block effects. The dependencies in each block are taken into account through block-specific parameters that are considered to be random variables. A variational approximation to the likelihood is exploited to derive a fast algorithm for determining the model parameters. Our approach is demonstrated on real and simulated data.

Parsimonious Shifted Asymmetric Laplace Mixtures

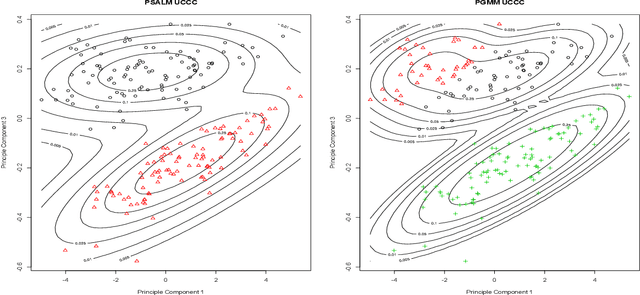
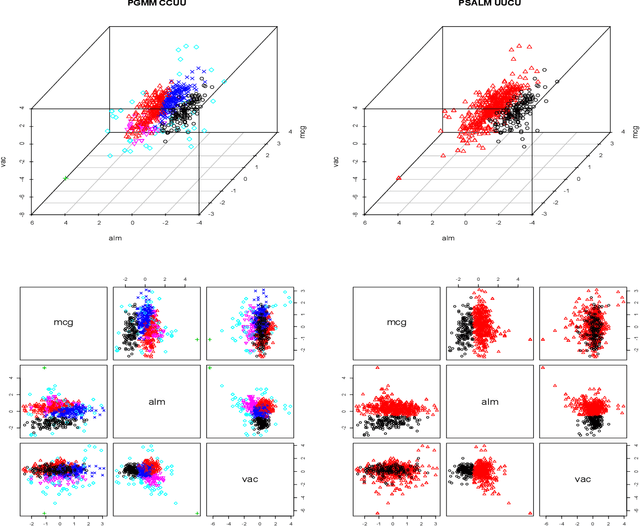
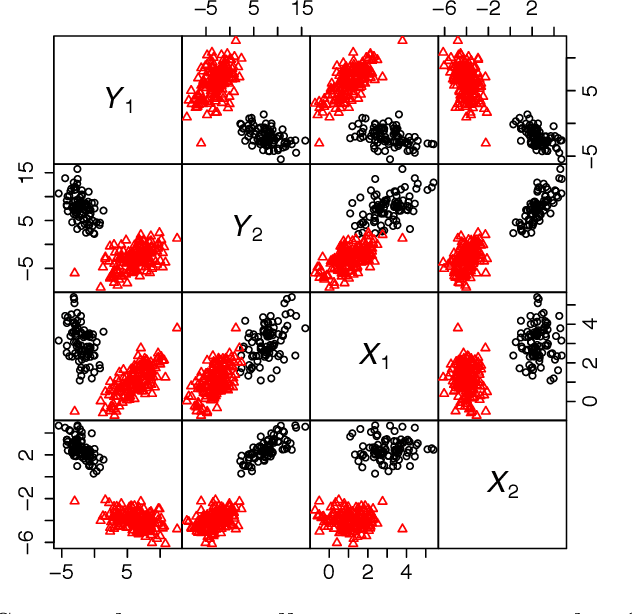
A family of parsimonious shifted asymmetric Laplace mixture models is introduced. We extend the mixture of factor analyzers model to the shifted asymmetric Laplace distribution. Imposing constraints on the constitute parts of the resulting decomposed component scale matrices leads to a family of parsimonious models. An explicit two-stage parameter estimation procedure is described, and the Bayesian information criterion and the integrated completed likelihood are compared for model selection. This novel family of models is applied to real data, where it is compared to its Gaussian analogue within clustering and classification paradigms.

Mixtures of Common Skew-t Factor Analyzers

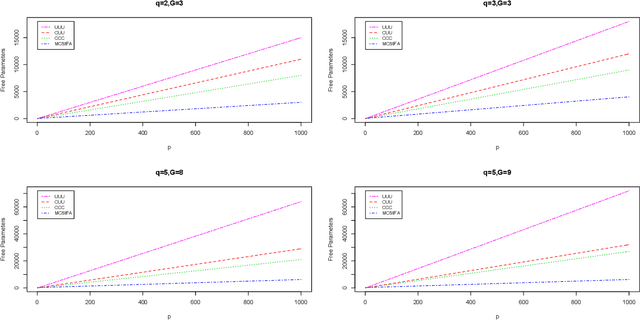
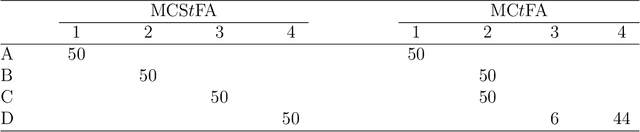
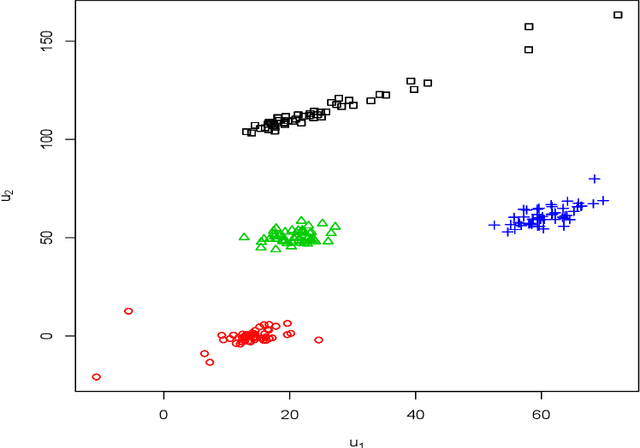
A mixture of common skew-t factor analyzers model is introduced for model-based clustering of high-dimensional data. By assuming common component factor loadings, this model allows clustering to be performed in the presence of a large number of mixture components or when the number of dimensions is too large to be well-modelled by the mixtures of factor analyzers model or a variant thereof. Furthermore, assuming that the component densities follow a skew-t distribution allows robust clustering of skewed data. The alternating expectation-conditional maximization algorithm is employed for parameter estimation. We demonstrate excellent clustering performance when our model is applied to real and simulated data.This paper marks the first time that skewed common factors have been used.

Constrained Optimization for a Subset of the Gaussian Parsimonious Clustering Models

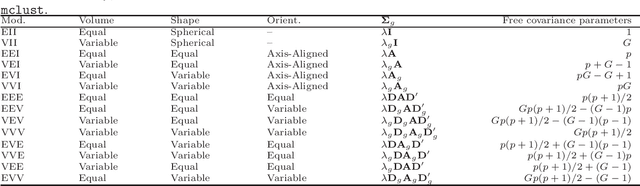
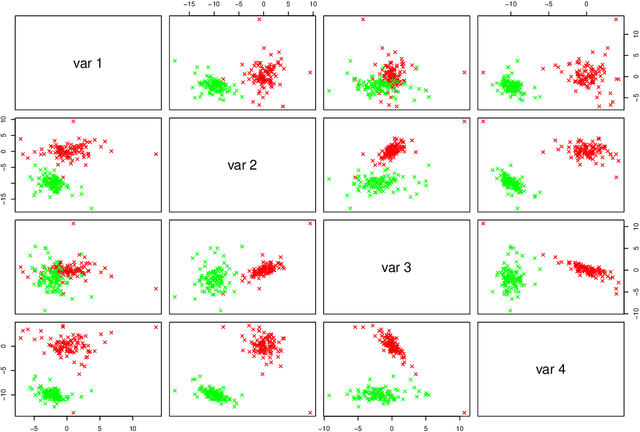
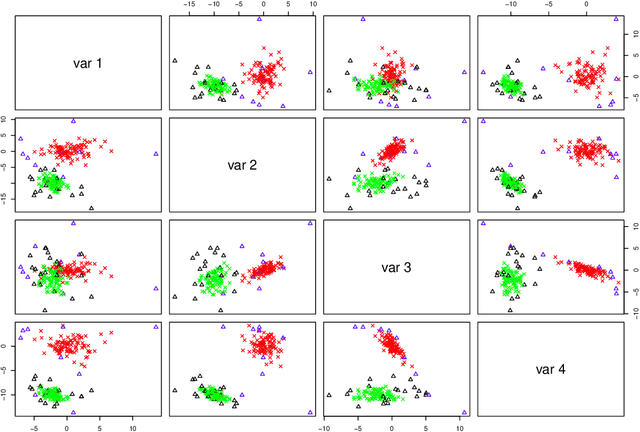
The expectation-maximization (EM) algorithm is an iterative method for finding maximum likelihood estimates when data are incomplete or are treated as being incomplete. The EM algorithm and its variants are commonly used for parameter estimation in applications of mixture models for clustering and classification. This despite the fact that even the Gaussian mixture model likelihood surface contains many local maxima and is singularity riddled. Previous work has focused on circumventing this problem by constraining the smallest eigenvalue of the component covariance matrices. In this paper, we consider constraining the smallest eigenvalue, the largest eigenvalue, and both the smallest and largest within the family setting. Specifically, a subset of the GPCM family is considered for model-based clustering, where we use a re-parameterized version of the famous eigenvalue decomposition of the component covariance matrices. Our approach is illustrated using various experiments with simulated and real data.

Mixtures of Shifted Asymmetric Laplace Distributions

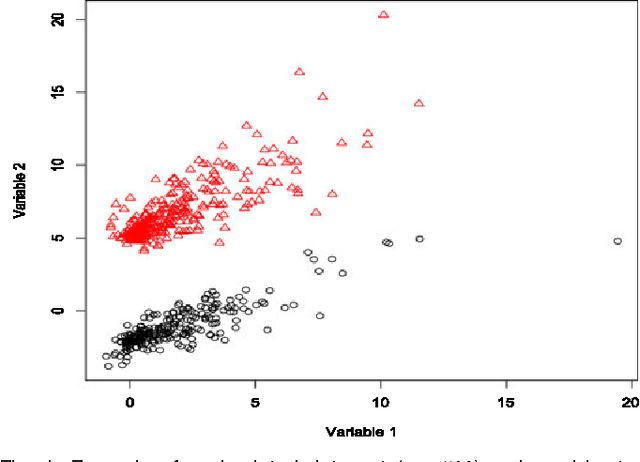
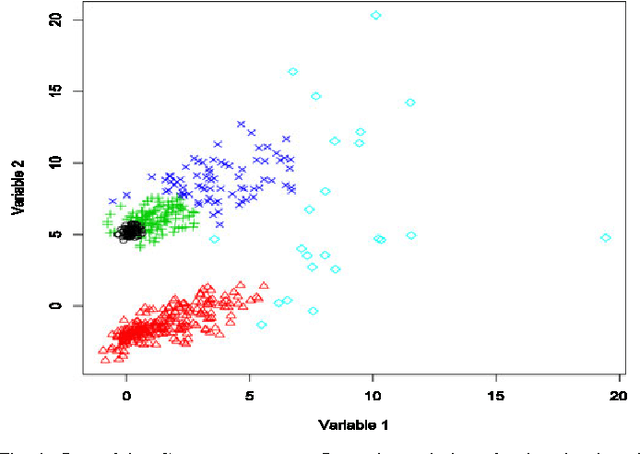
A mixture of shifted asymmetric Laplace distributions is introduced and used for clustering and classification. A variant of the EM algorithm is developed for parameter estimation by exploiting the relationship with the general inverse Gaussian distribution. This approach is mathematically elegant and relatively computationally straightforward. Our novel mixture modelling approach is demonstrated on both simulated and real data to illustrate clustering and classification applications. In these analyses, our mixture of shifted asymmetric Laplace distributions performs favourably when compared to the popular Gaussian approach. This work, which marks an important step in the non-Gaussian model-based clustering and classification direction, concludes with discussion as well as suggestions for future work.