Parsimonious Shifted Asymmetric Laplace Mixtures

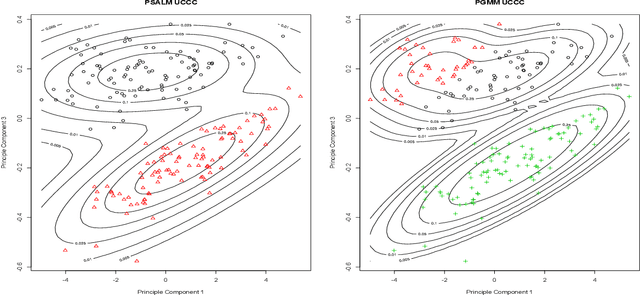
A family of parsimonious shifted asymmetric Laplace mixture models is introduced. We extend the mixture of factor analyzers model to the shifted asymmetric Laplace distribution. Imposing constraints on the constitute parts of the resulting decomposed component scale matrices leads to a family of parsimonious models. An explicit two-stage parameter estimation procedure is described, and the Bayesian information criterion and the integrated completed likelihood are compared for model selection. This novel family of models is applied to real data, where it is compared to its Gaussian analogue within clustering and classification paradigms.

Mixtures of Common Skew-t Factor Analyzers

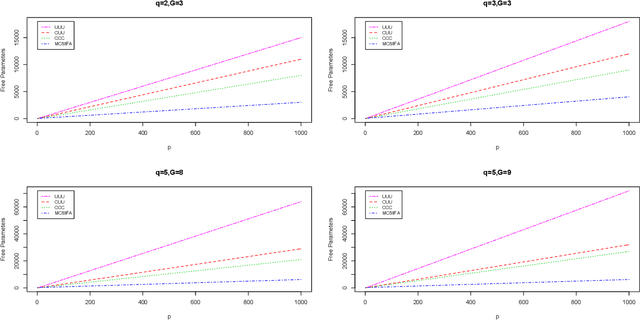
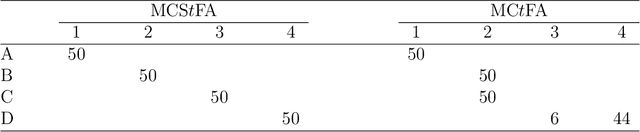
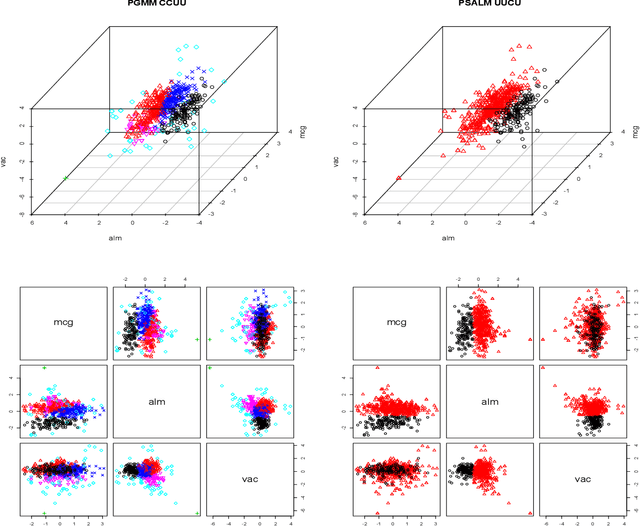
A mixture of common skew-t factor analyzers model is introduced for model-based clustering of high-dimensional data. By assuming common component factor loadings, this model allows clustering to be performed in the presence of a large number of mixture components or when the number of dimensions is too large to be well-modelled by the mixtures of factor analyzers model or a variant thereof. Furthermore, assuming that the component densities follow a skew-t distribution allows robust clustering of skewed data. The alternating expectation-conditional maximization algorithm is employed for parameter estimation. We demonstrate excellent clustering performance when our model is applied to real and simulated data.This paper marks the first time that skewed common factors have been used.