Parsimonious Shifted Asymmetric Laplace Mixtures

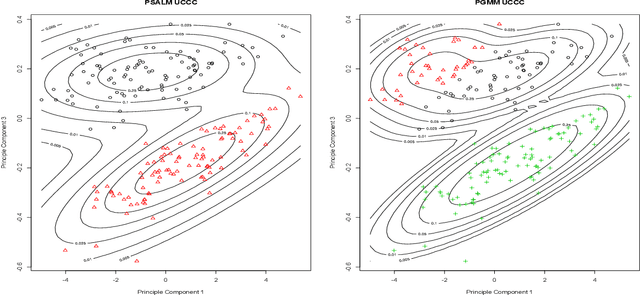
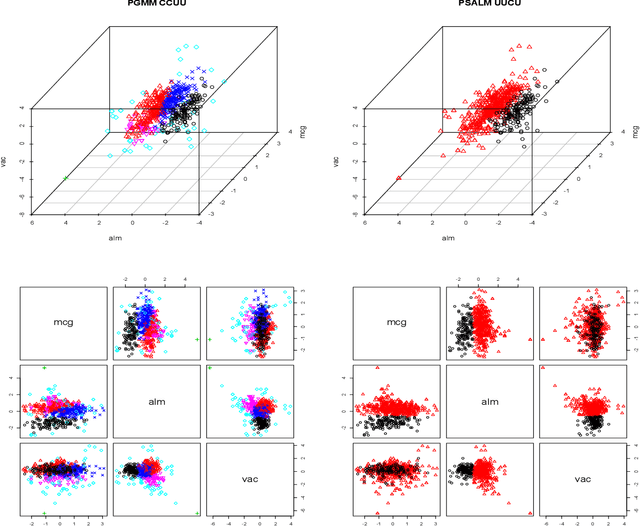
A family of parsimonious shifted asymmetric Laplace mixture models is introduced. We extend the mixture of factor analyzers model to the shifted asymmetric Laplace distribution. Imposing constraints on the constitute parts of the resulting decomposed component scale matrices leads to a family of parsimonious models. An explicit two-stage parameter estimation procedure is described, and the Bayesian information criterion and the integrated completed likelihood are compared for model selection. This novel family of models is applied to real data, where it is compared to its Gaussian analogue within clustering and classification paradigms.

Mixtures of Shifted Asymmetric Laplace Distributions

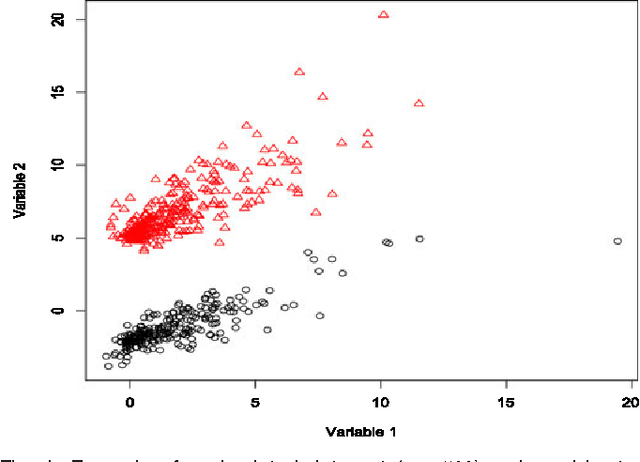
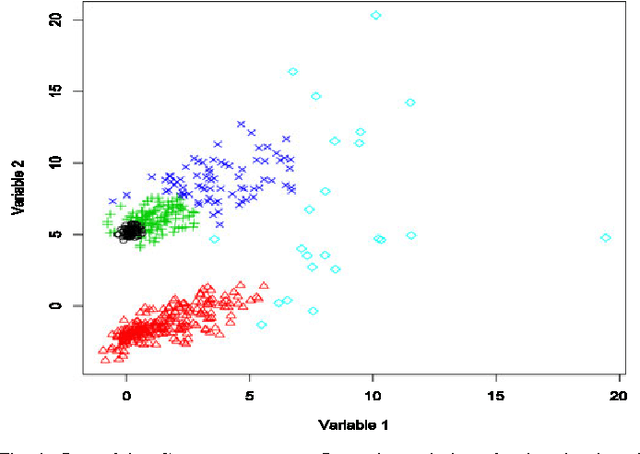
A mixture of shifted asymmetric Laplace distributions is introduced and used for clustering and classification. A variant of the EM algorithm is developed for parameter estimation by exploiting the relationship with the general inverse Gaussian distribution. This approach is mathematically elegant and relatively computationally straightforward. Our novel mixture modelling approach is demonstrated on both simulated and real data to illustrate clustering and classification applications. In these analyses, our mixture of shifted asymmetric Laplace distributions performs favourably when compared to the popular Gaussian approach. This work, which marks an important step in the non-Gaussian model-based clustering and classification direction, concludes with discussion as well as suggestions for future work.