Salvatore Ingrassia
Multivariate response and parsimony for Gaussian cluster-weighted models
Feb 26, 2016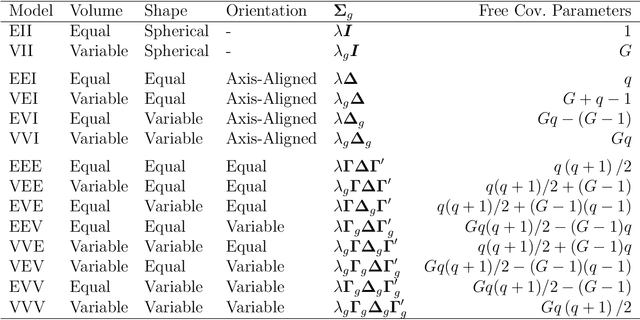
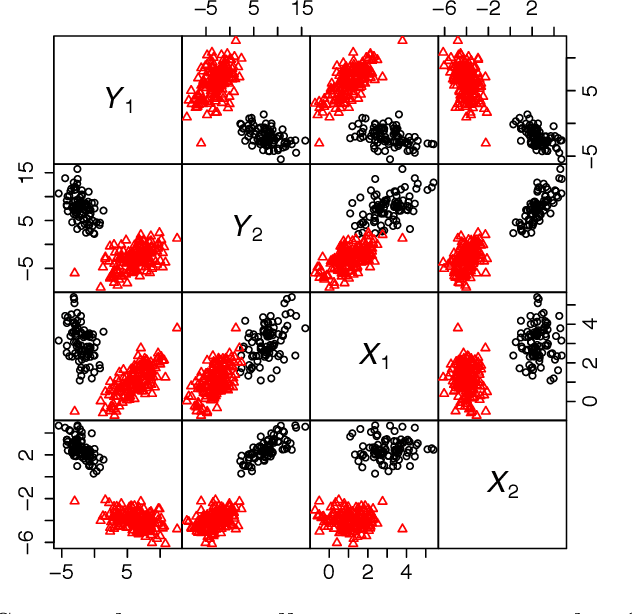


Abstract:A family of parsimonious Gaussian cluster-weighted models is presented. This family concerns a multivariate extension to cluster-weighted modelling that can account for correlations between multivariate responses. Parsimony is attained by constraining parts of an eigen-decomposition imposed on the component covariance matrices. A sufficient condition for identifiability is provided and an expectation-maximization algorithm is presented for parameter estimation. Model performance is investigated on both synthetic and classical real data sets and compared with some popular approaches. Finally, accounting for linear dependencies in the presence of a linear regression structure is shown to offer better performance, vis-\`{a}-vis clustering, over existing methodologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge