Asymmetric Clusters and Outliers: Mixtures of Multivariate Contaminated Shifted Asymmetric Laplace Distributions

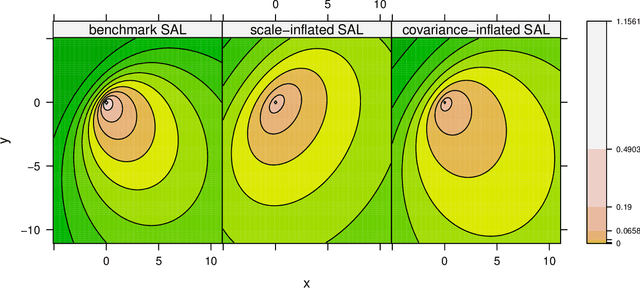
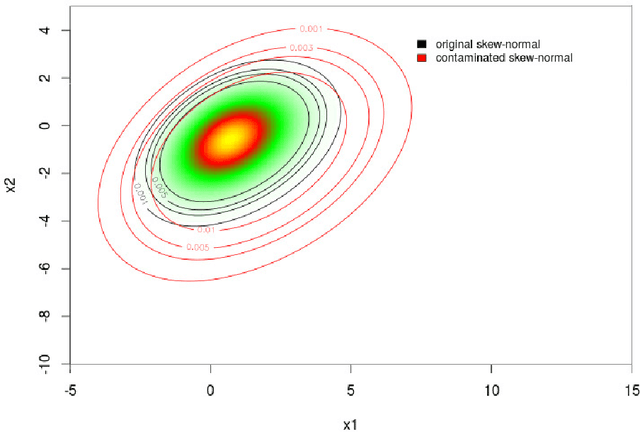
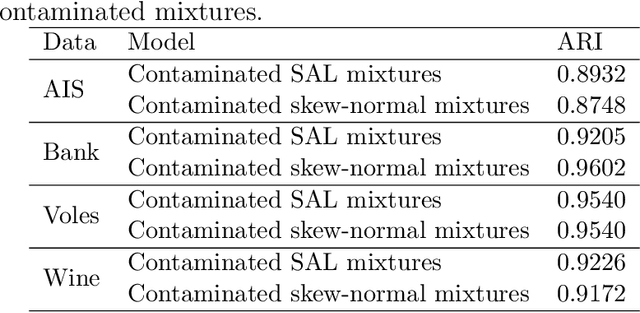
Mixtures of multivariate contaminated shifted asymmetric Laplace distributions are developed for handling asymmetric clusters in the presence of outliers (also referred to as bad points herein). In addition to the parameters of the related non-contaminated mixture, for each (asymmetric) cluster, our model has one parameter controlling the proportion of outliers and one specifying the degree of contamination. Crucially, these parameters do not have to be specified a priori, adding a flexibility to our approach that is absent from other approaches such as trimming. Moreover, each observation is given a posterior probability of belonging to a particular cluster, and of being an outlier or not; advantageously, this allows for the automatic detection of outliers. An expectation-conditional maximization algorithm is outlined for parameter estimation and various implementation issues are discussed. The behaviour of the proposed model is investigated, and compared with well-established finite mixtures, on artificial and real data.

Multivariate response and parsimony for Gaussian cluster-weighted models

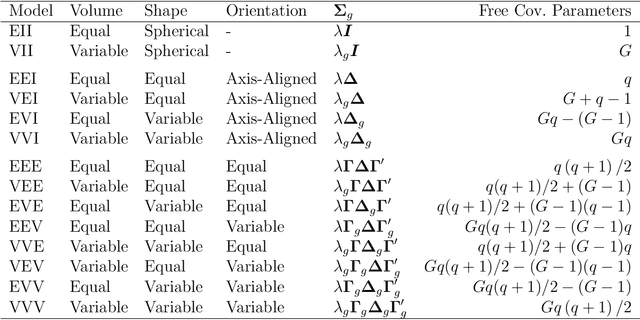
A family of parsimonious Gaussian cluster-weighted models is presented. This family concerns a multivariate extension to cluster-weighted modelling that can account for correlations between multivariate responses. Parsimony is attained by constraining parts of an eigen-decomposition imposed on the component covariance matrices. A sufficient condition for identifiability is provided and an expectation-maximization algorithm is presented for parameter estimation. Model performance is investigated on both synthetic and classical real data sets and compared with some popular approaches. Finally, accounting for linear dependencies in the presence of a linear regression structure is shown to offer better performance, vis-\`{a}-vis clustering, over existing methodologies.