Asymmetric Clusters and Outliers: Mixtures of Multivariate Contaminated Shifted Asymmetric Laplace Distributions

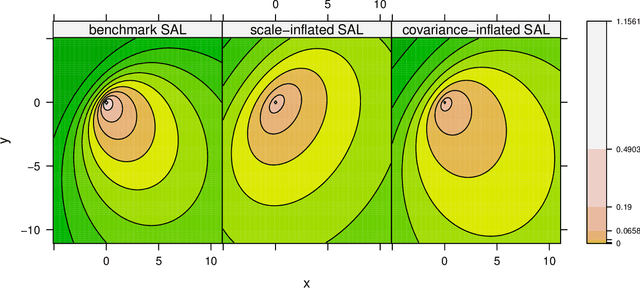
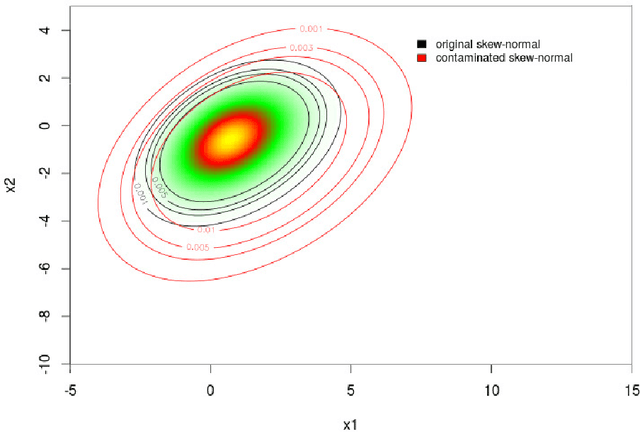
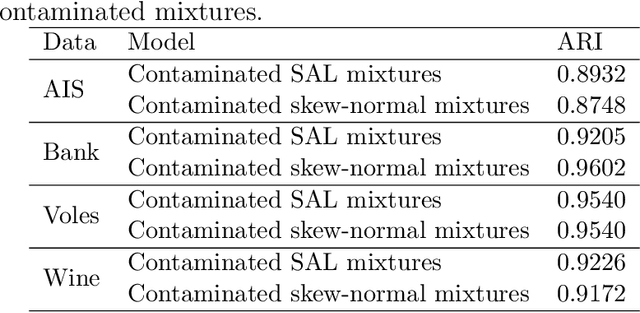
Mixtures of multivariate contaminated shifted asymmetric Laplace distributions are developed for handling asymmetric clusters in the presence of outliers (also referred to as bad points herein). In addition to the parameters of the related non-contaminated mixture, for each (asymmetric) cluster, our model has one parameter controlling the proportion of outliers and one specifying the degree of contamination. Crucially, these parameters do not have to be specified a priori, adding a flexibility to our approach that is absent from other approaches such as trimming. Moreover, each observation is given a posterior probability of belonging to a particular cluster, and of being an outlier or not; advantageously, this allows for the automatic detection of outliers. An expectation-conditional maximization algorithm is outlined for parameter estimation and various implementation issues are discussed. The behaviour of the proposed model is investigated, and compared with well-established finite mixtures, on artificial and real data.

Clustering, Classification, Discriminant Analysis, and Dimension Reduction via Generalized Hyperbolic Mixtures

A method for dimension reduction with clustering, classification, or discriminant analysis is introduced. This mixture model-based approach is based on fitting generalized hyperbolic mixtures on a reduced subspace within the paradigm of model-based clustering, classification, or discriminant analysis. A reduced subspace of the data is derived by considering the extent to which group means and group covariances vary. The members of the subspace arise through linear combinations of the original data, and are ordered by importance via the associated eigenvalues. The observations can be projected onto the subspace, resulting in a set of variables that captures most of the clustering information available. The use of generalized hyperbolic mixtures gives a robust framework capable of dealing with skewed clusters. Although dimension reduction is increasingly in demand across many application areas, the authors are most familiar with biological applications and so two of the five real data examples are within that sphere. Simulated data are also used for illustration. The approach introduced herein can be considered the most general such approach available, and so we compare results to three special and limiting cases. Comparisons with several well established techniques illustrate its promising performance.