A Variational Approximations-DIC Rubric for Parameter Estimation and Mixture Model Selection Within a Family Setting

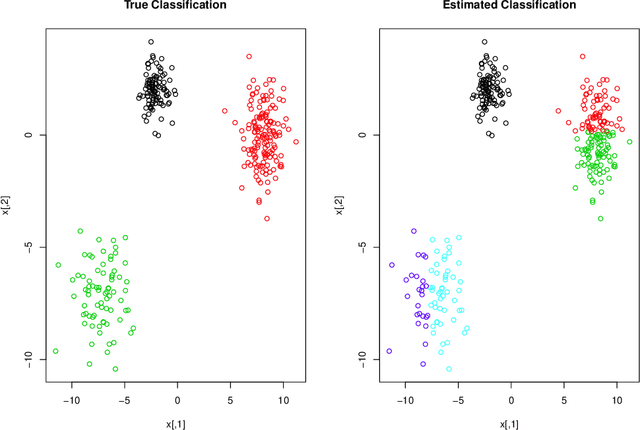
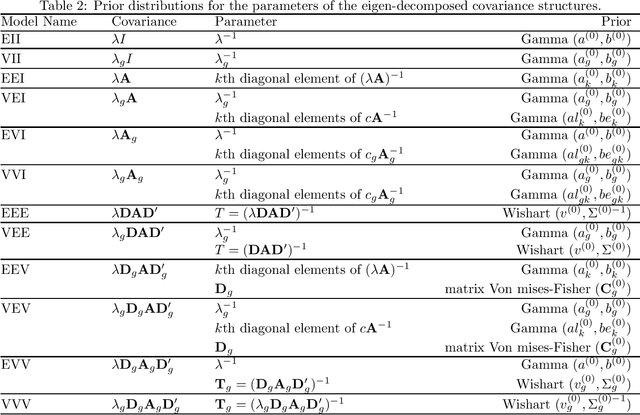
Mixture model-based clustering has become an increasingly popular data analysis technique since its introduction fifty years ago, and is now commonly utilized within the family setting. Families of mixture models arise when the component parameters, usually the component covariance matrices, are decomposed and a number of constraints are imposed. Within the family setting, we need to choose the member of the family, i.e., the appropriate covariance structure, in addition to the number of mixture components. To date, the Bayesian information criterion (BIC) has proved most effective for model selection, and the expectation-maximization (EM) algorithm is usually used for parameter estimation. To date, this EM-BIC rubric has monopolized the literature on families of mixture models. We deviate from this rubric, using variational Bayes approximations for parameter estimation and the deviance information criterion for model selection. The variational Bayes approach alleviates some of the computational complexities associated with the EM algorithm by constructing a tight lower bound on the complex marginal likelihood and maximizing this lower bound by minimizing the associated Kullback-Leibler divergence. We use this approach on the most famous family of Gaussian mixture models within the literature and real and simulated data are used to compare our approach to the EM-BIC rubric.