Kernel-Based Optimal Control: An Infinitesimal Generator Approach

This paper presents a novel approach for optimal control of nonlinear stochastic systems using infinitesimal generator learning within infinite-dimensional reproducing kernel Hilbert spaces. Our learning framework leverages data samples of system dynamics and stage cost functions, with only control penalties and constraints provided. The proposed method directly learns the diffusion operator of a controlled Fokker-Planck-Kolmogorov equation in an infinite-dimensional hypothesis space. This operator models the continuous-time evolution of the probability measure of the control system's state. We demonstrate that this approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions, enabling a data-driven solution to the optimal control problem. Furthermore, our statistical learning framework includes nonparametric estimators for uncontrolled forward infinitesimal generators as a special case. Numerical experiments, ranging from synthetic differential equations to simulated robotic systems, showcase the advantages of our approach compared to both modern data-driven and classical nonlinear programming methods for optimal control.

Real-Time-Feasible Collision-Free Motion Planning For Ellipsoidal Objects

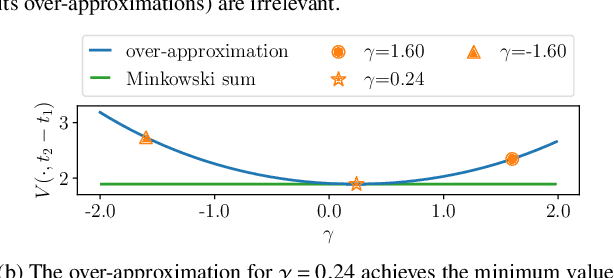
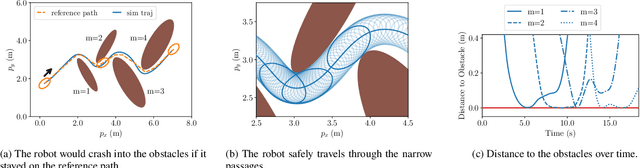
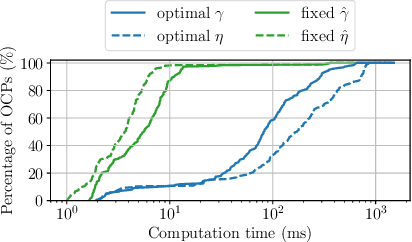
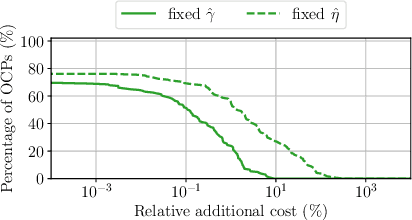
Online planning of collision-free trajectories is a fundamental task for robotics and self-driving car applications. This paper revisits collision avoidance between ellipsoidal objects using differentiable constraints. Two ellipsoids do not overlap if and only if the endpoint of the vector between the center points of the ellipsoids does not lie in the interior of the Minkowski sum of the ellipsoids. This condition is formulated using a parametric over-approximation of the Minkowski sum, which can be made tight in any given direction. The resulting collision avoidance constraint is included in an optimal control problem (OCP) and evaluated in comparison to the separating-hyperplane approach. Not only do we observe that the Minkowski-sum formulation is computationally more efficient in our experiments, but also that using pre-determined over-approximation parameters based on warm-start trajectories leads to a very limited increase in suboptimality. This gives rise to a novel real-time scheme for collision-free motion planning with model predictive control (MPC). Both the real-time feasibility and the effectiveness of the constraint formulation are demonstrated in challenging real-world experiments.

Data-Driven Optimal Feedback Laws via Kernel Mean Embeddings

This paper proposes a fully data-driven approach for optimal control of nonlinear control-affine systems represented by a stochastic diffusion. The focus is on the scenario where both the nonlinear dynamics and stage cost functions are unknown, while only control penalty function and constraints are provided. Leveraging the theory of reproducing kernel Hilbert spaces, we introduce novel kernel mean embeddings (KMEs) to identify the Markov transition operators associated with controlled diffusion processes. The KME learning approach seamlessly integrates with modern convex operator-theoretic Hamilton-Jacobi-Bellman recursions. Thus, unlike traditional dynamic programming methods, our approach exploits the ``kernel trick'' to break the curse of dimensionality. We demonstrate the effectiveness of our method through numerical examples, highlighting its ability to solve a large class of nonlinear optimal control problems.