Semi-Infinite Programming for Collision-Avoidance in Optimal and Model Predictive Control

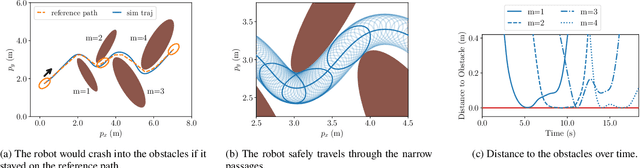
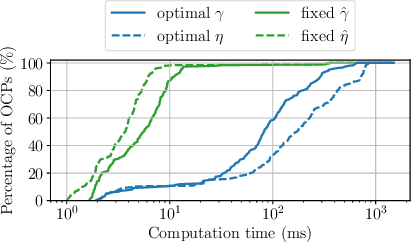
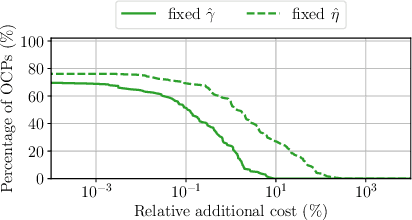
This paper presents a novel approach for collision avoidance in optimal and model predictive control, in which the environment is represented by a large number of points and the robot as a union of padded polygons. The conditions that none of the points shall collide with the robot can be written in terms of an infinite number of constraints per obstacle point. We show that the resulting semi-infinite programming (SIP) optimal control problem (OCP) can be efficiently tackled through a combination of two methods: local reduction and an external active-set method. Specifically, this involves iteratively identifying the closest point obstacles, determining the lower-level distance minimizer among all feasible robot shape parameters, and solving the upper-level finitely-constrained subproblems. In addition, this paper addresses robust collision avoidance in the presence of ellipsoidal state uncertainties. Enforcing constraint satisfaction over all possible uncertainty realizations extends the dimension of constraint infiniteness. The infinitely many constraints arising from translational uncertainty are handled by local reduction together with the robot shape parameterization, while rotational uncertainty is addressed via a backoff reformulation. A controller implemented based on the proposed method is demonstrated on a real-world robot running at 20Hz, enabling fast and collision-free navigation in tight spaces. An application to 3D collision avoidance is also demonstrated in simulation.

Synthesis of Model Predictive Control and Reinforcement Learning: Survey and Classification

The fields of MPC and RL consider two successful control techniques for Markov decision processes. Both approaches are derived from similar fundamental principles, and both are widely used in practical applications, including robotics, process control, energy systems, and autonomous driving. Despite their similarities, MPC and RL follow distinct paradigms that emerged from diverse communities and different requirements. Various technical discrepancies, particularly the role of an environment model as part of the algorithm, lead to methodologies with nearly complementary advantages. Due to their orthogonal benefits, research interest in combination methods has recently increased significantly, leading to a large and growing set of complex ideas leveraging MPC and RL. This work illuminates the differences, similarities, and fundamentals that allow for different combination algorithms and categorizes existing work accordingly. Particularly, we focus on the versatile actor-critic RL approach as a basis for our categorization and examine how the online optimization approach of MPC can be used to improve the overall closed-loop performance of a policy.

Real-Time-Feasible Collision-Free Motion Planning For Ellipsoidal Objects

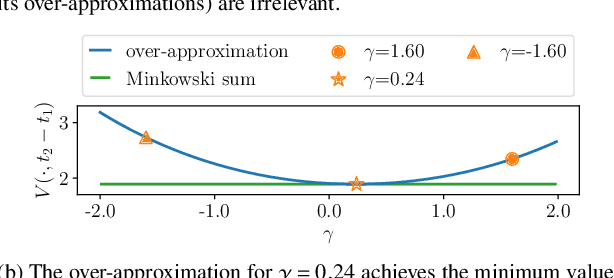
Online planning of collision-free trajectories is a fundamental task for robotics and self-driving car applications. This paper revisits collision avoidance between ellipsoidal objects using differentiable constraints. Two ellipsoids do not overlap if and only if the endpoint of the vector between the center points of the ellipsoids does not lie in the interior of the Minkowski sum of the ellipsoids. This condition is formulated using a parametric over-approximation of the Minkowski sum, which can be made tight in any given direction. The resulting collision avoidance constraint is included in an optimal control problem (OCP) and evaluated in comparison to the separating-hyperplane approach. Not only do we observe that the Minkowski-sum formulation is computationally more efficient in our experiments, but also that using pre-determined over-approximation parameters based on warm-start trajectories leads to a very limited increase in suboptimality. This gives rise to a novel real-time scheme for collision-free motion planning with model predictive control (MPC). Both the real-time feasibility and the effectiveness of the constraint formulation are demonstrated in challenging real-world experiments.

Stochastic Model Predictive Control with Optimal Linear Feedback for Mobile Robots in Dynamic Environments

Robot navigation around humans can be a challenging problem since human movements are hard to predict. Stochastic model predictive control (MPC) can account for such uncertainties and approximately bound the probability of a collision to take place. In this paper, to counteract the rapidly growing human motion uncertainty over time, we incorporate state feedback in the stochastic MPC. This allows the robot to more closely track reference trajectories. To this end the feedback policy is left as a degree of freedom in the optimal control problem. The stochastic MPC with feedback is validated in simulation experiments and is compared against nominal MPC and stochastic MPC without feedback. The added computation time can be limited by reducing the number of additional variables for the feedback law with a small compromise in control performance.