Katrin Baumgärtner
Differentiable Nonlinear Model Predictive Control
May 02, 2025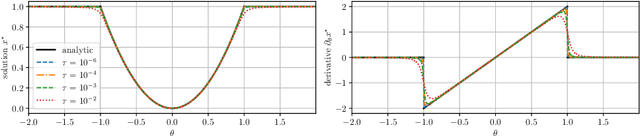

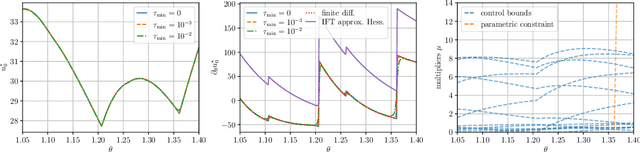

Abstract:The efficient computation of parametric solution sensitivities is a key challenge in the integration of learning-enhanced methods with nonlinear model predictive control (MPC), as their availability is crucial for many learning algorithms. While approaches presented in the machine learning community are limited to convex or unconstrained formulations, this paper discusses the computation of solution sensitivities of general nonlinear programs (NLPs) using the implicit function theorem (IFT) and smoothed optimality conditions treated in interior-point methods (IPM). We detail sensitivity computation within a sequential quadratic programming (SQP) method which employs an IPM for the quadratic subproblems. The publication is accompanied by an efficient open-source implementation within the framework, providing both forward and adjoint sensitivities for general optimal control problems, achieving speedups exceeding 3x over the state-of-the-art solver mpc.pytorch.
Synthesis of Model Predictive Control and Reinforcement Learning: Survey and Classification
Feb 04, 2025



Abstract:The fields of MPC and RL consider two successful control techniques for Markov decision processes. Both approaches are derived from similar fundamental principles, and both are widely used in practical applications, including robotics, process control, energy systems, and autonomous driving. Despite their similarities, MPC and RL follow distinct paradigms that emerged from diverse communities and different requirements. Various technical discrepancies, particularly the role of an environment model as part of the algorithm, lead to methodologies with nearly complementary advantages. Due to their orthogonal benefits, research interest in combination methods has recently increased significantly, leading to a large and growing set of complex ideas leveraging MPC and RL. This work illuminates the differences, similarities, and fundamentals that allow for different combination algorithms and categorizes existing work accordingly. Particularly, we focus on the versatile actor-critic RL approach as a basis for our categorization and examine how the online optimization approach of MPC can be used to improve the overall closed-loop performance of a policy.
AC4MPC: Actor-Critic Reinforcement Learning for Nonlinear Model Predictive Control
Jun 06, 2024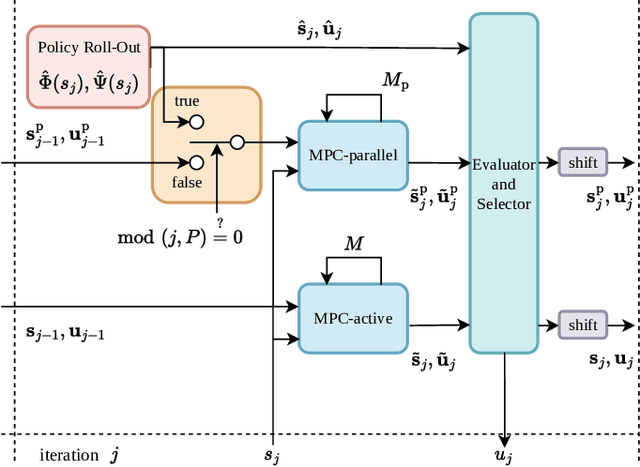
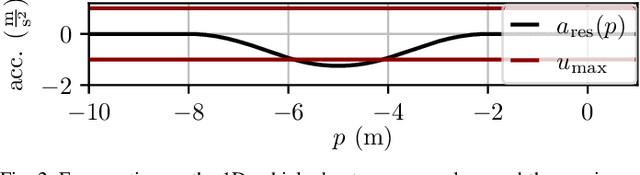
Abstract:\Ac{MPC} and \ac{RL} are two powerful control strategies with, arguably, complementary advantages. In this work, we show how actor-critic \ac{RL} techniques can be leveraged to improve the performance of \ac{MPC}. The \ac{RL} critic is used as an approximation of the optimal value function, and an actor roll-out provides an initial guess for primal variables of the \ac{MPC}. A parallel control architecture is proposed where each \ac{MPC} instance is solved twice for different initial guesses. Besides the actor roll-out initialization, a shifted initialization from the previous solution is used. Thereafter, the actor and the critic are again used to approximately evaluate the infinite horizon cost of these trajectories. The control actions from the lowest-cost trajectory are applied to the system at each time step. We establish that the proposed algorithm is guaranteed to outperform the original \ac{RL} policy plus an error term that depends on the accuracy of the critic and decays with the horizon length of the \ac{MPC} formulation. Moreover, we do not require globally optimal solutions for these guarantees to hold. The approach is demonstrated on an illustrative toy example and an \ac{AD} overtaking scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge