PA-MPPI: Perception-Aware Model Predictive Path Integral Control for Quadrotor Navigation in Unknown Environments

Quadrotor navigation in unknown environments is critical for practical missions such as search-and-rescue. Solving it requires addressing three key challenges: the non-convexity of free space due to obstacles, quadrotor-specific dynamics and objectives, and the need for exploration of unknown regions to find a path to the goal. Recently, the Model Predictive Path Integral (MPPI) method has emerged as a promising solution that solves the first two challenges. By leveraging sampling-based optimization, it can effectively handle non-convex free space while directly optimizing over the full quadrotor dynamics, enabling the inclusion of quadrotor-specific costs such as energy consumption. However, its performance in unknown environments is limited, as it lacks the ability to explore unknown regions when blocked by large obstacles. To solve this issue, we introduce Perception-Aware MPPI (PA-MPPI). Here, perception-awareness is defined as adapting the trajectory online based on perception objectives. Specifically, when the goal is occluded, PA-MPPI's perception cost biases trajectories that can perceive unknown regions. This expands the mapped traversable space and increases the likelihood of finding alternative paths to the goal. Through hardware experiments, we demonstrate that PA-MPPI, running at 50 Hz with our efficient perception and mapping module, performs up to 100% better than the baseline in our challenging settings where the state-of-the-art MPPI fails. In addition, we demonstrate that PA-MPPI can be used as a safe and robust action policy for navigation foundation models, which often provide goal poses that are not directly reachable.

Learning on the Fly: Rapid Policy Adaptation via Differentiable Simulation

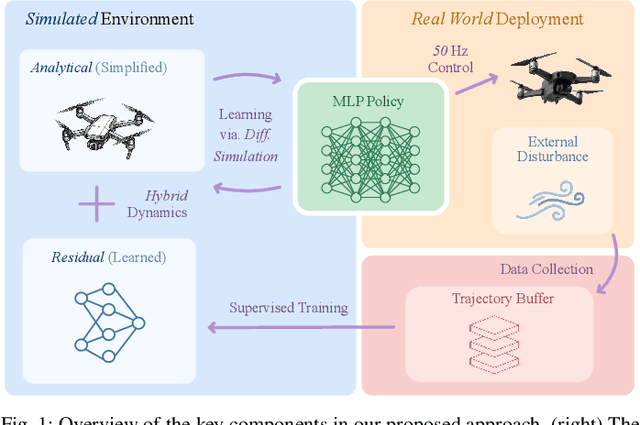
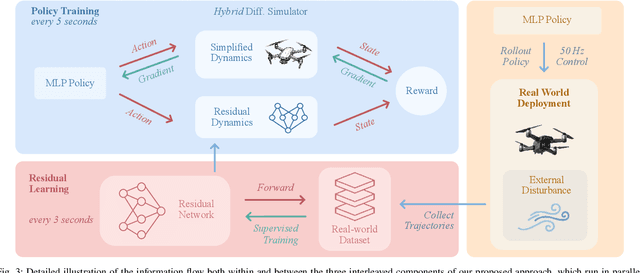
Learning control policies in simulation enables rapid, safe, and cost-effective development of advanced robotic capabilities. However, transferring these policies to the real world remains difficult due to the sim-to-real gap, where unmodeled dynamics and environmental disturbances can degrade policy performance. Existing approaches, such as domain randomization and Real2Sim2Real pipelines, can improve policy robustness, but either struggle under out-of-distribution conditions or require costly offline retraining. In this work, we approach these problems from a different perspective. Instead of relying on diverse training conditions before deployment, we focus on rapidly adapting the learned policy in the real world in an online fashion. To achieve this, we propose a novel online adaptive learning framework that unifies residual dynamics learning with real-time policy adaptation inside a differentiable simulation. Starting from a simple dynamics model, our framework refines the model continuously with real-world data to capture unmodeled effects and disturbances such as payload changes and wind. The refined dynamics model is embedded in a differentiable simulation framework, enabling gradient backpropagation through the dynamics and thus rapid, sample-efficient policy updates beyond the reach of classical RL methods like PPO. All components of our system are designed for rapid adaptation, enabling the policy to adjust to unseen disturbances within 5 seconds of training. We validate the approach on agile quadrotor control under various disturbances in both simulation and the real world. Our framework reduces hovering error by up to 81% compared to L1-MPC and 55% compared to DATT, while also demonstrating robustness in vision-based control without explicit state estimation.

Synthesis of Model Predictive Control and Reinforcement Learning: Survey and Classification

The fields of MPC and RL consider two successful control techniques for Markov decision processes. Both approaches are derived from similar fundamental principles, and both are widely used in practical applications, including robotics, process control, energy systems, and autonomous driving. Despite their similarities, MPC and RL follow distinct paradigms that emerged from diverse communities and different requirements. Various technical discrepancies, particularly the role of an environment model as part of the algorithm, lead to methodologies with nearly complementary advantages. Due to their orthogonal benefits, research interest in combination methods has recently increased significantly, leading to a large and growing set of complex ideas leveraging MPC and RL. This work illuminates the differences, similarities, and fundamentals that allow for different combination algorithms and categorizes existing work accordingly. Particularly, we focus on the versatile actor-critic RL approach as a basis for our categorization and examine how the online optimization approach of MPC can be used to improve the overall closed-loop performance of a policy.

AC4MPC: Actor-Critic Reinforcement Learning for Nonlinear Model Predictive Control

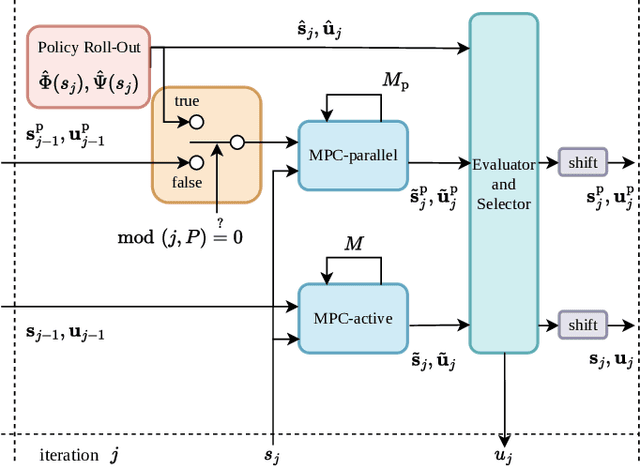
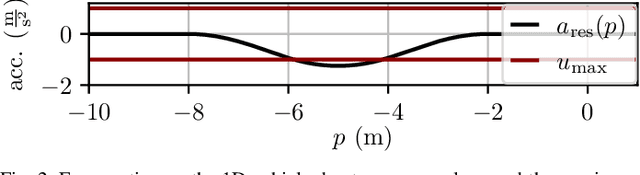
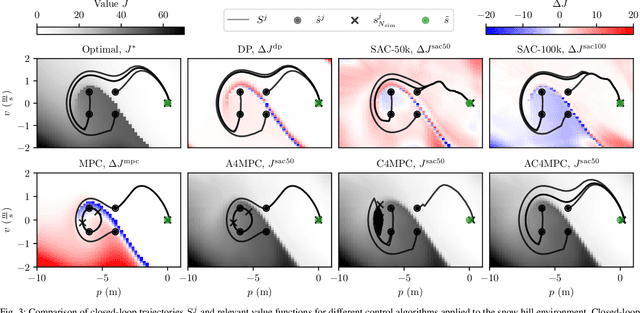
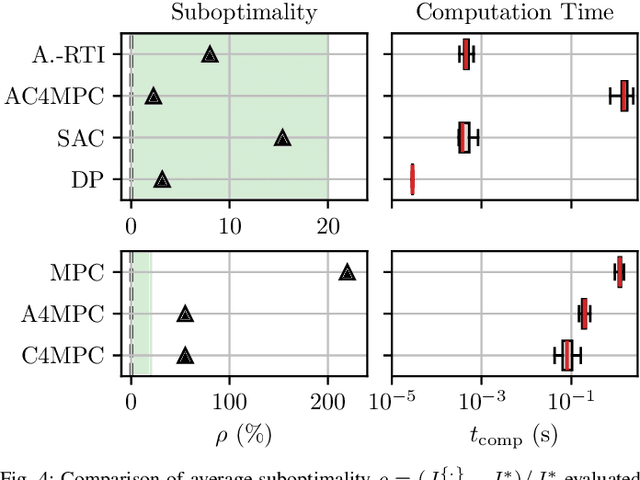
\Ac{MPC} and \ac{RL} are two powerful control strategies with, arguably, complementary advantages. In this work, we show how actor-critic \ac{RL} techniques can be leveraged to improve the performance of \ac{MPC}. The \ac{RL} critic is used as an approximation of the optimal value function, and an actor roll-out provides an initial guess for primal variables of the \ac{MPC}. A parallel control architecture is proposed where each \ac{MPC} instance is solved twice for different initial guesses. Besides the actor roll-out initialization, a shifted initialization from the previous solution is used. Thereafter, the actor and the critic are again used to approximately evaluate the infinite horizon cost of these trajectories. The control actions from the lowest-cost trajectory are applied to the system at each time step. We establish that the proposed algorithm is guaranteed to outperform the original \ac{RL} policy plus an error term that depends on the accuracy of the critic and decays with the horizon length of the \ac{MPC} formulation. Moreover, we do not require globally optimal solutions for these guarantees to hold. The approach is demonstrated on an illustrative toy example and an \ac{AD} overtaking scenario.

Equivariant Deep Learning of Mixed-Integer Optimal Control Solutions for Vehicle Decision Making and Motion Planning

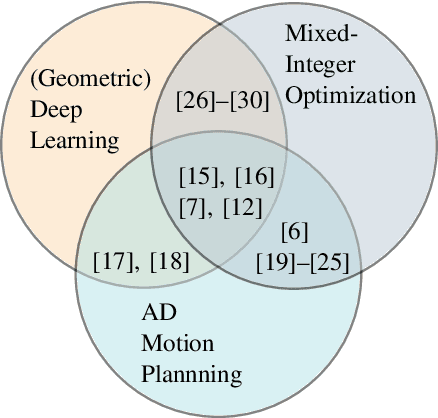
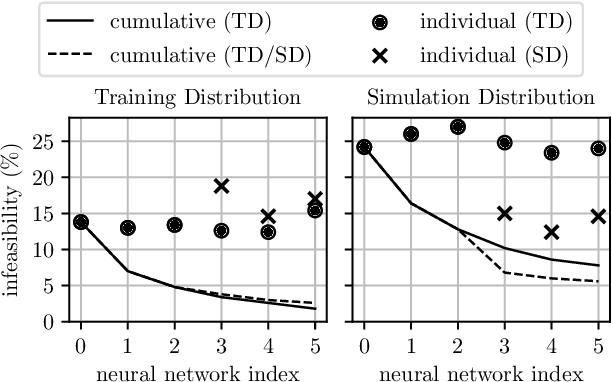
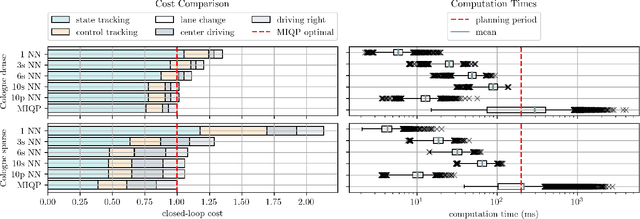
Mixed-integer quadratic programs (MIQPs) are a versatile way of formulating vehicle decision making and motion planning problems, where the prediction model is a hybrid dynamical system that involves both discrete and continuous decision variables. However, even the most advanced MIQP solvers can hardly account for the challenging requirements of automotive embedded platforms. Thus, we use machine learning to simplify and hence speed up optimization. Our work builds on recent ideas for solving MIQPs in real-time by training a neural network to predict the optimal values of integer variables and solving the remaining problem by online quadratic programming. Specifically, we propose a recurrent permutation equivariant deep set that is particularly suited for imitating MIQPs that involve many obstacles, which is often the major source of computational burden in motion planning problems. Our framework comprises also a feasibility projector that corrects infeasible predictions of integer variables and considerably increases the likelihood of computing a collision-free trajectory. We evaluate the performance, safety and real-time feasibility of decision-making for autonomous driving using the proposed approach on realistic multi-lane traffic scenarios with interactive agents in SUMO simulations.

A Long-Short-Term Mixed-Integer Formulation for Highway Lane Change Planning

This work considers the problem of optimal lane changing in a structured multi-agent road environment. A novel motion planning algorithm that can capture long-horizon dependencies as well as short-horizon dynamics is presented. Pivotal to our approach is a geometric approximation of the long-horizon combinatorial transition problem which we formulate in the continuous time-space domain. Moreover, a discrete-time formulation of a short-horizon optimal motion planning problem is formulated and combined with the long-horizon planner. Both individual problems, as well as their combination, are formulated as MIQP and solved in real-time by using state-of-the-art solvers. We show how the presented algorithm outperforms two other state-of-the-art motion planning algorithms in closed-loop performance and computation time in lane changing problems. Evaluations are performed using the traffic simulator SUMO, a custom low-level tracking model predictive controller, and high-fidelity vehicle models and scenarios, provided by the CommonRoad environment.

Frenet-Cartesian Model Representations for Automotive Obstacle Avoidance within Nonlinear MPC

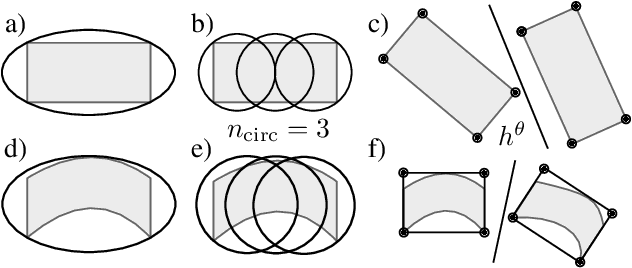
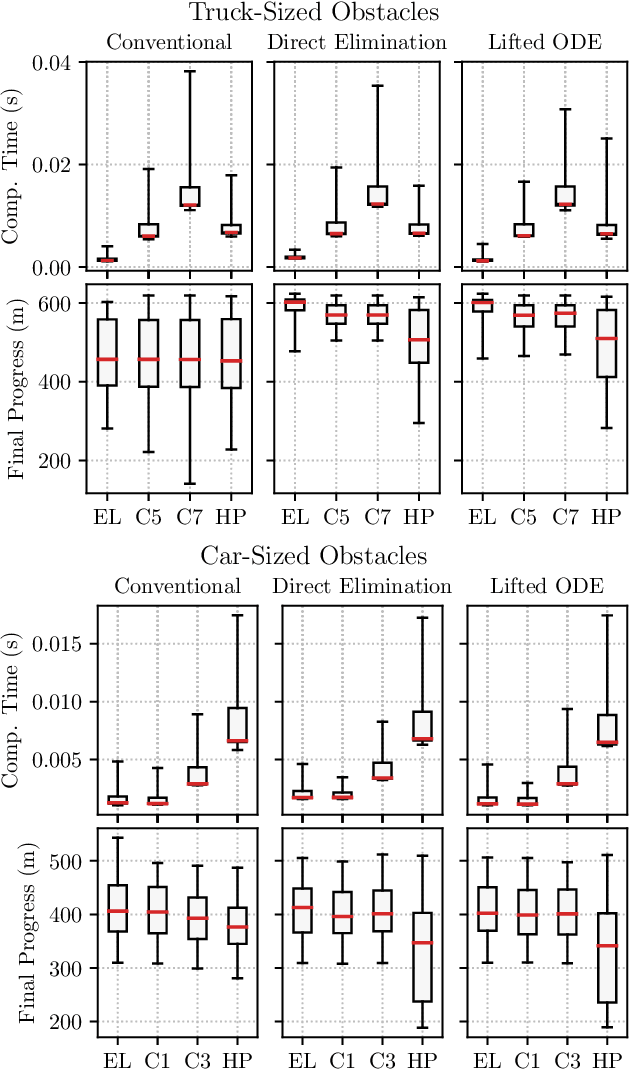
In recent years, nonlinear model predictive control (NMPC) has been extensively used for solving automotive motion control and planning tasks. In order to formulate the NMPC problem, different coordinate systems can be used with different advantages. We propose and compare formulations for the NMPC related optimization problem, involving a Cartesian and a Frenet coordinate frame (CCF/ FCF) in a single nonlinear program (NLP). We specify costs and collision avoidance constraints in the more advantageous coordinate frame, derive appropriate formulations and compare different obstacle constraints. With this approach, we exploit the simpler formulation of opponent vehicle constraints in the CCF, as well as road aligned costs and constraints related to the FCF. Comparisons to other approaches in a simulation framework highlight the advantages of the proposed approaches.

Safe Imitation Learning of Nonlinear Model Predictive Control for Flexible Robots

Flexible robots may overcome the industry's major problems: safe human-robot collaboration and increased load-to-mass ratio. However, oscillations and high dimensional state space complicate the control of flexible robots. This work investigates nonlinear model predictive control (NMPC) of flexible robots -- for simultaneous planning and control -- modeled via the rigid finite element method. Although NMPC performs well in simulation, computational complexity prevents its deployment in practice. We show that imitation learning of NMPC with neural networks as function approximator can massively improve the computation time of the controller at the cost of slight performance loss and, more critically, loss of safety guarantees. We leverage a safety filter formulated as a simpler NMPC to recover safety guarantees. Experiments on a simulated three degrees of freedom flexible robot manipulator demonstrate that the average computational time of the proposed safe approximate NMPC controller is 3.6 ms while of the original NMPC is 11.8 ms. Fast and safe approximate NMPC might facilitate the industry's adoption of flexible robots and new solutions for similar problems, e.g., deformable object manipulation and soft robot control.

A Hierarchical Approach for Strategic Motion Planning in Autonomous Racing

We present an approach for safe trajectory planning, where a strategic task related to autonomous racing is learned sample-efficient within a simulation environment. A high-level policy, represented as a neural network, outputs a reward specification that is used within the cost function of a parametric nonlinear model predictive controller (NMPC). By including constraints and vehicle kinematics in the NLP, we are able to guarantee safe and feasible trajectories related to the used model. Compared to classical reinforcement learning (RL), our approach restricts the exploration to safe trajectories, starts with a good prior performance and yields full trajectories that can be passed to a tracking lowest-level controller. We do not address the lowest-level controller in this work and assume perfect tracking of feasible trajectories. We show the superior performance of our algorithm on simulated racing tasks that include high-level decision making. The vehicle learns to efficiently overtake slower vehicles and to avoid getting overtaken by blocking faster vehicles.