Jonathan Frey
Differentiable Nonlinear Model Predictive Control
May 02, 2025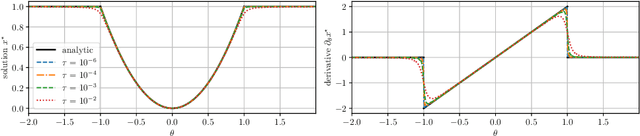

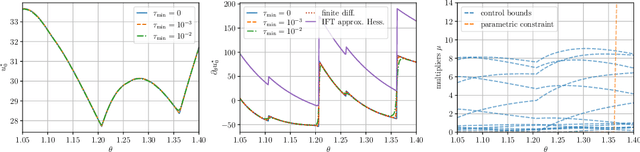

Abstract:The efficient computation of parametric solution sensitivities is a key challenge in the integration of learning-enhanced methods with nonlinear model predictive control (MPC), as their availability is crucial for many learning algorithms. While approaches presented in the machine learning community are limited to convex or unconstrained formulations, this paper discusses the computation of solution sensitivities of general nonlinear programs (NLPs) using the implicit function theorem (IFT) and smoothed optimality conditions treated in interior-point methods (IPM). We detail sensitivity computation within a sequential quadratic programming (SQP) method which employs an IPM for the quadratic subproblems. The publication is accompanied by an efficient open-source implementation within the framework, providing both forward and adjoint sensitivities for general optimal control problems, achieving speedups exceeding 3x over the state-of-the-art solver mpc.pytorch.
Imitation Learning from Nonlinear MPC via the Exact Q-Loss and its Gauss-Newton Approximation
Apr 03, 2023Abstract:This work presents a novel loss function for learning nonlinear Model Predictive Control policies via Imitation Learning. Standard approaches to Imitation Learning neglect information about the expert and generally adopt a loss function based on the distance between expert and learned controls. In this work, we present a loss based on the Q-function directly embedding the performance objectives and constraint satisfaction of the associated Optimal Control Problem (OCP). However, training a Neural Network with the Q-loss requires solving the associated OCP for each new sample. To alleviate the computational burden, we derive a second Q-loss based on the Gauss-Newton approximation of the OCP resulting in a faster training time. We validate our losses against Behavioral Cloning, the standard approach to Imitation Learning, on the control of a nonlinear system with constraints. The final results show that the Q-function-based losses significantly reduce the amount of constraint violations while achieving comparable or better closed-loop costs.
Frenet-Cartesian Model Representations for Automotive Obstacle Avoidance within Nonlinear MPC
Dec 22, 2022

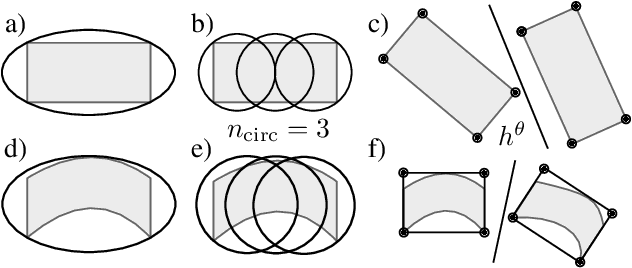
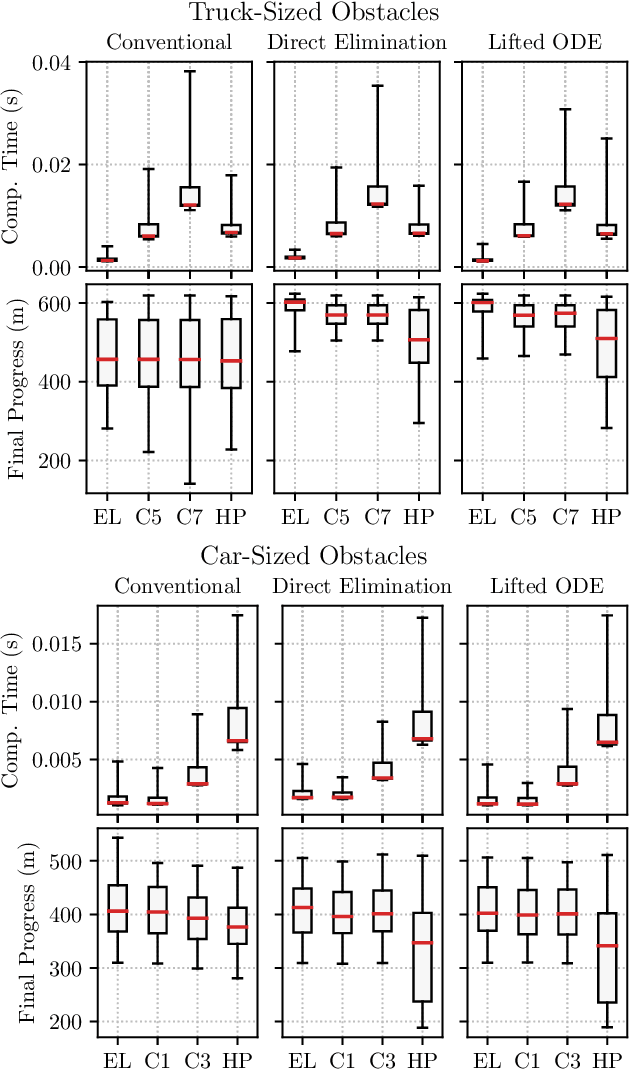
Abstract:In recent years, nonlinear model predictive control (NMPC) has been extensively used for solving automotive motion control and planning tasks. In order to formulate the NMPC problem, different coordinate systems can be used with different advantages. We propose and compare formulations for the NMPC related optimization problem, involving a Cartesian and a Frenet coordinate frame (CCF/ FCF) in a single nonlinear program (NLP). We specify costs and collision avoidance constraints in the more advantageous coordinate frame, derive appropriate formulations and compare different obstacle constraints. With this approach, we exploit the simpler formulation of opponent vehicle constraints in the CCF, as well as road aligned costs and constraints related to the FCF. Comparisons to other approaches in a simulation framework highlight the advantages of the proposed approaches.
Active Learning of Discrete-Time Dynamics for Uncertainty-Aware Model Predictive Control
Oct 23, 2022Abstract:Model-based control requires an accurate model of the system dynamics for precisely and safely controlling the robot in complex and dynamic environments. Moreover, in presence of variations in the operating conditions, the model should be continuously refined to compensate for dynamics changes. In this paper, we propose a self-supervised learning approach to actively model robot discrete-time dynamics. We combine offline learning from past experience and online learning from present robot interaction with the unknown environment. These two ingredients enable highly sample-efficient and adaptive learning for accurate inference of the model dynamics in real-time even in operating regimes significantly different from the training distribution. Moreover, we design an uncertainty-aware model predictive controller that is conditioned to the aleatoric (data) uncertainty of the learned dynamics. The controller actively selects the optimal control actions that (i) optimize the control performance and (ii) boost the online learning sample efficiency. We apply the proposed method to a quadrotor system in multiple challenging real-world experiments. Our approach exhibits high flexibility and generalization capabilities by consistently adapting to unseen flight conditions, while it significantly outperforms classical and adaptive control baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge