Robust Rigid Body Assembly via Contact-Implicit Optimal Control with Exact Second-Order Derivatives

Efficient planning of assembly motions is a long standing challenge in the field of robotics that has been primarily tackled with reinforcement learning and sampling-based methods by using extensive physics simulations. This paper proposes a sample-efficient robust optimal control approach for the determination of assembly motions, which requires significantly less physics simulation steps during planning through the efficient use of derivative information. To this end, a differentiable physics simulation is constructed that provides second-order analytic derivatives to the numerical solver and allows one to traverse seamlessly from informative derivatives to accurate contact simulation. The solution of the physics simulation problem is made differentiable by using smoothing inspired by interior-point methods applied to both the collision detection as well as the contact resolution problem. We propose a modified variant of an optimization-based formulation of collision detection formulated as a linear program and present an efficient implementation for the nominal evaluation and corresponding first- and second-order derivatives. Moreover, a multi-scenario-based trajectory optimization problem that ensures robustness with respect to sim-to-real mismatches is derived. The capability of the considered formulation is illustrated by results where over 99\% successful executions are achieved in real-world experiments. Thereby, we carefully investigate the effect of smooth approximations of the contact dynamics and robust modeling on the success rates. Furthermore, the method's capability is tested on different peg-in-hole problems in simulation to show the benefit of using exact Hessians over commonly used Hessian approximations.

Differentiable Nonlinear Model Predictive Control

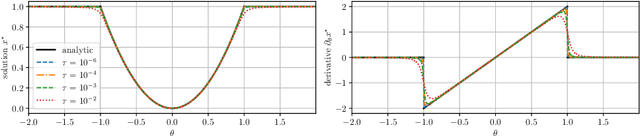
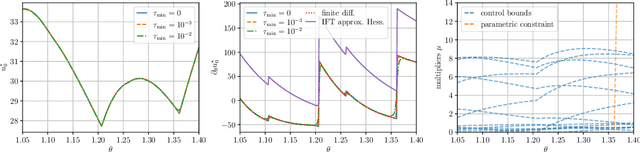
The efficient computation of parametric solution sensitivities is a key challenge in the integration of learning-enhanced methods with nonlinear model predictive control (MPC), as their availability is crucial for many learning algorithms. While approaches presented in the machine learning community are limited to convex or unconstrained formulations, this paper discusses the computation of solution sensitivities of general nonlinear programs (NLPs) using the implicit function theorem (IFT) and smoothed optimality conditions treated in interior-point methods (IPM). We detail sensitivity computation within a sequential quadratic programming (SQP) method which employs an IPM for the quadratic subproblems. The publication is accompanied by an efficient open-source implementation within the framework, providing both forward and adjoint sensitivities for general optimal control problems, achieving speedups exceeding 3x over the state-of-the-art solver mpc.pytorch.

An Efficient Real-Time NMPC for Quadrotor Position Control under Communication Time-Delay

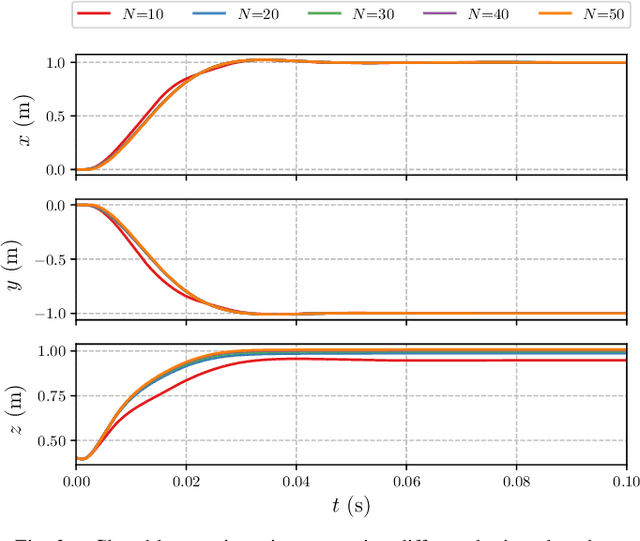
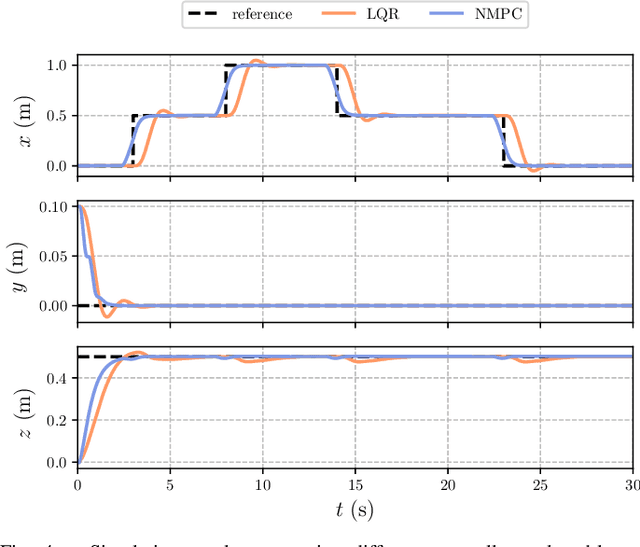
The advances in computer processor technology have enabled the application of nonlinear model predictive control (NMPC) to agile systems, such as quadrotors. These systems are characterized by their underactuation, nonlinearities, bounded inputs, and time-delays. Classical control solutions fall short in overcoming these difficulties and fully exploiting the capabilities offered by such platforms. This paper presents the design and implementation of an efficient position controller for quadrotors based on real-time NMPC with time-delay compensation and bounds enforcement on the actuators. To deal with the limited computational resources onboard, an offboard control architecture is proposed. It is implemented using the high-performance software package acados, which solves optimal control problems and implements a real-time iteration (RTI) variant of a sequential quadratic programming (SQP) scheme with Gauss-Newton Hessian approximation. The quadratic subproblems (QP) in the SQP scheme are solved with HPIPM, an interior-point method solver, built on top of the linear algebra library BLASFEO, finely tuned for multiple CPU architectures. Solution times are further reduced by reformulating the QPs using the efficient partial condensing algorithm implemented in HPIPM. We demonstrate the capabilities of our architecture using the Crazyflie 2.1 nano-quadrotor.