Offline Guarded Safe Reinforcement Learning for Medical Treatment Optimization Strategies

When applying offline reinforcement learning (RL) in healthcare scenarios, the out-of-distribution (OOD) issues pose significant risks, as inappropriate generalization beyond clinical expertise can result in potentially harmful recommendations. While existing methods like conservative Q-learning (CQL) attempt to address the OOD issue, their effectiveness is limited by only constraining action selection by suppressing uncertain actions. This action-only regularization imitates clinician actions that prioritize short-term rewards, but it fails to regulate downstream state trajectories, thereby limiting the discovery of improved long-term treatment strategies. To safely improve policy beyond clinician recommendations while ensuring that state-action trajectories remain in-distribution, we propose \textit{Offline Guarded Safe Reinforcement Learning} ($\mathsf{OGSRL}$), a theoretically grounded model-based offline RL framework. $\mathsf{OGSRL}$ introduces a novel dual constraint mechanism for improving policy with reliability and safety. First, the OOD guardian is established to specify clinically validated regions for safe policy exploration. By constraining optimization within these regions, it enables the reliable exploration of treatment strategies that outperform clinician behavior by leveraging the full patient state history, without drifting into unsupported state-action trajectories. Second, we introduce a safety cost constraint that encodes medical knowledge about physiological safety boundaries, providing domain-specific safeguards even in areas where training data might contain potentially unsafe interventions. Notably, we provide theoretical guarantees on safety and near-optimality: policies that satisfy these constraints remain in safe and reliable regions and achieve performance close to the best possible policy supported by the data.

Differentiable Nonlinear Model Predictive Control

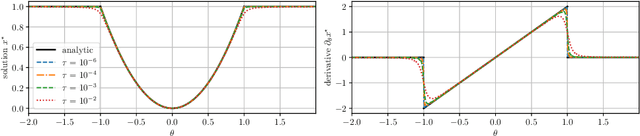
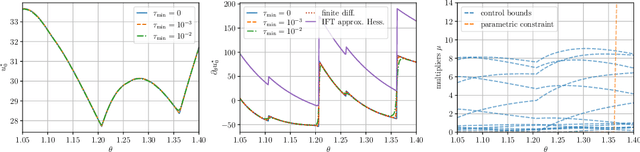
The efficient computation of parametric solution sensitivities is a key challenge in the integration of learning-enhanced methods with nonlinear model predictive control (MPC), as their availability is crucial for many learning algorithms. While approaches presented in the machine learning community are limited to convex or unconstrained formulations, this paper discusses the computation of solution sensitivities of general nonlinear programs (NLPs) using the implicit function theorem (IFT) and smoothed optimality conditions treated in interior-point methods (IPM). We detail sensitivity computation within a sequential quadratic programming (SQP) method which employs an IPM for the quadratic subproblems. The publication is accompanied by an efficient open-source implementation within the framework, providing both forward and adjoint sensitivities for general optimal control problems, achieving speedups exceeding 3x over the state-of-the-art solver mpc.pytorch.

Synthesis of Model Predictive Control and Reinforcement Learning: Survey and Classification

The fields of MPC and RL consider two successful control techniques for Markov decision processes. Both approaches are derived from similar fundamental principles, and both are widely used in practical applications, including robotics, process control, energy systems, and autonomous driving. Despite their similarities, MPC and RL follow distinct paradigms that emerged from diverse communities and different requirements. Various technical discrepancies, particularly the role of an environment model as part of the algorithm, lead to methodologies with nearly complementary advantages. Due to their orthogonal benefits, research interest in combination methods has recently increased significantly, leading to a large and growing set of complex ideas leveraging MPC and RL. This work illuminates the differences, similarities, and fundamentals that allow for different combination algorithms and categorizes existing work accordingly. Particularly, we focus on the versatile actor-critic RL approach as a basis for our categorization and examine how the online optimization approach of MPC can be used to improve the overall closed-loop performance of a policy.

All AI Models are Wrong, but Some are Optimal

AI models that predict the future behavior of a system (a.k.a. predictive AI models) are central to intelligent decision-making. However, decision-making using predictive AI models often results in suboptimal performance. This is primarily because AI models are typically constructed to best fit the data, and hence to predict the most likely future rather than to enable high-performance decision-making. The hope that such prediction enables high-performance decisions is neither guaranteed in theory nor established in practice. In fact, there is increasing empirical evidence that predictive models must be tailored to decision-making objectives for performance. In this paper, we establish formal (necessary and sufficient) conditions that a predictive model (AI-based or not) must satisfy for a decision-making policy established using that model to be optimal. We then discuss their implications for building predictive AI models for sequential decision-making.

Application of Soft Actor-Critic Algorithms in Optimizing Wastewater Treatment with Time Delays Integration

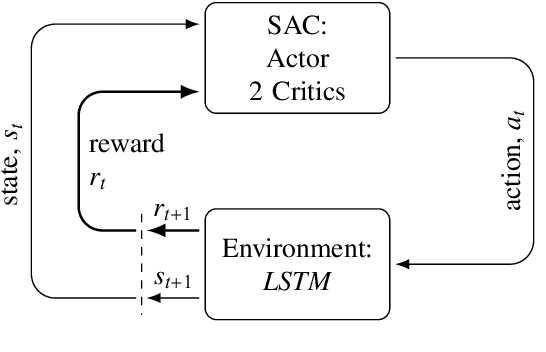
Wastewater treatment plants face unique challenges for process control due to their complex dynamics, slow time constants, and stochastic delays in observations and actions. These characteristics make conventional control methods, such as Proportional-Integral-Derivative controllers, suboptimal for achieving efficient phosphorus removal, a critical component of wastewater treatment to ensure environmental sustainability. This study addresses these challenges using a novel deep reinforcement learning approach based on the Soft Actor-Critic algorithm, integrated with a custom simulator designed to model the delayed feedback inherent in wastewater treatment plants. The simulator incorporates Long Short-Term Memory networks for accurate multi-step state predictions, enabling realistic training scenarios. To account for the stochastic nature of delays, agents were trained under three delay scenarios: no delay, constant delay, and random delay. The results demonstrate that incorporating random delays into the reinforcement learning framework significantly improves phosphorus removal efficiency while reducing operational costs. Specifically, the delay-aware agent achieved 36% reduction in phosphorus emissions, 55% higher reward, 77% lower target deviation from the regulatory limit, and 9% lower total costs than traditional control methods in the simulated environment. These findings underscore the potential of reinforcement learning to overcome the limitations of conventional control strategies in wastewater treatment, providing an adaptive and cost-effective solution for phosphorus removal.

Flipping-based Policy for Chance-Constrained Markov Decision Processes

Safe reinforcement learning (RL) is a promising approach for many real-world decision-making problems where ensuring safety is a critical necessity. In safe RL research, while expected cumulative safety constraints (ECSCs) are typically the first choices, chance constraints are often more pragmatic for incorporating safety under uncertainties. This paper proposes a \textit{flipping-based policy} for Chance-Constrained Markov Decision Processes (CCMDPs). The flipping-based policy selects the next action by tossing a potentially distorted coin between two action candidates. The probability of the flip and the two action candidates vary depending on the state. We establish a Bellman equation for CCMDPs and further prove the existence of a flipping-based policy within the optimal solution sets. Since solving the problem with joint chance constraints is challenging in practice, we then prove that joint chance constraints can be approximated into Expected Cumulative Safety Constraints (ECSCs) and that there exists a flipping-based policy in the optimal solution sets for constrained MDPs with ECSCs. As a specific instance of practical implementations, we present a framework for adapting constrained policy optimization to train a flipping-based policy. This framework can be applied to other safe RL algorithms. We demonstrate that the flipping-based policy can improve the performance of the existing safe RL algorithms under the same limits of safety constraints on Safety Gym benchmarks.

Battery Capacity Knee Identification Using Unsupervised Time Series Segmentation

Capacity knees have been observed in experimental tests of commercial lithium-ion cells of various chemistry types under different operating conditions. Their occurrence can have a significant impact on safety and profitability in battery applications. To address concerns arising from possible knee occurrence in battery applications, this work proposes an algorithm to identify capacity knees as well as their onset from capacity fade curves. The proposed capacity knee identification algorithm is validated on both synthetic degradation data and experimental degradation data of two different battery chemistries, and is also benchmarked to the state-of-the-art knee identification algorithm in the literature. The results demonstrate that our proposed capacity knee identification algorithm could successfully identify capacity knees when the state-of-the-art knee identification algorithm failed. The results can contribute to a better understanding of capacity knees and the proposed capacity knee identification algorithm can be used to, for example, systematically evaluate the knee prediction performance of both model-based methods, and data-driven methods and facilitate better classification of retired automotive batteries from safety and profitability perspectives.

Deep active learning for nonlinear system identification

The exploding research interest for neural networks in modeling nonlinear dynamical systems is largely explained by the networks' capacity to model complex input-output relations directly from data. However, they typically need vast training data before they can be put to any good use. The data generation process for dynamical systems can be an expensive endeavor both in terms of time and resources. Active learning addresses this shortcoming by acquiring the most informative data, thereby reducing the need to collect enormous datasets. What makes the current work unique is integrating the deep active learning framework into nonlinear system identification. We formulate a general static deep active learning acquisition problem for nonlinear system identification. This is enabled by exploring system dynamics locally in different regions of the input space to obtain a simulated dataset covering the broader input space. This simulated dataset can be used in a static deep active learning acquisition scheme referred to as global explorations. The global exploration acquires a batch of initial states corresponding to the most informative state-action trajectories according to a batch acquisition function. The local exploration solves an optimal control problem, finding the control trajectory that maximizes some measure of information. After a batch of informative initial states is acquired, a new round of local explorations from the initial states in the batch is conducted to obtain a set of corresponding control trajectories that are to be applied on the system dynamics to get data from the system. Information measures used in the acquisition scheme are derived from the predictive variance of an ensemble of neural networks. The novel method outperforms standard data acquisition methods used for system identification of nonlinear dynamical systems in the case study performed on simulated data.

Learning-based MPC from Big Data Using Reinforcement Learning

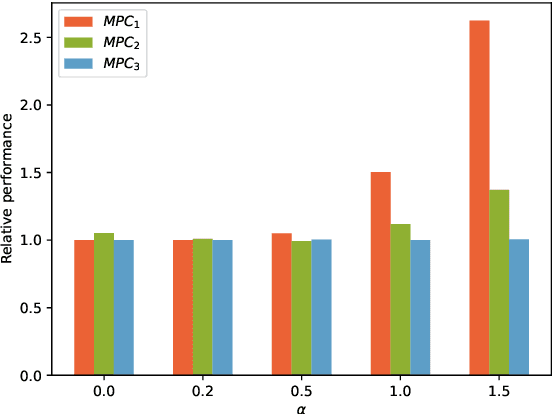
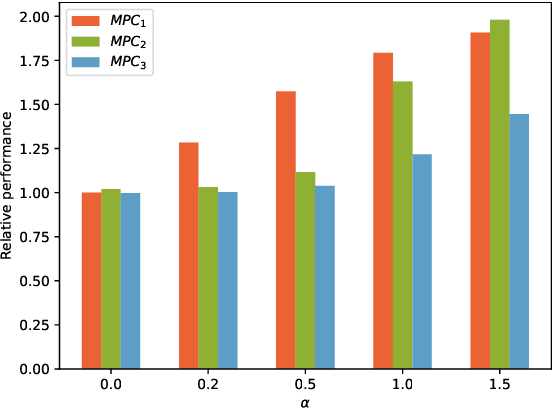
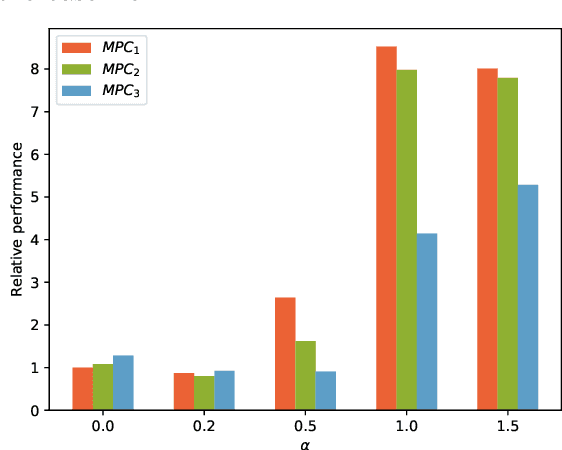
This paper presents an approach for learning Model Predictive Control (MPC) schemes directly from data using Reinforcement Learning (RL) methods. The state-of-the-art learning methods use RL to improve the performance of parameterized MPC schemes. However, these learning algorithms are often gradient-based methods that require frequent evaluations of computationally expensive MPC schemes, thereby restricting their use on big datasets. We propose to tackle this issue by using tools from RL to learn a parameterized MPC scheme directly from data in an offline fashion. Our approach derives an MPC scheme without having to solve it over the collected dataset, thereby eliminating the computational complexity of existing techniques for big data. We evaluate the proposed method on three simulated experiments of varying complexity.

Bridging the gap between QP-based and MPC-based RL

Reinforcement learning methods typically use Deep Neural Networks to approximate the value functions and policies underlying a Markov Decision Process. Unfortunately, DNN-based RL suffers from a lack of explainability of the resulting policy. In this paper, we instead approximate the policy and value functions using an optimization problem, taking the form of Quadratic Programs (QPs). We propose simple tools to promote structures in the QP, pushing it to resemble a linear MPC scheme. A generic unstructured QP offers high flexibility for learning, while a QP having the structure of an MPC scheme promotes the explainability of the resulting policy, additionally provides ways for its analysis. The tools we propose allow for continuously adjusting the trade-off between the former and the latter during learning. We illustrate the workings of our proposed method with the resulting structure using a point-mass task.