Direct transfer of optimized controllers to similar systems using dimensionless MPC

Scaled model experiments are commonly used in various engineering fields to reduce experimentation costs and overcome constraints associated with full-scale systems. The relevance of such experiments relies on dimensional analysis and the principle of dynamic similarity. However, transferring controllers to full-scale systems often requires additional tuning. In this paper, we propose a method to enable a direct controller transfer using dimensionless model predictive control, tuned automatically for closed-loop performance. With this reformulation, the closed-loop behavior of an optimized controller transfers directly to a new, dynamically similar system. Additionally, the dimensionless formulation allows for the use of data from systems of different scales during parameter optimization. We demonstrate the method on a cartpole swing-up and a car racing problem, applying either reinforcement learning or Bayesian optimization for tuning the controller parameters. Software used to obtain the results in this paper is publicly available at https://github.com/josipkh/dimensionless-mpcrl.

All AI Models are Wrong, but Some are Optimal

AI models that predict the future behavior of a system (a.k.a. predictive AI models) are central to intelligent decision-making. However, decision-making using predictive AI models often results in suboptimal performance. This is primarily because AI models are typically constructed to best fit the data, and hence to predict the most likely future rather than to enable high-performance decision-making. The hope that such prediction enables high-performance decisions is neither guaranteed in theory nor established in practice. In fact, there is increasing empirical evidence that predictive models must be tailored to decision-making objectives for performance. In this paper, we establish formal (necessary and sufficient) conditions that a predictive model (AI-based or not) must satisfy for a decision-making policy established using that model to be optimal. We then discuss their implications for building predictive AI models for sequential decision-making.

Learning-based MPC from Big Data Using Reinforcement Learning

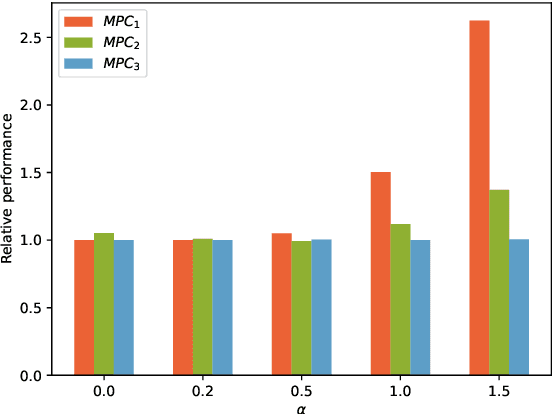
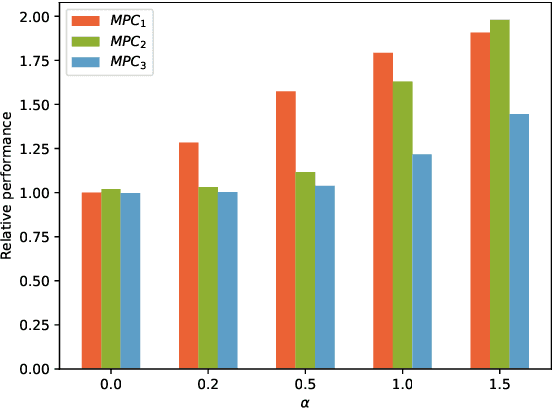
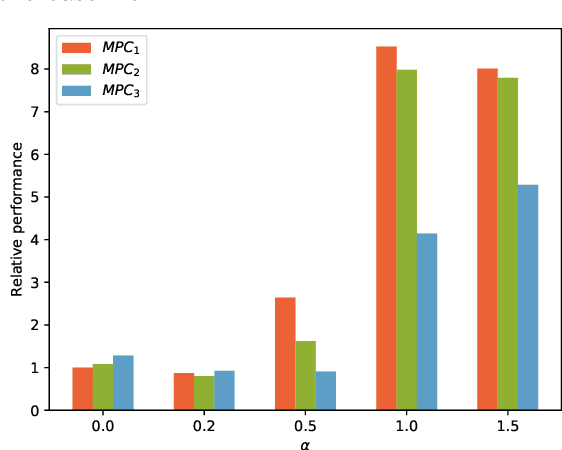
This paper presents an approach for learning Model Predictive Control (MPC) schemes directly from data using Reinforcement Learning (RL) methods. The state-of-the-art learning methods use RL to improve the performance of parameterized MPC schemes. However, these learning algorithms are often gradient-based methods that require frequent evaluations of computationally expensive MPC schemes, thereby restricting their use on big datasets. We propose to tackle this issue by using tools from RL to learn a parameterized MPC scheme directly from data in an offline fashion. Our approach derives an MPC scheme without having to solve it over the collected dataset, thereby eliminating the computational complexity of existing techniques for big data. We evaluate the proposed method on three simulated experiments of varying complexity.

Bridging the gap between QP-based and MPC-based RL

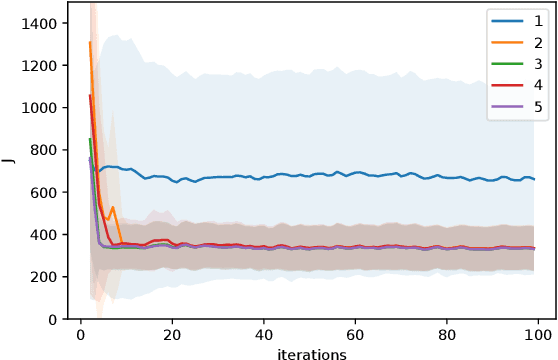
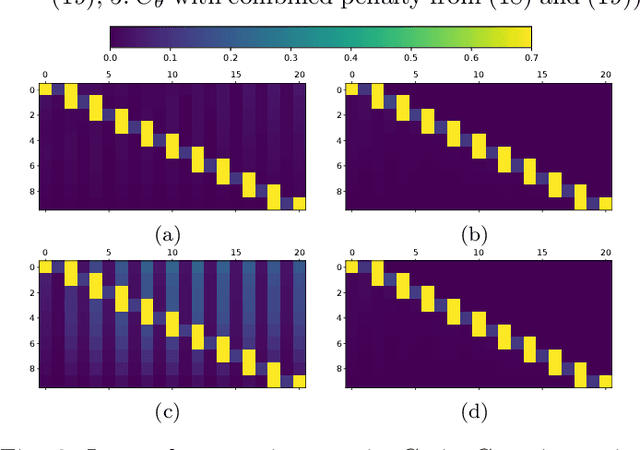
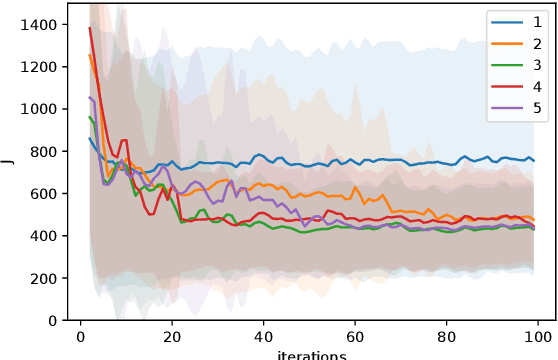
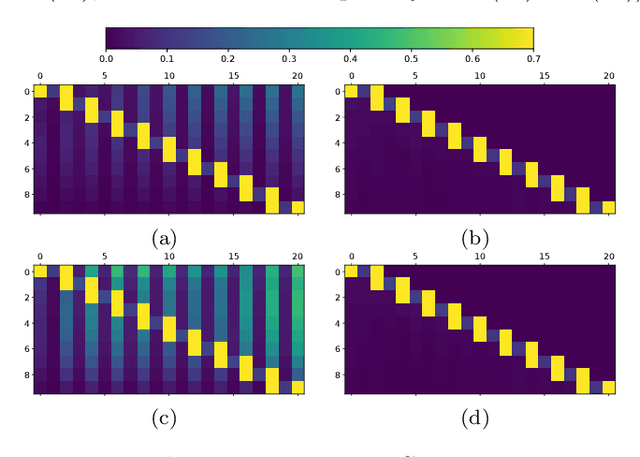
Reinforcement learning methods typically use Deep Neural Networks to approximate the value functions and policies underlying a Markov Decision Process. Unfortunately, DNN-based RL suffers from a lack of explainability of the resulting policy. In this paper, we instead approximate the policy and value functions using an optimization problem, taking the form of Quadratic Programs (QPs). We propose simple tools to promote structures in the QP, pushing it to resemble a linear MPC scheme. A generic unstructured QP offers high flexibility for learning, while a QP having the structure of an MPC scheme promotes the explainability of the resulting policy, additionally provides ways for its analysis. The tools we propose allow for continuously adjusting the trade-off between the former and the latter during learning. We illustrate the workings of our proposed method with the resulting structure using a point-mass task.

Sample-efficient Cross-Entropy Method for Real-time Planning

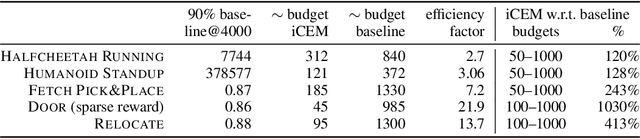
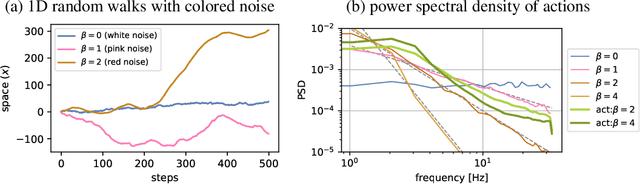
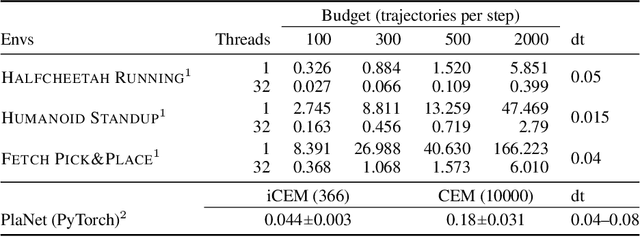
Trajectory optimizers for model-based reinforcement learning, such as the Cross-Entropy Method (CEM), can yield compelling results even in high-dimensional control tasks and sparse-reward environments. However, their sampling inefficiency prevents them from being used for real-time planning and control. We propose an improved version of the CEM algorithm for fast planning, with novel additions including temporally-correlated actions and memory, requiring 2.7-22x less samples and yielding a performance increase of 1.2-10x in high-dimensional control problems.