Making Higher Order MOT Scalable: An Efficient Approximate Solver for Lifted Disjoint Paths

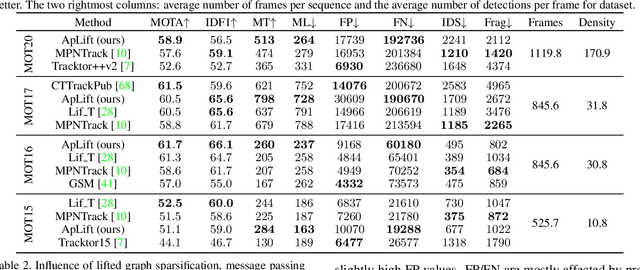
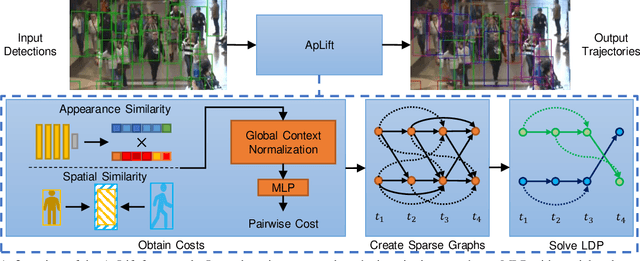
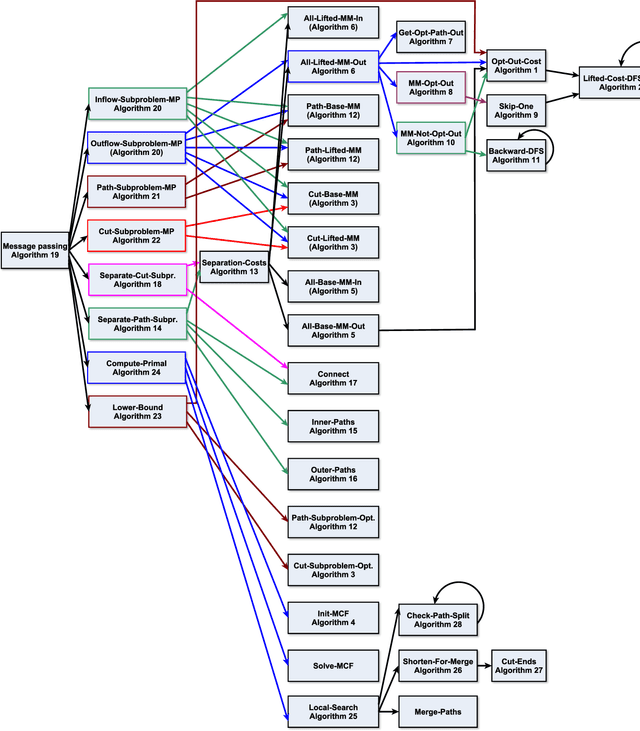
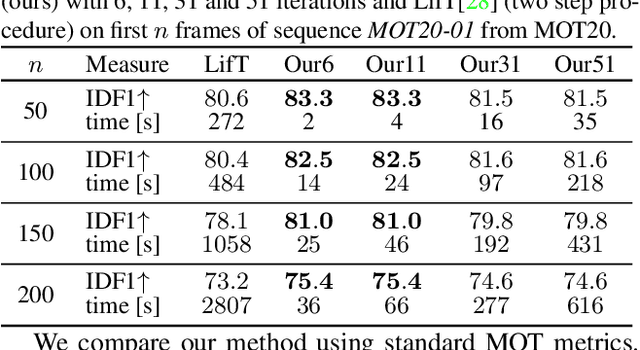
We present an efficient approximate message passing solver for the lifted disjoint paths problem (LDP), a natural but NP-hard model for multiple object tracking (MOT). Our tracker scales to very large instances that come from long and crowded MOT sequences. Our approximate solver enables us to process the MOT15/16/17 benchmarks without sacrificing solution quality and allows for solving MOT20, which has been out of reach up to now for LDP solvers due to its size and complexity. On all these four standard MOT benchmarks we achieve performance comparable or better than current state-of-the-art methods including a tracker based on an optimal LDP solver.

Demystifying Inductive Biases for $β$-VAE Based Architectures

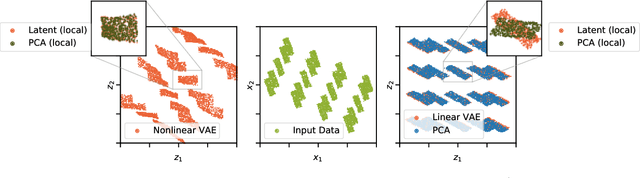
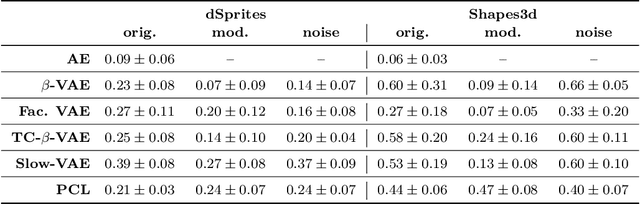
The performance of $\beta$-Variational-Autoencoders ($\beta$-VAEs) and their variants on learning semantically meaningful, disentangled representations is unparalleled. On the other hand, there are theoretical arguments suggesting the impossibility of unsupervised disentanglement. In this work, we shed light on the inductive bias responsible for the success of VAE-based architectures. We show that in classical datasets the structure of variance, induced by the generating factors, is conveniently aligned with the latent directions fostered by the VAE objective. This builds the pivotal bias on which the disentangling abilities of VAEs rely. By small, elaborate perturbations of existing datasets, we hide the convenient correlation structure that is easily exploited by a variety of architectures. To demonstrate this, we construct modified versions of standard datasets in which (i) the generative factors are perfectly preserved; (ii) each image undergoes a mild transformation causing a small change of variance; (iii) the leading \textbf{VAE-based disentanglement architectures fail to produce disentangled representations whilst the performance of a non-variational method remains unchanged}. The construction of our modifications is nontrivial and relies on recent progress on mechanistic understanding of $\beta$-VAEs and their connection to PCA. We strengthen that connection by providing additional insights that are of stand-alone interest.

Sample-efficient Cross-Entropy Method for Real-time Planning

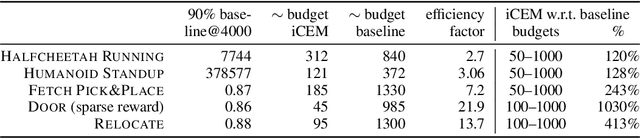
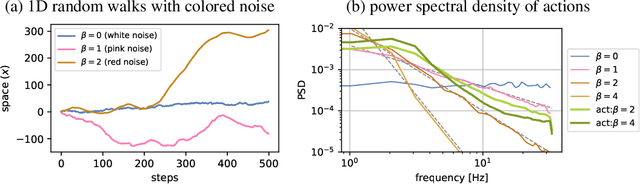
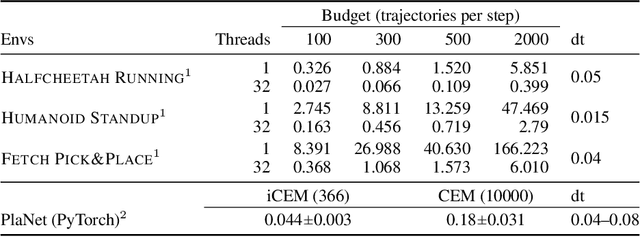
Trajectory optimizers for model-based reinforcement learning, such as the Cross-Entropy Method (CEM), can yield compelling results even in high-dimensional control tasks and sparse-reward environments. However, their sampling inefficiency prevents them from being used for real-time planning and control. We propose an improved version of the CEM algorithm for fast planning, with novel additions including temporally-correlated actions and memory, requiring 2.7-22x less samples and yielding a performance increase of 1.2-10x in high-dimensional control problems.

Variational Autoencoders Pursue PCA Directions (by Accident)

The Variational Autoencoder (VAE) is a powerful architecture capable of representation learning and generative modeling. When it comes to learning interpretable (disentangled) representations, VAE and its variants show unparalleled performance. However, the reasons for this are unclear, since a very particular alignment of the latent embedding is needed but the design of the VAE does not encourage it in any explicit way. We address this matter and offer the following explanation: the diagonal approximation in the encoder together with the inherent stochasticity force local orthogonality of the decoder. The local behavior of promoting both reconstruction and orthogonality matches closely how the PCA embedding is chosen. Alongside providing an intuitive understanding, we justify the statement with full theoretical analysis as well as with experiments.

L4: Practical loss-based stepsize adaptation for deep learning

We propose a stepsize adaptation scheme for stochastic gradient descent. It operates directly with the loss function and rescales the gradient in order to make fixed predicted progress on the loss. We demonstrate its capabilities by conclusively improving the performance of Adam and Momentum optimizers. The enhanced optimizers with default hyperparameters consistently outperform their constant stepsize counterparts, even the best ones, without a measurable increase in computational cost. The performance is validated on multiple architectures including dense nets, CNNs, ResNets, and the recurrent Differential Neural Computer on classical datasets MNIST, fashion MNIST, CIFAR10 and others.

Efficient Optimization for Rank-based Loss Functions

The accuracy of information retrieval systems is often measured using complex loss functions such as the average precision (AP) or the normalized discounted cumulative gain (NDCG). Given a set of positive and negative samples, the parameters of a retrieval system can be estimated by minimizing these loss functions. However, the non-differentiability and non-decomposability of these loss functions does not allow for simple gradient based optimization algorithms. This issue is generally circumvented by either optimizing a structured hinge-loss upper bound to the loss function or by using asymptotic methods like the direct-loss minimization framework. Yet, the high computational complexity of loss-augmented inference, which is necessary for both the frameworks, prohibits its use in large training data sets. To alleviate this deficiency, we present a novel quicksort flavored algorithm for a large class of non-decomposable loss functions. We provide a complete characterization of the loss functions that are amenable to our algorithm, and show that it includes both AP and NDCG based loss functions. Furthermore, we prove that no comparison based algorithm can improve upon the computational complexity of our approach asymptotically. We demonstrate the effectiveness of our approach in the context of optimizing the structured hinge loss upper bound of AP and NDCG loss for learning models for a variety of vision tasks. We show that our approach provides significantly better results than simpler decomposable loss functions, while requiring a comparable training time.

Total variation on a tree

We consider the problem of minimizing the continuous valued total variation subject to different unary terms on trees and propose fast direct algorithms based on dynamic programming to solve these problems. We treat both the convex and the non-convex case and derive worst case complexities that are equal or better than existing methods. We show applications to total variation based 2D image processing and computer vision problems based on a Lagrangian decomposition approach. The resulting algorithms are very efficient, offer a high degree of parallelism and come along with memory requirements which are only in the order of the number of image pixels.