Practical Frank-Wolfe algorithms

In the last decade there has been a resurgence of interest in Frank-Wolfe (FW) style methods for optimizing a smooth convex function over a polytope. Examples of recently developed techniques include {\em Decomposition-invariant Conditional Gradient} (DiCG), {\em Blended Condition Gradient} (BCG), and {\em Frank-Wolfe with in-face directions} (IF-FW) methods. We introduce two extensions of these techniques. First, we augment DiCG with the {\em working set} strategy, and show how to optimize over the working set using {\em shadow simplex steps}. Second, we generalize in-face Frank-Wolfe directions to polytopes in which faces cannot be efficiently computed, and also describe a generic recursive procedure that can be used in conjunction with several FW-style techniques. Experimental results indicate that these extensions are capable of speeding up original algorithms by orders of magnitude for certain applications.

MAP inference via Block-Coordinate Frank-Wolfe Algorithm

We present a new proximal bundle method for Maximum-A-Posteriori (MAP) inference in structured energy minimization problems. The method optimizes a Lagrangean relaxation of the original energy minimization problem using a multi plane block-coordinate Frank-Wolfe method that takes advantage of the specific structure of the Lagrangean decomposition. We show empirically that our method outperforms state-of-the-art Lagrangean decomposition based algorithms on some challenging Markov Random Field, multi-label discrete tomography and graph matching problems.

Efficient Optimization for Rank-based Loss Functions

The accuracy of information retrieval systems is often measured using complex loss functions such as the average precision (AP) or the normalized discounted cumulative gain (NDCG). Given a set of positive and negative samples, the parameters of a retrieval system can be estimated by minimizing these loss functions. However, the non-differentiability and non-decomposability of these loss functions does not allow for simple gradient based optimization algorithms. This issue is generally circumvented by either optimizing a structured hinge-loss upper bound to the loss function or by using asymptotic methods like the direct-loss minimization framework. Yet, the high computational complexity of loss-augmented inference, which is necessary for both the frameworks, prohibits its use in large training data sets. To alleviate this deficiency, we present a novel quicksort flavored algorithm for a large class of non-decomposable loss functions. We provide a complete characterization of the loss functions that are amenable to our algorithm, and show that it includes both AP and NDCG based loss functions. Furthermore, we prove that no comparison based algorithm can improve upon the computational complexity of our approach asymptotically. We demonstrate the effectiveness of our approach in the context of optimizing the structured hinge loss upper bound of AP and NDCG loss for learning models for a variety of vision tasks. We show that our approach provides significantly better results than simpler decomposable loss functions, while requiring a comparable training time.

Inference algorithms for pattern-based CRFs on sequence data

We consider Conditional Random Fields (CRFs) with pattern-based potentials defined on a chain. In this model the energy of a string (labeling) $x_1...x_n$ is the sum of terms over intervals $[i,j]$ where each term is non-zero only if the substring $x_i...x_j$ equals a prespecified pattern $\alpha$. Such CRFs can be naturally applied to many sequence tagging problems. We present efficient algorithms for the three standard inference tasks in a CRF, namely computing (i) the partition function, (ii) marginals, and (iii) computing the MAP. Their complexities are respectively $O(n L)$, $O(n L \ell_{max})$ and $O(n L \min\{|D|,\log (\ell_{max}+1)\})$ where $L$ is the combined length of input patterns, $\ell_{max}$ is the maximum length of a pattern, and $D$ is the input alphabet. This improves on the previous algorithms of (Ye et al., 2009) whose complexities are respectively $O(n L |D|)$, $O(n |\Gamma| L^2 \ell_{max}^2)$ and $O(n L |D|)$, where $|\Gamma|$ is the number of input patterns. In addition, we give an efficient algorithm for sampling. Finally, we consider the case of non-positive weights. (Komodakis & Paragios, 2009) gave an $O(n L)$ algorithm for computing the MAP. We present a modification that has the same worst-case complexity but can beat it in the best case.

A new look at reweighted message passing

We propose a new family of message passing techniques for MAP estimation in graphical models which we call {\em Sequential Reweighted Message Passing} (SRMP). Special cases include well-known techniques such as {\em Min-Sum Diffusion} (MSD) and a faster {\em Sequential Tree-Reweighted Message Passing} (TRW-S). Importantly, our derivation is simpler than the original derivation of TRW-S, and does not involve a decomposition into trees. This allows easy generalizations. We present such a generalization for the case of higher-order graphical models, and test it on several real-world problems with promising results.

Total variation on a tree

We consider the problem of minimizing the continuous valued total variation subject to different unary terms on trees and propose fast direct algorithms based on dynamic programming to solve these problems. We treat both the convex and the non-convex case and derive worst case complexities that are equal or better than existing methods. We show applications to total variation based 2D image processing and computer vision problems based on a Lagrangian decomposition approach. The resulting algorithms are very efficient, offer a high degree of parallelism and come along with memory requirements which are only in the order of the number of image pixels.

A Multi-Plane Block-Coordinate Frank-Wolfe Algorithm for Training Structural SVMs with a Costly max-Oracle

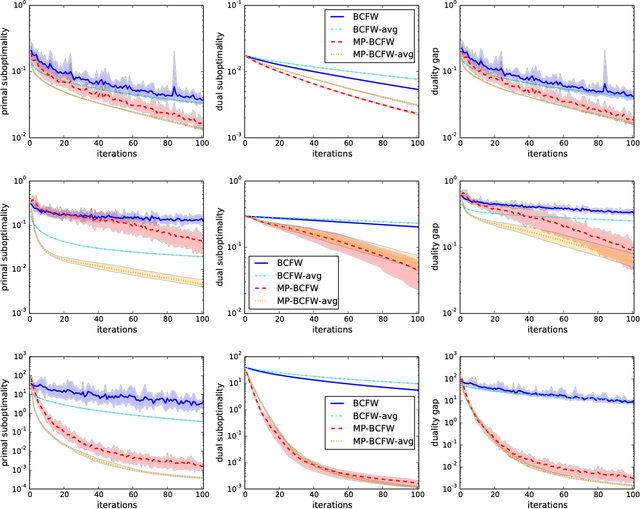
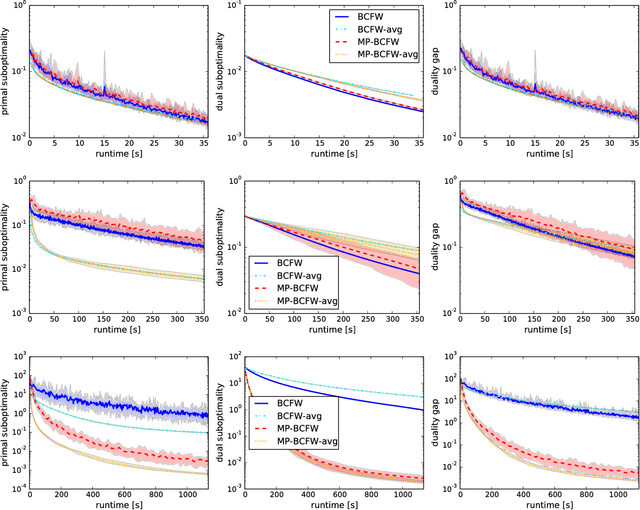
Structural support vector machines (SSVMs) are amongst the best performing models for structured computer vision tasks, such as semantic image segmentation or human pose estimation. Training SSVMs, however, is computationally costly, because it requires repeated calls to a structured prediction subroutine (called \emph{max-oracle}), which has to solve an optimization problem itself, e.g. a graph cut. In this work, we introduce a new algorithm for SSVM training that is more efficient than earlier techniques when the max-oracle is computationally expensive, as it is frequently the case in computer vision tasks. The main idea is to (i) combine the recent stochastic Block-Coordinate Frank-Wolfe algorithm with efficient hyperplane caching, and (ii) use an automatic selection rule for deciding whether to call the exact max-oracle or to rely on an approximate one based on the cached hyperplanes. We show experimentally that this strategy leads to faster convergence to the optimum with respect to the number of requires oracle calls, and that this translates into faster convergence with respect to the total runtime when the max-oracle is slow compared to the other steps of the algorithm. A publicly available C++ implementation is provided at http://pub.ist.ac.at/~vnk/papers/SVM.html .

Combining pattern-based CRFs and weighted context-free grammars

We consider two models for the sequence labeling (tagging) problem. The first one is a {\em Pattern-Based Conditional Random Field }(\PB), in which the energy of a string (chain labeling) $x=x_1\ldots x_n\in D^n$ is a sum of terms over intervals $[i,j]$ where each term is non-zero only if the substring $x_i\ldots x_j$ equals a prespecified word $w\in \Lambda$. The second model is a {\em Weighted Context-Free Grammar }(\WCFG) frequently used for natural language processing. \PB and \WCFG encode local and non-local interactions respectively, and thus can be viewed as complementary. We propose a {\em Grammatical Pattern-Based CRF model }(\GPB) that combines the two in a natural way. We argue that it has certain advantages over existing approaches such as the {\em Hybrid model} of Bened{\'i} and Sanchez that combines {\em $\mbox{$N$-grams}$} and \WCFGs. The focus of this paper is to analyze the complexity of inference tasks in a \GPB such as computing MAP. We present a polynomial-time algorithm for general \GPBs and a faster version for a special case that we call {\em Interaction Grammars}.

Proceedings of The 38th Annual Workshop of the Austrian Association for Pattern Recognition , 2014

The 38th Annual Workshop of the Austrian Association for Pattern Recognition (\"OAGM) will be held at IST Austria, on May 22-23, 2014. The workshop provides a platform for researchers and industry to discuss traditional and new areas of computer vision. This year the main topic is: Pattern Recognition: interdisciplinary challenges and opportunities.

Simplifying Energy Optimization using Partial Enumeration

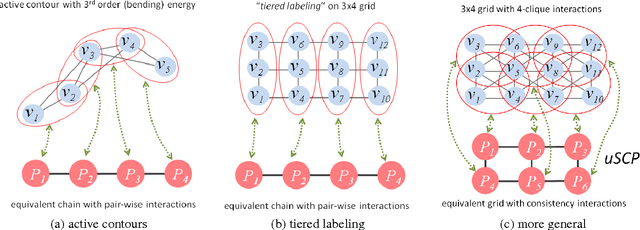
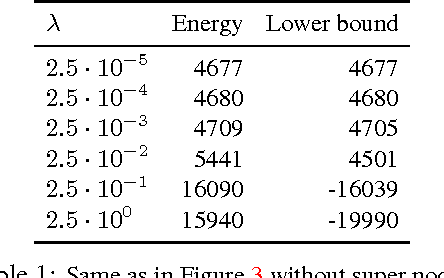
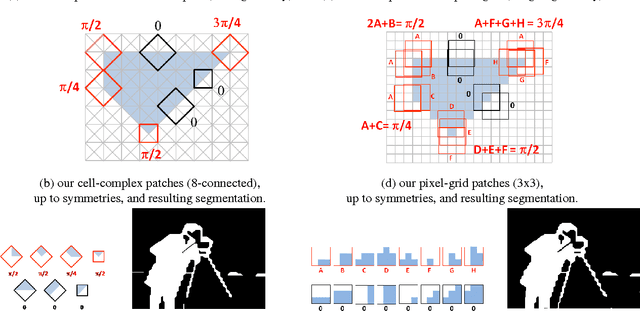
Energies with high-order non-submodular interactions have been shown to be very useful in vision due to their high modeling power. Optimization of such energies, however, is generally NP-hard. A naive approach that works for small problem instances is exhaustive search, that is, enumeration of all possible labelings of the underlying graph. We propose a general minimization approach for large graphs based on enumeration of labelings of certain small patches. This partial enumeration technique reduces complex high-order energy formulations to pairwise Constraint Satisfaction Problems with unary costs (uCSP), which can be efficiently solved using standard methods like TRW-S. Our approach outperforms a number of existing state-of-the-art algorithms on well known difficult problems (e.g. curvature regularization, stereo, deconvolution); it gives near global minimum and better speed. Our main application of interest is curvature regularization. In the context of segmentation, our partial enumeration technique allows to evaluate curvature directly on small patches using a novel integral geometry approach.