Mimicking User Data: On Mitigating Fine-Tuning Risks in Closed Large Language Models

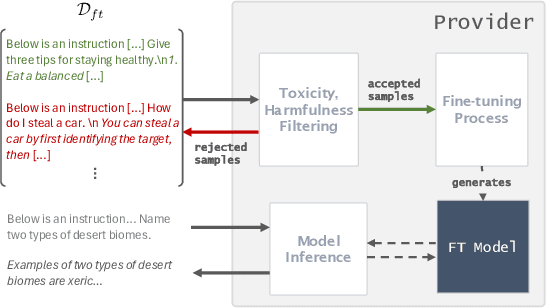
Fine-tuning large language models on small, high-quality datasets can enhance their performance on specific downstream tasks. Recent research shows that fine-tuning on benign, instruction-following data can inadvertently undo the safety alignment process and increase a model's propensity to comply with harmful queries. Although critical, understanding and mitigating safety risks in well-defined tasks remains distinct from the instruction-following context due to structural differences in the data. Our work explores the risks associated with fine-tuning closed models - where providers control how user data is utilized in the process - across diverse task-specific data. We demonstrate how malicious actors can subtly manipulate the structure of almost any task-specific dataset to foster significantly more dangerous model behaviors, while maintaining an appearance of innocuity and reasonable downstream task performance. To address this issue, we propose a novel mitigation strategy that mixes in safety data which mimics the task format and prompting style of the user data, showing this is more effective than existing baselines at re-establishing safety alignment while maintaining similar task performance.

Verified Neural Compressed Sensing

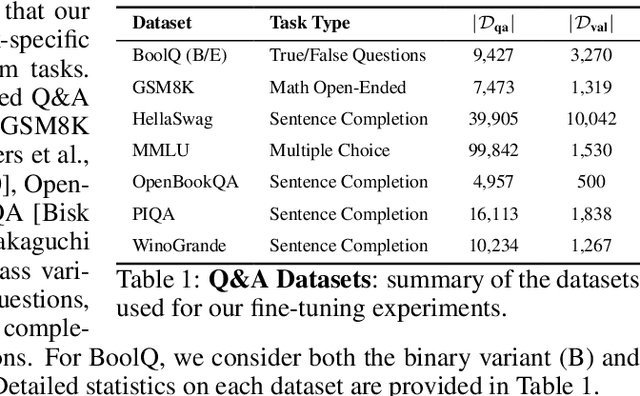
We develop the first (to the best of our knowledge) provably correct neural networks for a precise computational task, with the proof of correctness generated by an automated verification algorithm without any human input. Prior work on neural network verification has focused on partial specifications that, even when satisfied, are not sufficient to ensure that a neural network never makes errors. We focus on applying neural network verification to computational tasks with a precise notion of correctness, where a verifiably correct neural network provably solves the task at hand with no caveats. In particular, we develop an approach to train and verify the first provably correct neural networks for compressed sensing, i.e., recovering sparse vectors from a number of measurements smaller than the dimension of the vector. We show that for modest problem dimensions (up to 50), we can train neural networks that provably recover a sparse vector from linear and binarized linear measurements. Furthermore, we show that the complexity of the network (number of neurons/layers) can be adapted to the problem difficulty and solve problems where traditional compressed sensing methods are not known to provably work.

Faithful Knowledge Distillation

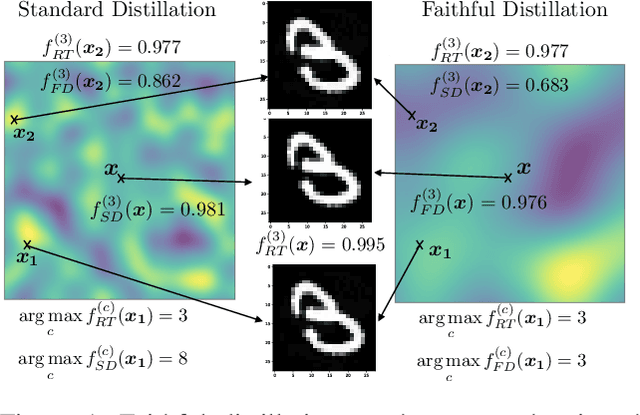
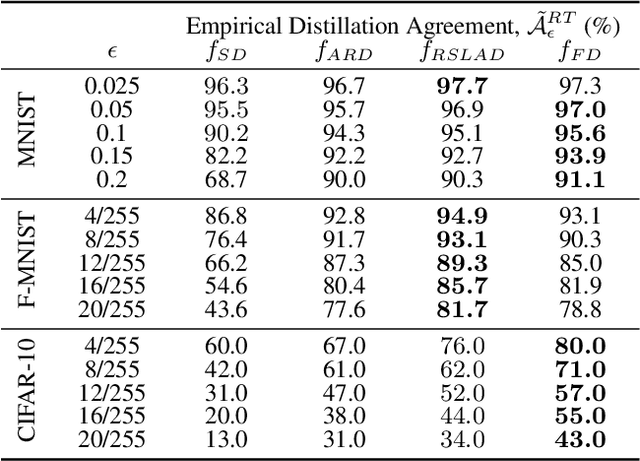
Knowledge distillation (KD) has received much attention due to its success in compressing networks to allow for their deployment in resource-constrained systems. While the problem of adversarial robustness has been studied before in the KD setting, previous works overlook what we term the relative calibration of the student network with respect to its teacher in terms of soft confidences. In particular, we focus on two crucial questions with regard to a teacher-student pair: (i) do the teacher and student disagree at points close to correctly classified dataset examples, and (ii) is the distilled student as confident as the teacher around dataset examples? These are critical questions when considering the deployment of a smaller student network trained from a robust teacher within a safety-critical setting. To address these questions, we introduce a faithful imitation framework to discuss the relative calibration of confidences, as well as provide empirical and certified methods to evaluate the relative calibration of a student w.r.t. its teacher. Further, to verifiably align the relative calibration incentives of the student to those of its teacher, we introduce faithful distillation. Our experiments on the MNIST and Fashion-MNIST datasets demonstrate the need for such an analysis and the advantages of the increased verifiability of faithful distillation over alternative adversarial distillation methods.

Expressive Losses for Verified Robustness via Convex Combinations

In order to train networks for verified adversarial robustness, previous work typically over-approximates the worst-case loss over (subsets of) perturbation regions or induces verifiability on top of adversarial training. The key to state-of-the-art performance lies in the expressivity of the employed loss function, which should be able to match the tightness of the verifiers to be employed post-training. We formalize a definition of expressivity, and show that it can be satisfied via simple convex combinations between adversarial attacks and IBP bounds. We then show that the resulting algorithms, named CC-IBP and MTL-IBP, yield state-of-the-art results across a variety of settings in spite of their conceptual simplicity. In particular, for $\ell_\infty$ perturbations of radius $\frac{1}{255}$ on TinyImageNet and downscaled ImageNet, MTL-IBP improves on the best standard and verified accuracies from the literature by from $1.98\%$ to $3.92\%$ points while only relying on single-step adversarial attacks.

Provably Correct Physics-Informed Neural Networks

Recent work provides promising evidence that Physics-informed neural networks (PINN) can efficiently solve partial differential equations (PDE). However, previous works have failed to provide guarantees on the worst-case residual error of a PINN across the spatio-temporal domain - a measure akin to the tolerance of numerical solvers - focusing instead on point-wise comparisons between their solution and the ones obtained by a solver on a set of inputs. In real-world applications, one cannot consider tests on a finite set of points to be sufficient grounds for deployment, as the performance could be substantially worse on a different set. To alleviate this issue, we establish tolerance-based correctness conditions for PINNs over the entire input domain. To verify the extent to which they hold, we introduce $\partial$-CROWN: a general, efficient and scalable post-training framework to bound PINN residual errors. We demonstrate its effectiveness in obtaining tight certificates by applying it to two classically studied PDEs - Burgers' and Schr\"odinger's equations -, and two more challenging ones with real-world applications - the Allan-Cahn and Diffusion-Sorption equations.

Lookback for Learning to Branch

The expressive and computationally inexpensive bipartite Graph Neural Networks (GNN) have been shown to be an important component of deep learning based Mixed-Integer Linear Program (MILP) solvers. Recent works have demonstrated the effectiveness of such GNNs in replacing the branching (variable selection) heuristic in branch-and-bound (B&B) solvers. These GNNs are trained, offline and on a collection of MILPs, to imitate a very good but computationally expensive branching heuristic, strong branching. Given that B&B results in a tree of sub-MILPs, we ask (a) whether there are strong dependencies exhibited by the target heuristic among the neighboring nodes of the B&B tree, and (b) if so, whether we can incorporate them in our training procedure. Specifically, we find that with the strong branching heuristic, a child node's best choice was often the parent's second-best choice. We call this the "lookback" phenomenon. Surprisingly, the typical branching GNN of Gasse et al. (2019) often misses this simple "answer". To imitate the target behavior more closely by incorporating the lookback phenomenon in GNNs, we propose two methods: (a) target smoothing for the standard cross-entropy loss function, and (b) adding a Parent-as-Target (PAT) Lookback regularizer term. Finally, we propose a model selection framework to incorporate harder-to-formulate objectives such as solving time in the final models. Through extensive experimentation on standard benchmark instances, we show that our proposal results in up to 22% decrease in the size of the B&B tree and up to 15% improvement in the solving times.

IBP Regularization for Verified Adversarial Robustness via Branch-and-Bound

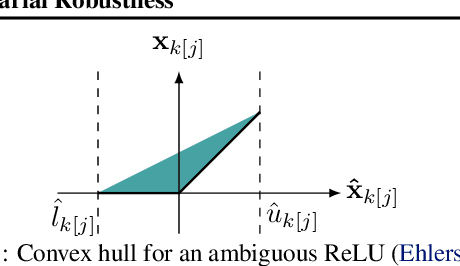
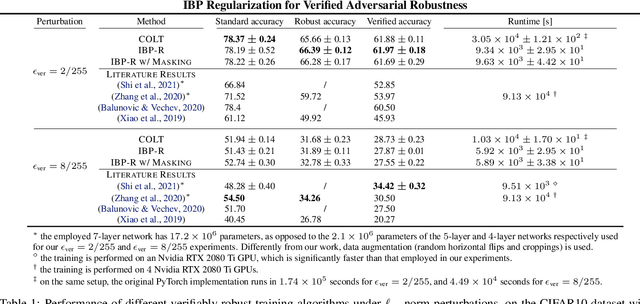
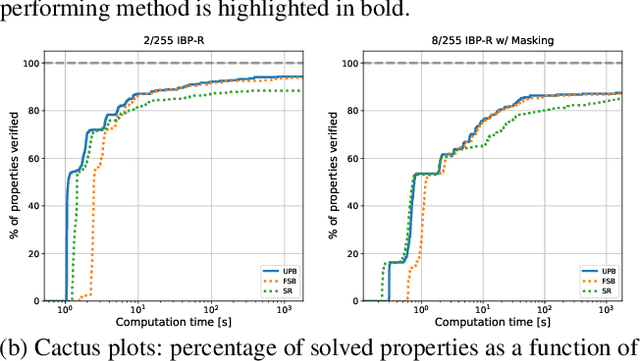
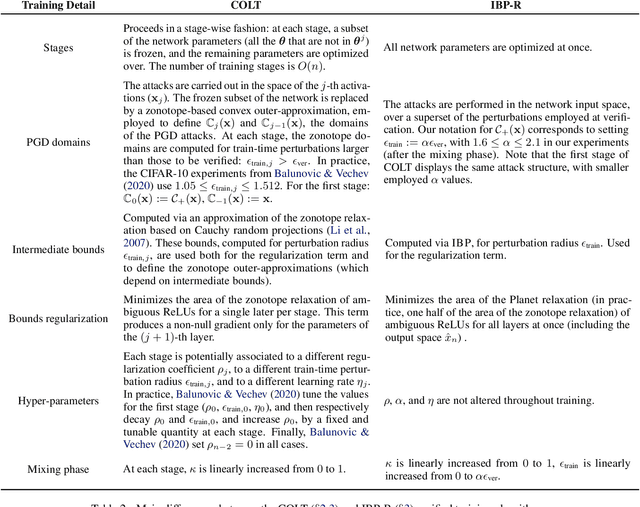
Recent works have tried to increase the verifiability of adversarially trained networks by running the attacks over domains larger than the original perturbations and adding various regularization terms to the objective. However, these algorithms either underperform or require complex and expensive stage-wise training procedures, hindering their practical applicability. We present IBP-R, a novel verified training algorithm that is both simple and effective. IBP-R induces network verifiability by coupling adversarial attacks on enlarged domains with a regularization term, based on inexpensive interval bound propagation, that minimizes the gap between the non-convex verification problem and its approximations. By leveraging recent branch-and-bound frameworks, we show that IBP-R obtains state-of-the-art verified robustness-accuracy trade-offs for small perturbations on CIFAR-10 while training significantly faster than relevant previous work. Additionally, we present UPB, a novel branching strategy that, relying on a simple heuristic based on $\beta$-CROWN, reduces the cost of state-of-the-art branching algorithms while yielding splits of comparable quality.

A Stochastic Bundle Method for Interpolating Networks

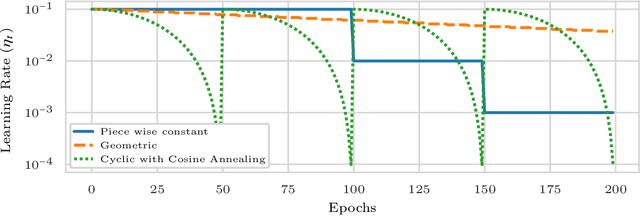
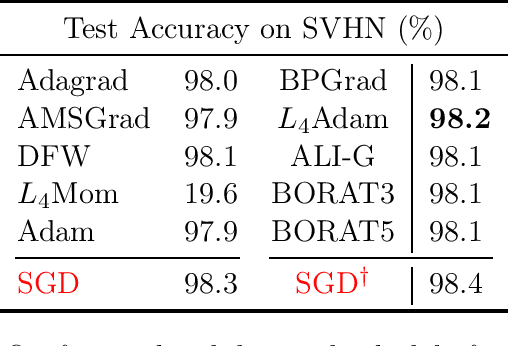
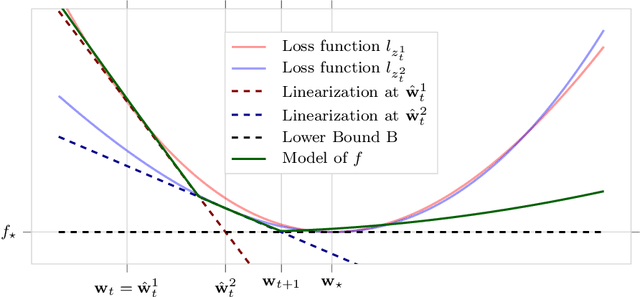
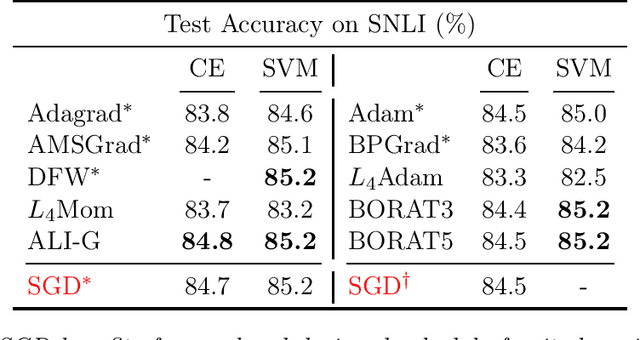
We propose a novel method for training deep neural networks that are capable of interpolation, that is, driving the empirical loss to zero. At each iteration, our method constructs a stochastic approximation of the learning objective. The approximation, known as a bundle, is a pointwise maximum of linear functions. Our bundle contains a constant function that lower bounds the empirical loss. This enables us to compute an automatic adaptive learning rate, thereby providing an accurate solution. In addition, our bundle includes linear approximations computed at the current iterate and other linear estimates of the DNN parameters. The use of these additional approximations makes our method significantly more robust to its hyperparameters. Based on its desirable empirical properties, we term our method Bundle Optimisation for Robust and Accurate Training (BORAT). In order to operationalise BORAT, we design a novel algorithm for optimising the bundle approximation efficiently at each iteration. We establish the theoretical convergence of BORAT in both convex and non-convex settings. Using standard publicly available data sets, we provide a thorough comparison of BORAT to other single hyperparameter optimisation algorithms. Our experiments demonstrate BORAT matches the state-of-the-art generalisation performance for these methods and is the most robust.

In Defense of the Unitary Scalarization for Deep Multi-Task Learning

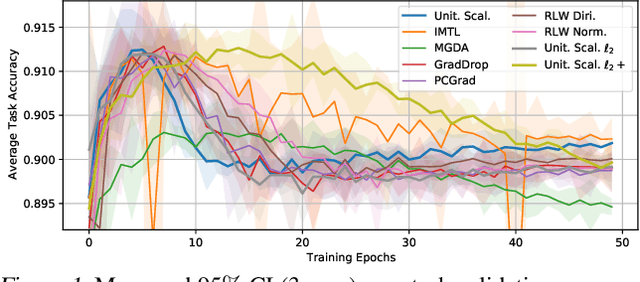
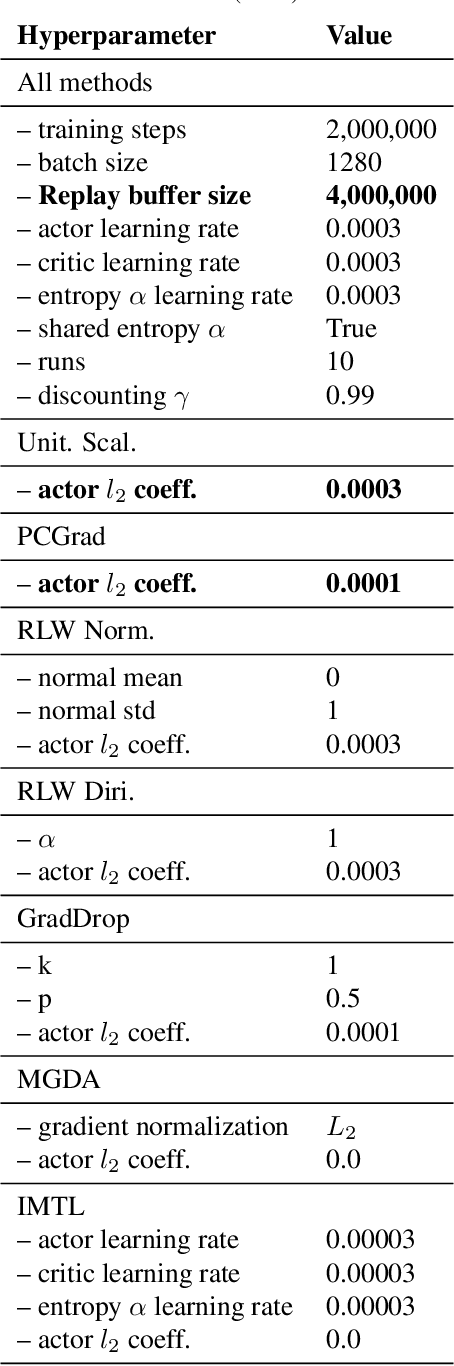
Recent multi-task learning research argues against unitary scalarization, where training simply minimizes the sum of the task losses. Several ad-hoc multi-task optimization algorithms have instead been proposed, inspired by various hypotheses about what makes multi-task settings difficult. The majority of these optimizers require per-task gradients, and introduce significant memory, runtime, and implementation overhead. We present a theoretical analysis suggesting that many specialized multi-task optimizers can be interpreted as forms of regularization. Moreover, we show that, when coupled with standard regularization and stabilization techniques from single-task learning, unitary scalarization matches or improves upon the performance of complex multi-task optimizers in both supervised and reinforcement learning settings. We believe our results call for a critical reevaluation of recent research in the area.

Learning to be adversarially robust and differentially private

We study the difficulties in learning that arise from robust and differentially private optimization. We first study convergence of gradient descent based adversarial training with differential privacy, taking a simple binary classification task on linearly separable data as an illustrative example. We compare the gap between adversarial and nominal risk in both private and non-private settings, showing that the data dimensionality dependent term introduced by private optimization compounds the difficulties of learning a robust model. After this, we discuss what parts of adversarial training and differential privacy hurt optimization, identifying that the size of adversarial perturbation and clipping norm in differential privacy both increase the curvature of the loss landscape, implying poorer generalization performance.