AlphaEvolve: A coding agent for scientific and algorithmic discovery

In this white paper, we present AlphaEvolve, an evolutionary coding agent that substantially enhances capabilities of state-of-the-art LLMs on highly challenging tasks such as tackling open scientific problems or optimizing critical pieces of computational infrastructure. AlphaEvolve orchestrates an autonomous pipeline of LLMs, whose task is to improve an algorithm by making direct changes to the code. Using an evolutionary approach, continuously receiving feedback from one or more evaluators, AlphaEvolve iteratively improves the algorithm, potentially leading to new scientific and practical discoveries. We demonstrate the broad applicability of this approach by applying it to a number of important computational problems. When applied to optimizing critical components of large-scale computational stacks at Google, AlphaEvolve developed a more efficient scheduling algorithm for data centers, found a functionally equivalent simplification in the circuit design of hardware accelerators, and accelerated the training of the LLM underpinning AlphaEvolve itself. Furthermore, AlphaEvolve discovered novel, provably correct algorithms that surpass state-of-the-art solutions on a spectrum of problems in mathematics and computer science, significantly expanding the scope of prior automated discovery methods (Romera-Paredes et al., 2023). Notably, AlphaEvolve developed a search algorithm that found a procedure to multiply two $4 \times 4$ complex-valued matrices using $48$ scalar multiplications; offering the first improvement, after 56 years, over Strassen's algorithm in this setting. We believe AlphaEvolve and coding agents like it can have a significant impact in improving solutions of problems across many areas of science and computation.

Graph Neural Networks for Link Prediction with Subgraph Sketching

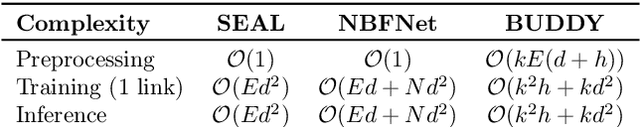
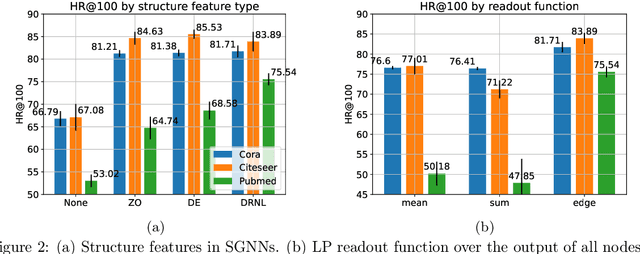
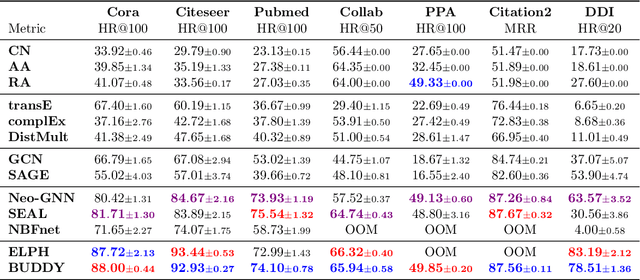
Many Graph Neural Networks (GNNs) perform poorly compared to simple heuristics on Link Prediction (LP) tasks. This is due to limitations in expressive power such as the inability to count triangles (the backbone of most LP heuristics) and because they can not distinguish automorphic nodes (those having identical structural roles). Both expressiveness issues can be alleviated by learning link (rather than node) representations and incorporating structural features such as triangle counts. Since explicit link representations are often prohibitively expensive, recent works resorted to subgraph-based methods, which have achieved state-of-the-art performance for LP, but suffer from poor efficiency due to high levels of redundancy between subgraphs. We analyze the components of subgraph GNN (SGNN) methods for link prediction. Based on our analysis, we propose a novel full-graph GNN called ELPH (Efficient Link Prediction with Hashing) that passes subgraph sketches as messages to approximate the key components of SGNNs without explicit subgraph construction. ELPH is provably more expressive than Message Passing GNNs (MPNNs). It outperforms existing SGNN models on many standard LP benchmarks while being orders of magnitude faster. However, it shares the common GNN limitation that it is only efficient when the dataset fits in GPU memory. Accordingly, we develop a highly scalable model, called BUDDY, which uses feature precomputation to circumvent this limitation without sacrificing predictive performance. Our experiments show that BUDDY also outperforms SGNNs on standard LP benchmarks while being highly scalable and faster than ELPH.

Differentiating the Black-Box: Optimization with Local Generative Surrogates

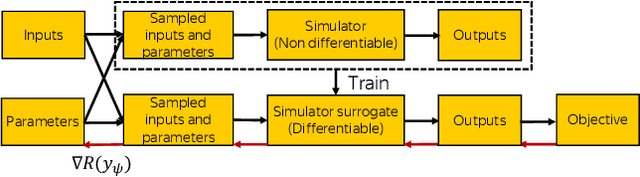
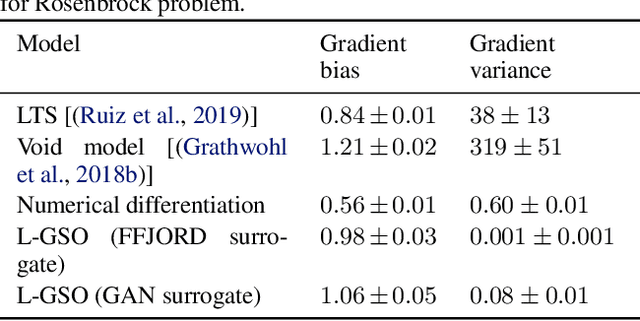
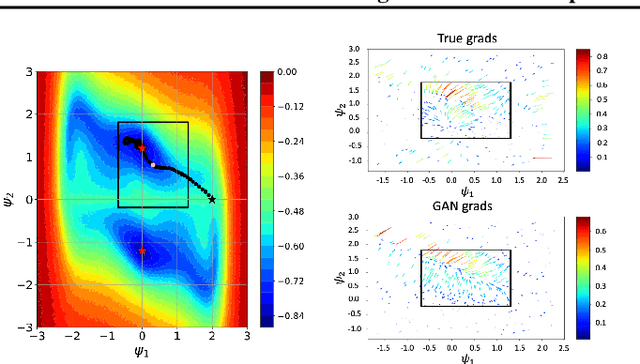
We propose a novel method for gradient-based optimization of black-box simulators using differentiable local surrogate models. In fields such as physics and engineering, many processes are modeled with non-differentiable simulators with intractable likelihoods. Optimization of these forward models is particularly challenging, especially when the simulator is stochastic. To address such cases, we introduce the use of deep generative models to iteratively approximate the simulator in local neighborhoods of the parameter space. We demonstrate that these local surrogates can be used to approximate the gradient of the simulator, and thus enable gradient-based optimization of simulator parameters. In cases where the dependence of the simulator on the parameter space is constrained to a low dimensional submanifold, we observe that our method attains minima faster than all baseline methods, including Bayesian optimization, numerical optimization, and REINFORCE driven approaches.