Gaussian Processes for Probabilistic Estimates of Earthquake Ground Shaking: A 1-D Proof-of-Concept

Estimates of seismic wave speeds in the Earth (seismic velocity models) are key input parameters to earthquake simulations for ground motion prediction. Owing to the non-uniqueness of the seismic inverse problem, typically many velocity models exist for any given region. The arbitrary choice of which velocity model to use in earthquake simulations impacts ground motion predictions. However, current hazard analysis methods do not account for this source of uncertainty. We present a proof-of-concept ground motion prediction workflow for incorporating uncertainties arising from inconsistencies between existing seismic velocity models. Our analysis is based on the probabilistic fusion of overlapping seismic velocity models using scalable Gaussian process (GP) regression. Specifically, we fit a GP to two synthetic 1-D velocity profiles simultaneously, and show that the predictive uncertainty accounts for the differences between the models. We subsequently draw velocity model samples from the predictive distribution and estimate peak ground displacement using acoustic wave propagation through the velocity models. The resulting distribution of possible ground motion amplitudes is much wider than would be predicted by simulating shaking using only the two input velocity models. This proof-of-concept illustrates the importance of probabilistic methods for physics-based seismic hazard analysis.

A Foundation Model for the Solar Dynamics Observatory

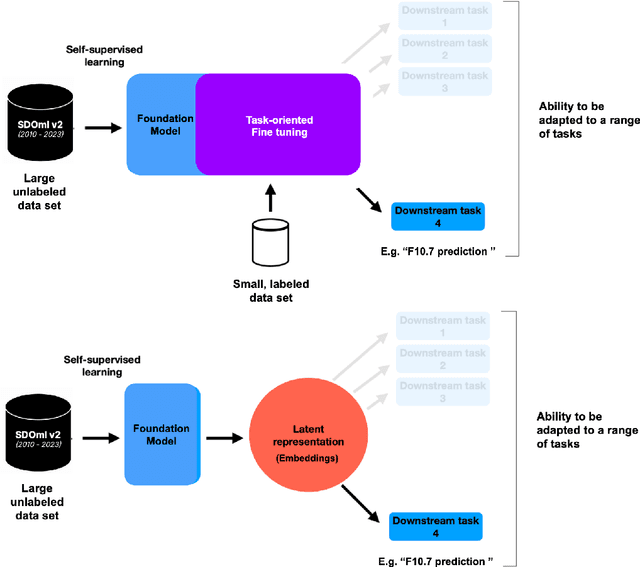
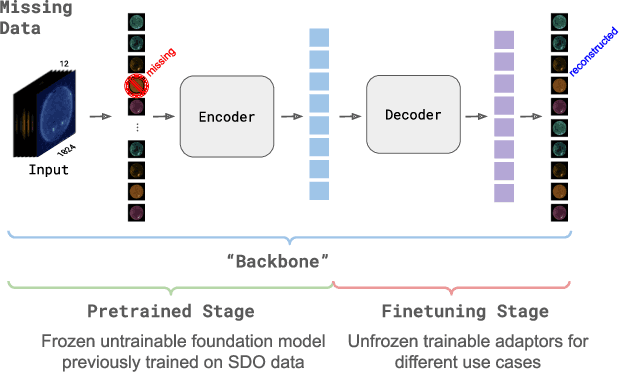
SDO-FM is a foundation model using data from NASA's Solar Dynamics Observatory (SDO) spacecraft; integrating three separate instruments to encapsulate the Sun's complex physical interactions into a multi-modal embedding space. This model can be used to streamline scientific investigations involving SDO by making the enormous datasets more computationally accessible for heliophysics research and enable investigations that require instrument fusion. We discuss four key components: an ingestion pipeline to create machine learning ready datasets, the model architecture and training approach, resultant embeddings and fine-tunable models, and finally downstream fine-tuned applications. A key component of this effort has been to include subject matter specialists at each stage of development; reviewing the scientific value and providing guidance for model architecture, dataset, and training paradigm decisions. This paper marks release of our pretrained models and embedding datasets, available to the community on Hugging Face and sdofm.org.

Second-Order Forward-Mode Automatic Differentiation for Optimization

This paper introduces a second-order hyperplane search, a novel optimization step that generalizes a second-order line search from a line to a $k$-dimensional hyperplane. This, combined with the forward-mode stochastic gradient method, yields a second-order optimization algorithm that consists of forward passes only, completely avoiding the storage overhead of backpropagation. Unlike recent work that relies on directional derivatives (or Jacobian--Vector Products, JVPs), we use hyper-dual numbers to jointly evaluate both directional derivatives and their second-order quadratic terms. As a result, we introduce forward-mode weight perturbation with Hessian information (FoMoH). We then use FoMoH to develop a novel generalization of line search by extending it to a hyperplane search. We illustrate the utility of this extension and how it might be used to overcome some of the recent challenges of optimizing machine learning models without backpropagation. Our code is open-sourced at https://github.com/SRI-CSL/fomoh.

Closing the Gap Between SGP4 and High-Precision Propagation via Differentiable Programming

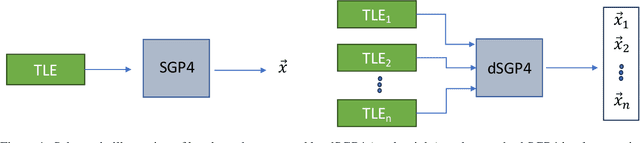
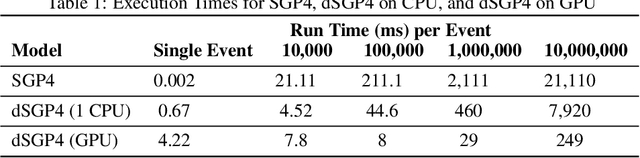
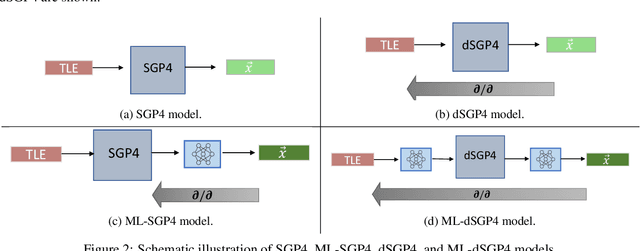
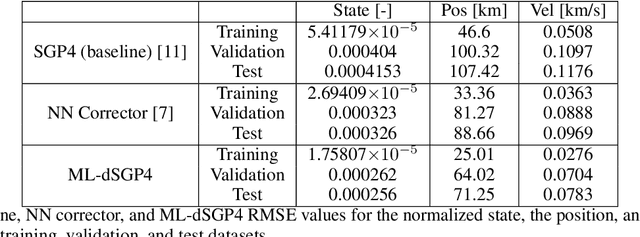
The Simplified General Perturbations 4 (SGP4) orbital propagation method is widely used for predicting the positions and velocities of Earth-orbiting objects rapidly and reliably. Despite continuous refinement, SGP models still lack the precision of numerical propagators, which offer significantly smaller errors. This study presents dSGP4, a novel differentiable version of SGP4 implemented using PyTorch. By making SGP4 differentiable, dSGP4 facilitates various space-related applications, including spacecraft orbit determination, state conversion, covariance transformation, state transition matrix computation, and covariance propagation. Additionally, dSGP4's PyTorch implementation allows for embarrassingly parallel orbital propagation across batches of Two-Line Element Sets (TLEs), leveraging the computational power of CPUs, GPUs, and advanced hardware for distributed prediction of satellite positions at future times. Furthermore, dSGP4's differentiability enables integration with modern machine learning techniques. Thus, we propose a novel orbital propagation paradigm, ML-dSGP4, where neural networks are integrated into the orbital propagator. Through stochastic gradient descent, this combined model's inputs, outputs, and parameters can be iteratively refined, surpassing SGP4's precision. Neural networks act as identity operators by default, adhering to SGP4's behavior. However, dSGP4's differentiability allows fine-tuning with ephemeris data, enhancing precision while maintaining computational speed. This empowers satellite operators and researchers to train the model using specific ephemeris or high-precision numerical propagation data, significantly advancing orbital prediction capabilities.

Managing AI Risks in an Era of Rapid Progress

In this short consensus paper, we outline risks from upcoming, advanced AI systems. We examine large-scale social harms and malicious uses, as well as an irreversible loss of human control over autonomous AI systems. In light of rapid and continuing AI progress, we propose priorities for AI R&D and governance.

Gradients without Backpropagation

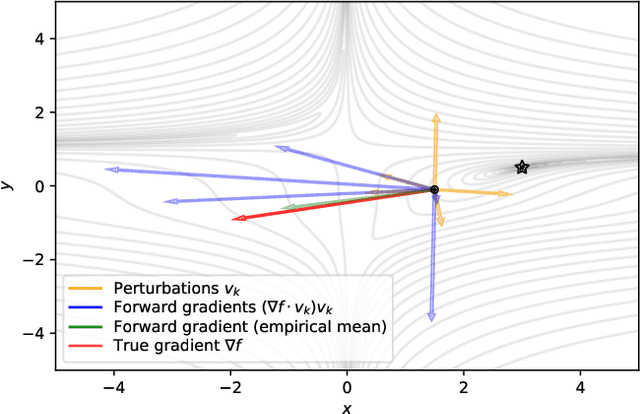
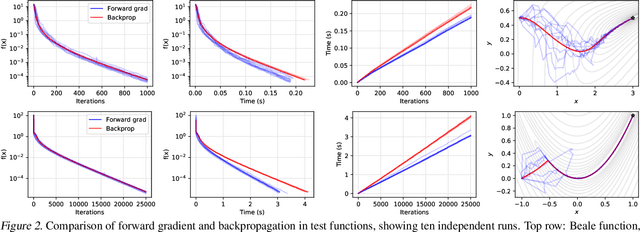
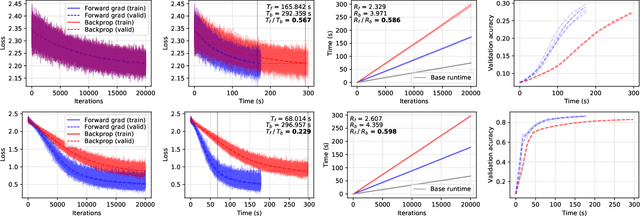
Using backpropagation to compute gradients of objective functions for optimization has remained a mainstay of machine learning. Backpropagation, or reverse-mode differentiation, is a special case within the general family of automatic differentiation algorithms that also includes the forward mode. We present a method to compute gradients based solely on the directional derivative that one can compute exactly and efficiently via the forward mode. We call this formulation the forward gradient, an unbiased estimate of the gradient that can be evaluated in a single forward run of the function, entirely eliminating the need for backpropagation in gradient descent. We demonstrate forward gradient descent in a range of problems, showing substantial savings in computation and enabling training up to twice as fast in some cases.

Simultaneous Multivariate Forecast of Space Weather Indices using Deep Neural Network Ensembles

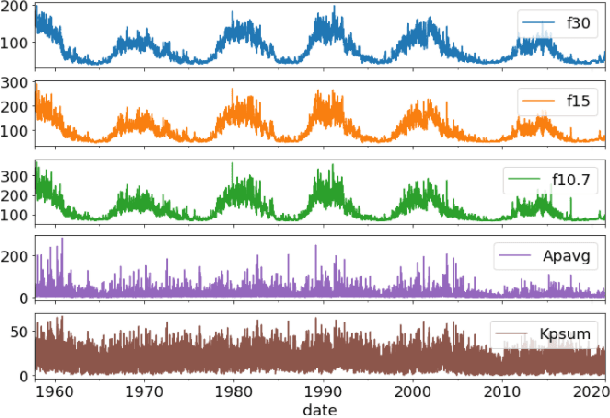
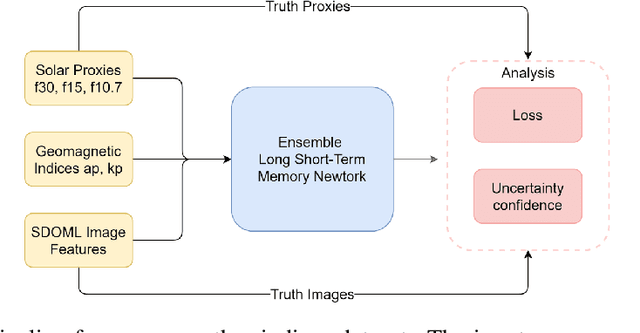
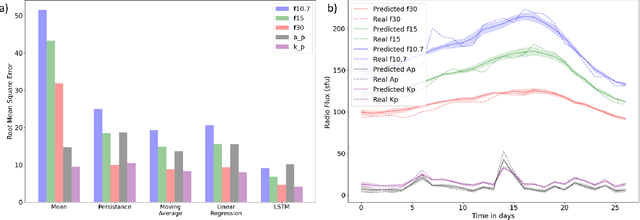
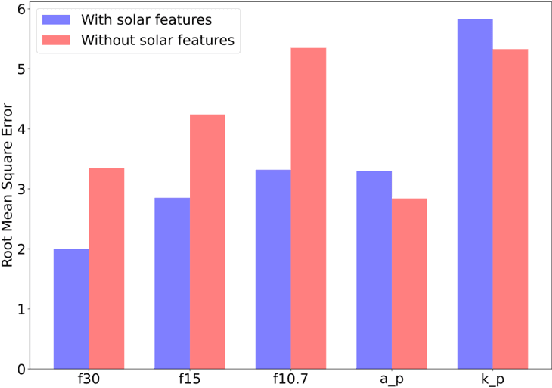
Solar radio flux along with geomagnetic indices are important indicators of solar activity and its effects. Extreme solar events such as flares and geomagnetic storms can negatively affect the space environment including satellites in low-Earth orbit. Therefore, forecasting these space weather indices is of great importance in space operations and science. In this study, we propose a model based on long short-term memory neural networks to learn the distribution of time series data with the capability to provide a simultaneous multivariate 27-day forecast of the space weather indices using time series as well as solar image data. We show a 30-40\% improvement of the root mean-square error while including solar image data with time series data compared to using time series data alone. Simple baselines such as a persistence and running average forecasts are also compared with the trained deep neural network models. We also quantify the uncertainty in our prediction using a model ensemble.

Simulation Intelligence: Towards a New Generation of Scientific Methods

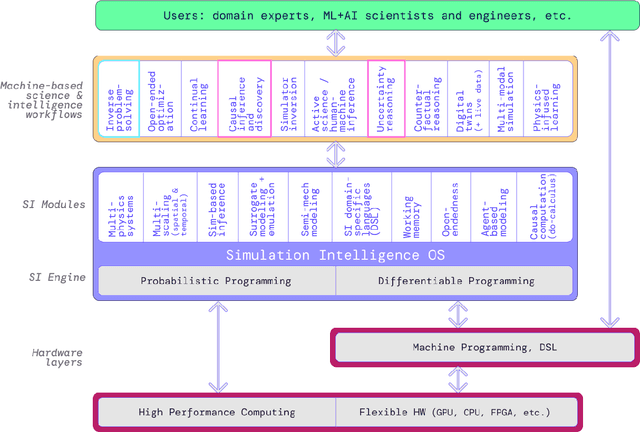
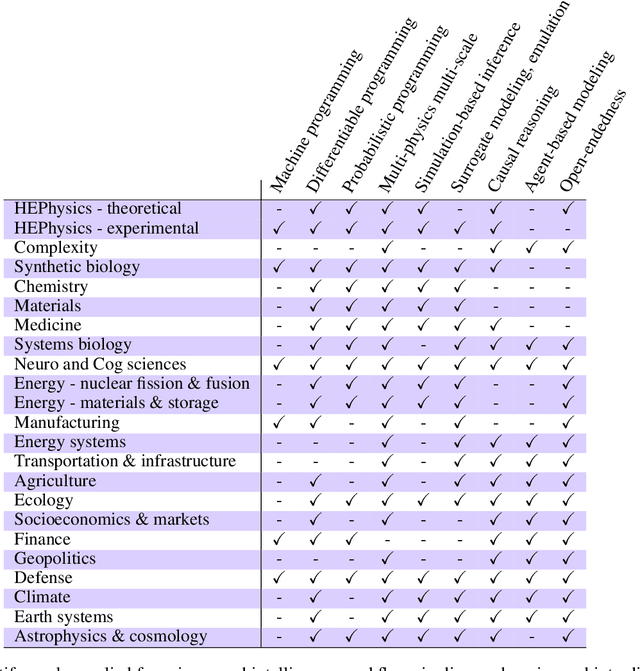
The original "Seven Motifs" set forth a roadmap of essential methods for the field of scientific computing, where a motif is an algorithmic method that captures a pattern of computation and data movement. We present the "Nine Motifs of Simulation Intelligence", a roadmap for the development and integration of the essential algorithms necessary for a merger of scientific computing, scientific simulation, and artificial intelligence. We call this merger simulation intelligence (SI), for short. We argue the motifs of simulation intelligence are interconnected and interdependent, much like the components within the layers of an operating system. Using this metaphor, we explore the nature of each layer of the simulation intelligence operating system stack (SI-stack) and the motifs therein: (1) Multi-physics and multi-scale modeling; (2) Surrogate modeling and emulation; (3) Simulation-based inference; (4) Causal modeling and inference; (5) Agent-based modeling; (6) Probabilistic programming; (7) Differentiable programming; (8) Open-ended optimization; (9) Machine programming. We believe coordinated efforts between motifs offers immense opportunity to accelerate scientific discovery, from solving inverse problems in synthetic biology and climate science, to directing nuclear energy experiments and predicting emergent behavior in socioeconomic settings. We elaborate on each layer of the SI-stack, detailing the state-of-art methods, presenting examples to highlight challenges and opportunities, and advocating for specific ways to advance the motifs and the synergies from their combinations. Advancing and integrating these technologies can enable a robust and efficient hypothesis-simulation-analysis type of scientific method, which we introduce with several use-cases for human-machine teaming and automated science.

Detecting and Quantifying Malicious Activity with Simulation-based Inference

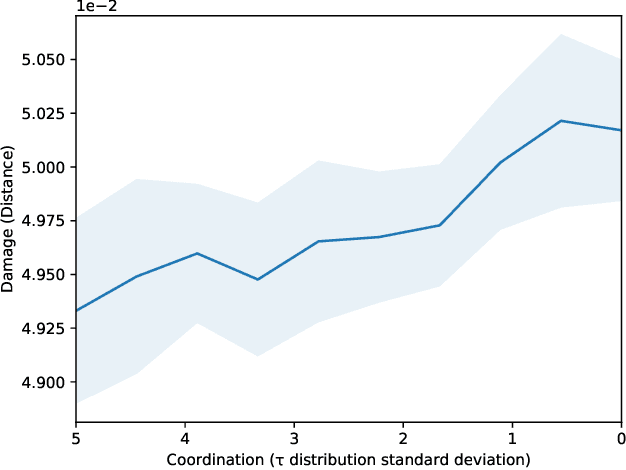
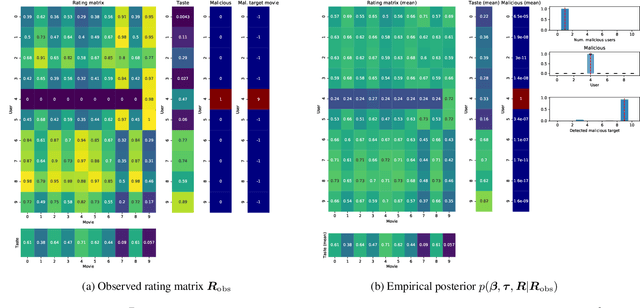
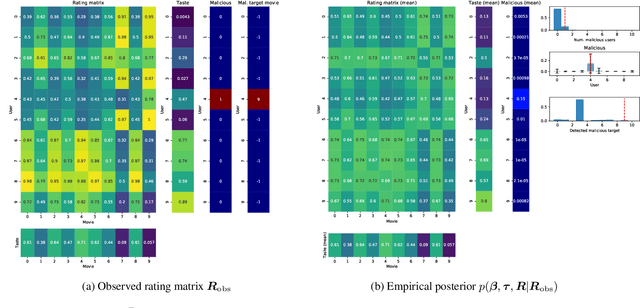
We propose the use of probabilistic programming techniques to tackle the malicious user identification problem in a recommendation algorithm. Probabilistic programming provides numerous advantages over other techniques, including but not limited to providing a disentangled representation of how malicious users acted under a structured model, as well as allowing for the quantification of damage caused by malicious users. We show experiments in malicious user identification using a model of regular and malicious users interacting with a simple recommendation algorithm, and provide a novel simulation-based measure for quantifying the effects of a user or group of users on its dynamics.

KL Guided Domain Adaptation

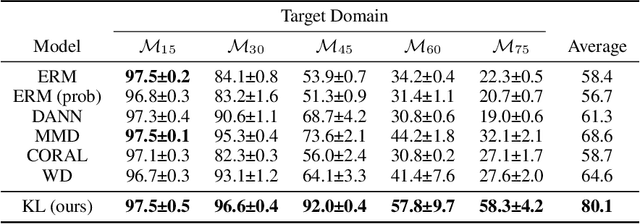
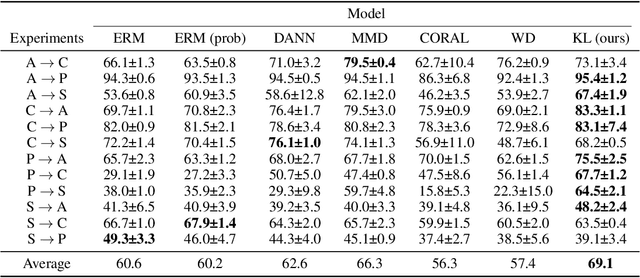
Domain adaptation is an important problem and often needed for real-world applications. In this problem, instead of i.i.d. datapoints, we assume that the source (training) data and the target (testing) data have different distributions. With that setting, the empirical risk minimization training procedure often does not perform well, since it does not account for the change in the distribution. A common approach in the domain adaptation literature is to learn a representation of the input that has the same distributions over the source and the target domain. However, these approaches often require additional networks and/or optimizing an adversarial (minimax) objective, which can be very expensive or unstable in practice. To tackle this problem, we first derive a generalization bound for the target loss based on the training loss and the reverse Kullback-Leibler (KL) divergence between the source and the target representation distributions. Based on this bound, we derive an algorithm that minimizes the KL term to obtain a better generalization to the target domain. We show that with a probabilistic representation network, the KL term can be estimated efficiently via minibatch samples without any additional network or a minimax objective. This leads to a theoretically sound alignment method which is also very efficient and stable in practice. Experimental results also suggest that our method outperforms other representation-alignment approaches.