FormulaOne: Measuring the Depth of Algorithmic Reasoning Beyond Competitive Programming

Frontier AI models demonstrate formidable breadth of knowledge. But how close are they to true human -- or superhuman -- expertise? Genuine experts can tackle the hardest problems and push the boundaries of scientific understanding. To illuminate the limits of frontier model capabilities, we turn away from contrived competitive programming puzzles, and instead focus on real-life research problems. We construct FormulaOne, a benchmark that lies at the intersection of graph theory, logic, and algorithms, all well within the training distribution of frontier models. Our problems are incredibly demanding, requiring an array of reasoning steps. The dataset has three key properties. First, it is of commercial interest and relates to practical large-scale optimisation problems, such as those arising in routing, scheduling, and network design. Second, it is generated from the highly expressive framework of Monadic Second-Order (MSO) logic on graphs, paving the way toward automatic problem generation at scale; ideal for building RL environments. Third, many of our problems are intimately related to the frontier of theoretical computer science, and to central conjectures therein, such as the Strong Exponential Time Hypothesis (SETH). As such, any significant algorithmic progress on our dataset, beyond known results, could carry profound theoretical implications. Remarkably, state-of-the-art models like OpenAI's o3 fail entirely on FormulaOne, solving less than 1% of the questions, even when given 10 attempts and explanatory fewshot examples -- highlighting how far they remain from expert-level understanding in some domains. To support further research, we additionally curate FormulaOne-Warmup, offering a set of simpler tasks, from the same distribution. We release the full corpus along with a comprehensive evaluation framework.

Artificial Expert Intelligence through PAC-reasoning

Artificial Expert Intelligence (AEI) seeks to transcend the limitations of both Artificial General Intelligence (AGI) and narrow AI by integrating domain-specific expertise with critical, precise reasoning capabilities akin to those of top human experts. Existing AI systems often excel at predefined tasks but struggle with adaptability and precision in novel problem-solving. To overcome this, AEI introduces a framework for ``Probably Approximately Correct (PAC) Reasoning". This paradigm provides robust theoretical guarantees for reliably decomposing complex problems, with a practical mechanism for controlling reasoning precision. In reference to the division of human thought into System 1 for intuitive thinking and System 2 for reflective reasoning~\citep{tversky1974judgment}, we refer to this new type of reasoning as System 3 for precise reasoning, inspired by the rigor of the scientific method. AEI thus establishes a foundation for error-bounded, inference-time learning.

Untangling Lariats: Subgradient Following of Variationally Penalized Objectives

We describe a novel subgradient following apparatus for calculating the optimum of convex problems with variational penalties. In this setting, we receive a sequence $y_i,\ldots,y_n$ and seek a smooth sequence $x_1,\ldots,x_n$. The smooth sequence attains the minimum Bregman divergence to an input sequence with additive variational penalties in the general form of $\sum_i g_i(x_{i+1}-x_i)$. We derive, as special cases of our apparatus, known algorithms for the fused lasso and isotonic regression. Our approach also facilitates new variational penalties such as non-smooth barrier functions. We next derive and analyze multivariate problems in which $\mathbf{x}_i,\mathbf{y}_i\in\mathbb{R}^d$ and variational penalties that depend on $\|\mathbf{x}_{i+1}-\mathbf{x}_i\|$. The norms we consider are $\ell_2$ and $\ell_\infty$ which promote group sparsity. Last but not least, we derive a lattice-based subgradient following for variational penalties characterized through the output of arbitrary convolutional filters. This paradigm yields efficient solvers for problems in which sparse high-order discrete derivatives such as acceleration and jerk are desirable.

Jamba: A Hybrid Transformer-Mamba Language Model

We present Jamba, a new base large language model based on a novel hybrid Transformer-Mamba mixture-of-experts (MoE) architecture. Specifically, Jamba interleaves blocks of Transformer and Mamba layers, enjoying the benefits of both model families. MoE is added in some of these layers to increase model capacity while keeping active parameter usage manageable. This flexible architecture allows resource- and objective-specific configurations. In the particular configuration we have implemented, we end up with a powerful model that fits in a single 80GB GPU. Built at large scale, Jamba provides high throughput and small memory footprint compared to vanilla Transformers, and at the same time state-of-the-art performance on standard language model benchmarks and long-context evaluations. Remarkably, the model presents strong results for up to 256K tokens context length. We study various architectural decisions, such as how to combine Transformer and Mamba layers, and how to mix experts, and show that some of them are crucial in large scale modeling. We also describe several interesting properties of these architectures which the training and evaluation of Jamba have revealed, and plan to release checkpoints from various ablation runs, to encourage further exploration of this novel architecture. We make the weights of our implementation of Jamba publicly available under a permissive license.

Managing AI Risks in an Era of Rapid Progress

In this short consensus paper, we outline risks from upcoming, advanced AI systems. We examine large-scale social harms and malicious uses, as well as an irreversible loss of human control over autonomous AI systems. In light of rapid and continuing AI progress, we propose priorities for AI R&D and governance.

SubTuning: Efficient Finetuning for Multi-Task Learning

Finetuning a pretrained model has become a standard approach for training neural networks on novel tasks, resulting in fast convergence and improved performance. In this work, we study an alternative finetuning method, where instead of finetuning all the weights of the network, we only train a carefully chosen subset of layers, keeping the rest of the weights frozen at their initial (pretrained) values. We demonstrate that \emph{subset finetuning} (or SubTuning) often achieves accuracy comparable to full finetuning of the model, and even surpasses the performance of full finetuning when training data is scarce. Therefore, SubTuning allows deploying new tasks at minimal computational cost, while enjoying the benefits of finetuning the entire model. This yields a simple and effective method for multi-task learning, where different tasks do not interfere with one another, and yet share most of the resources at inference time. We demonstrate the efficiency of SubTuning across multiple tasks, using different network architectures and pretraining methods.

MRKL Systems: A modular, neuro-symbolic architecture that combines large language models, external knowledge sources and discrete reasoning

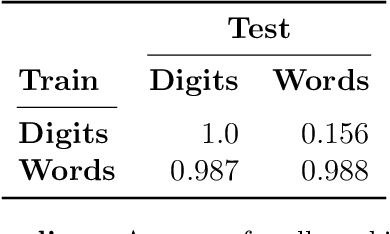
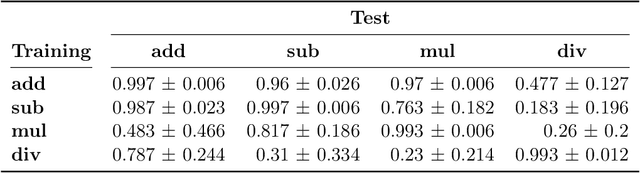
Huge language models (LMs) have ushered in a new era for AI, serving as a gateway to natural-language-based knowledge tasks. Although an essential element of modern AI, LMs are also inherently limited in a number of ways. We discuss these limitations and how they can be avoided by adopting a systems approach. Conceptualizing the challenge as one that involves knowledge and reasoning in addition to linguistic processing, we define a flexible architecture with multiple neural models, complemented by discrete knowledge and reasoning modules. We describe this neuro-symbolic architecture, dubbed the Modular Reasoning, Knowledge and Language (MRKL, pronounced "miracle") system, some of the technical challenges in implementing it, and Jurassic-X, AI21 Labs' MRKL system implementation.

Standing on the Shoulders of Giant Frozen Language Models

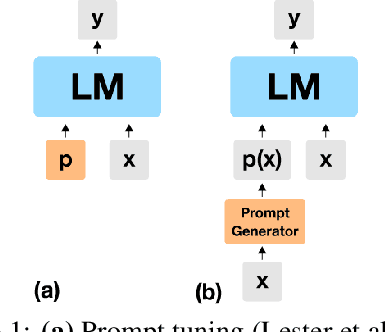
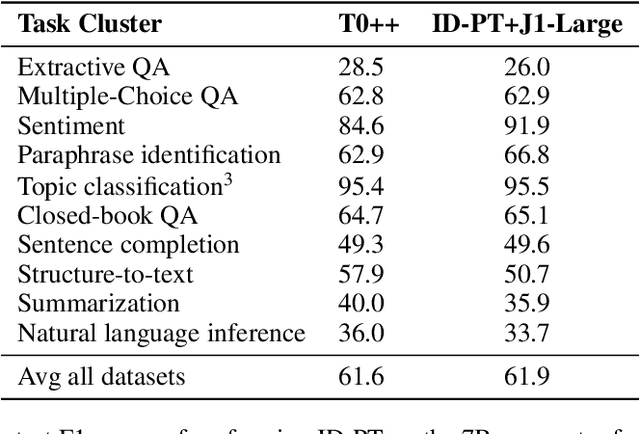
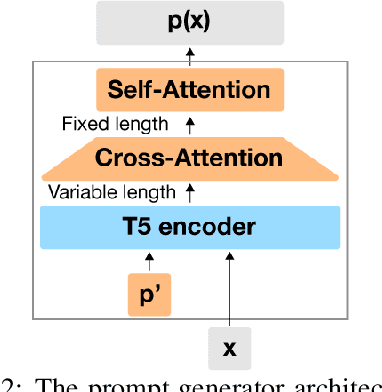
Huge pretrained language models (LMs) have demonstrated surprisingly good zero-shot capabilities on a wide variety of tasks. This gives rise to the appealing vision of a single, versatile model with a wide range of functionalities across disparate applications. However, current leading techniques for leveraging a "frozen" LM -- i.e., leaving its weights untouched -- still often underperform fine-tuning approaches which modify these weights in a task-dependent way. Those, in turn, suffer forgetfulness and compromise versatility, suggesting a tradeoff between performance and versatility. The main message of this paper is that current frozen-model techniques such as prompt tuning are only the tip of the iceberg, and more powerful methods for leveraging frozen LMs can do just as well as fine tuning in challenging domains without sacrificing the underlying model's versatility. To demonstrate this, we introduce three novel methods for leveraging frozen models: input-dependent prompt tuning, frozen readers, and recursive LMs, each of which vastly improves on current frozen-model approaches. Indeed, some of our methods even outperform fine-tuning approaches in domains currently dominated by the latter. The computational cost of each method is higher than that of existing frozen model methods, but still negligible relative to a single pass through a huge frozen LM. Each of these methods constitutes a meaningful contribution in its own right, but by presenting these contributions together we aim to convince the reader of a broader message that goes beyond the details of any given method: that frozen models have untapped potential and that fine-tuning is often unnecessary.

Knowledge Distillation: Bad Models Can Be Good Role Models

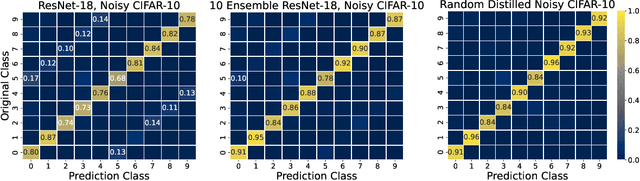
Large neural networks trained in the overparameterized regime are able to fit noise to zero train error. Recent work \citep{nakkiran2020distributional} has empirically observed that such networks behave as "conditional samplers" from the noisy distribution. That is, they replicate the noise in the train data to unseen examples. We give a theoretical framework for studying this conditional sampling behavior in the context of learning theory. We relate the notion of such samplers to knowledge distillation, where a student network imitates the outputs of a teacher on unlabeled data. We show that samplers, while being bad classifiers, can be good teachers. Concretely, we prove that distillation from samplers is guaranteed to produce a student which approximates the Bayes optimal classifier. Finally, we show that some common learning algorithms (e.g., Nearest-Neighbours and Kernel Machines) can generate samplers when applied in the overparameterized regime.

The Connection Between Approximation, Depth Separation and Learnability in Neural Networks

Several recent works have shown separation results between deep neural networks, and hypothesis classes with inferior approximation capacity such as shallow networks or kernel classes. On the other hand, the fact that deep networks can efficiently express a target function does not mean this target function can be learned efficiently by deep neural networks. In this work we study the intricate connection between learnability and approximation capacity. We show that learnability with deep networks of a target function depends on the ability of simpler classes to approximate the target. Specifically, we show that a necessary condition for a function to be learnable by gradient descent on deep neural networks is to be able to approximate the function, at least in a weak sense, with shallow neural networks. We also show that a class of functions can be learned by an efficient statistical query algorithm if and only if it can be approximated in a weak sense by some kernel class. We give several examples of functions which demonstrate depth separation, and conclude that they cannot be efficiently learned, even by a hypothesis class that can efficiently approximate them.