Ido Ben-Shaul
Artificial Expert Intelligence through PAC-reasoning
Dec 03, 2024Abstract:Artificial Expert Intelligence (AEI) seeks to transcend the limitations of both Artificial General Intelligence (AGI) and narrow AI by integrating domain-specific expertise with critical, precise reasoning capabilities akin to those of top human experts. Existing AI systems often excel at predefined tasks but struggle with adaptability and precision in novel problem-solving. To overcome this, AEI introduces a framework for ``Probably Approximately Correct (PAC) Reasoning". This paradigm provides robust theoretical guarantees for reliably decomposing complex problems, with a practical mechanism for controlling reasoning precision. In reference to the division of human thought into System 1 for intuitive thinking and System 2 for reflective reasoning~\citep{tversky1974judgment}, we refer to this new type of reasoning as System 3 for precise reasoning, inspired by the rigor of the scientific method. AEI thus establishes a foundation for error-bounded, inference-time learning.
Reverse Engineering Self-Supervised Learning
May 24, 2023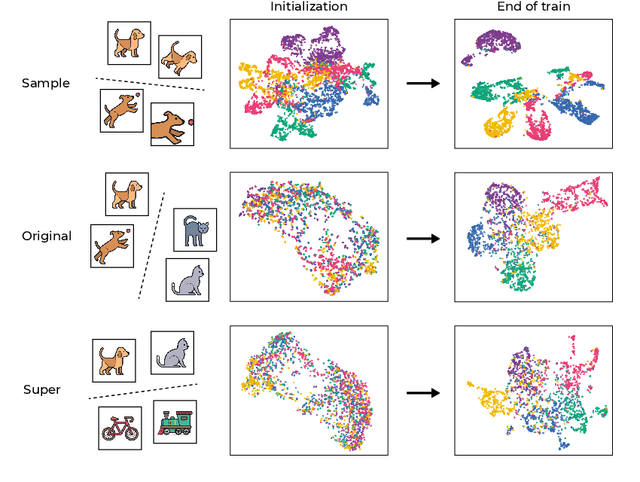
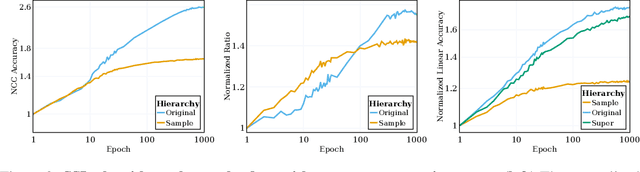
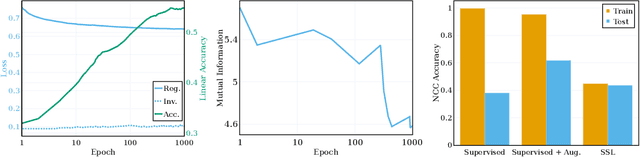
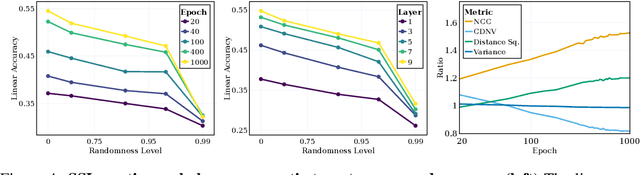
Abstract:Self-supervised learning (SSL) is a powerful tool in machine learning, but understanding the learned representations and their underlying mechanisms remains a challenge. This paper presents an in-depth empirical analysis of SSL-trained representations, encompassing diverse models, architectures, and hyperparameters. Our study reveals an intriguing aspect of the SSL training process: it inherently facilitates the clustering of samples with respect to semantic labels, which is surprisingly driven by the SSL objective's regularization term. This clustering process not only enhances downstream classification but also compresses the data information. Furthermore, we establish that SSL-trained representations align more closely with semantic classes rather than random classes. Remarkably, we show that learned representations align with semantic classes across various hierarchical levels, and this alignment increases during training and when moving deeper into the network. Our findings provide valuable insights into SSL's representation learning mechanisms and their impact on performance across different sets of classes.
Exploring the Approximation Capabilities of Multiplicative Neural Networks for Smooth Functions
Jan 11, 2023
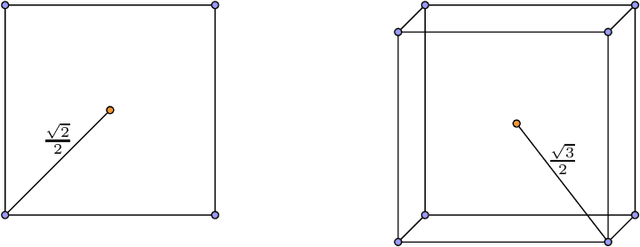
Abstract:Multiplication layers are a key component in various influential neural network modules, including self-attention and hypernetwork layers. In this paper, we investigate the approximation capabilities of deep neural networks with intermediate neurons connected by simple multiplication operations. We consider two classes of target functions: generalized bandlimited functions, which are frequently used to model real-world signals with finite bandwidth, and Sobolev-Type balls, which are embedded in the Sobolev Space $\mathcal{W}^{r,2}$. Our results demonstrate that multiplicative neural networks can approximate these functions with significantly fewer layers and neurons compared to standard ReLU neural networks, with respect to both input dimension and approximation error. These findings suggest that multiplicative gates can outperform standard feed-forward layers and have potential for improving neural network design.
Nearest Class-Center Simplification through Intermediate Layers
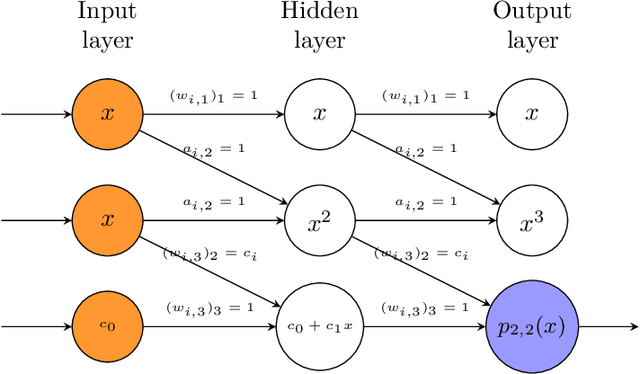
Jan 21, 2022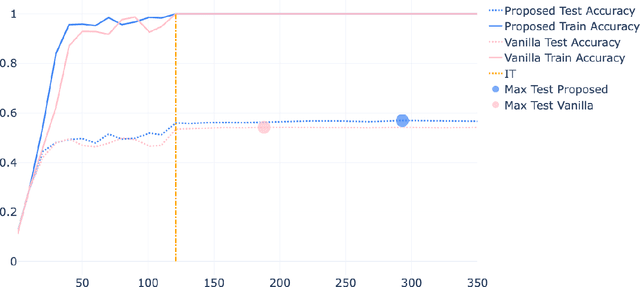
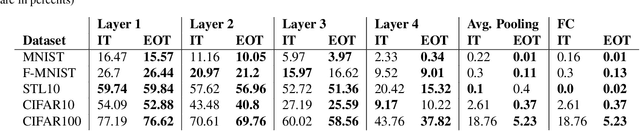
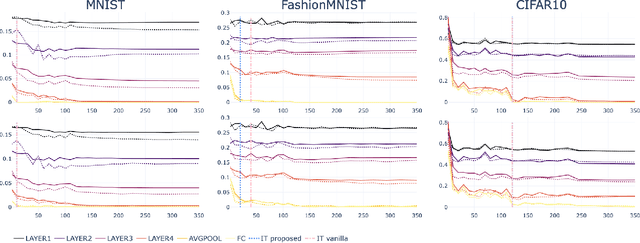
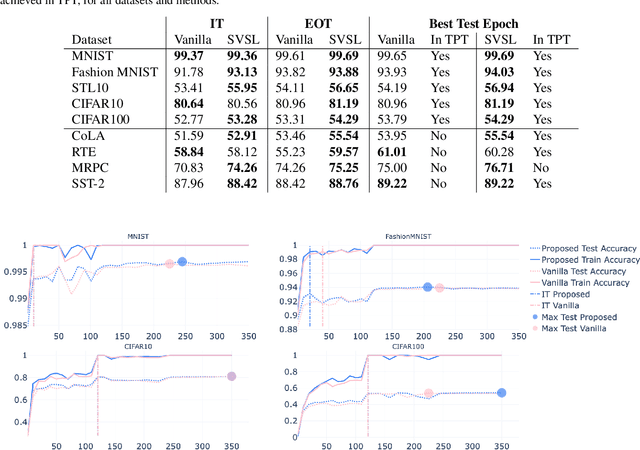
Abstract:Recent advances in theoretical Deep Learning have introduced geometric properties that occur during training, past the Interpolation Threshold -- where the training error reaches zero. We inquire into the phenomena coined Neural Collapse in the intermediate layers of the networks, and emphasize the innerworkings of Nearest Class-Center Mismatch inside the deepnet. We further show that these processes occur both in vision and language model architectures. Lastly, we propose a Stochastic Variability-Simplification Loss (SVSL) that encourages better geometrical features in intermediate layers, and improves both train metrics and generalization.
Sparsity-Probe: Analysis tool for Deep Learning Models
May 14, 2021


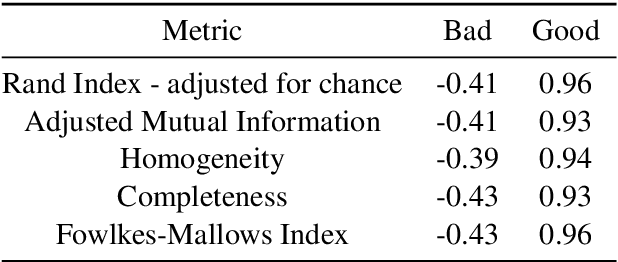
Abstract:We propose a probe for the analysis of deep learning architectures that is based on machine learning and approximation theoretical principles. Given a deep learning architecture and a training set, during or after training, the Sparsity Probe allows to analyze the performance of intermediate layers by quantifying the geometrical features of representations of the training set. We show how the Sparsity Probe enables measuring the contribution of adding depth to a given architecture, to detect under-performing layers, etc., all this without any auxiliary test data set.
Certainty Pooling for Multiple Instance Learning
Aug 24, 2020
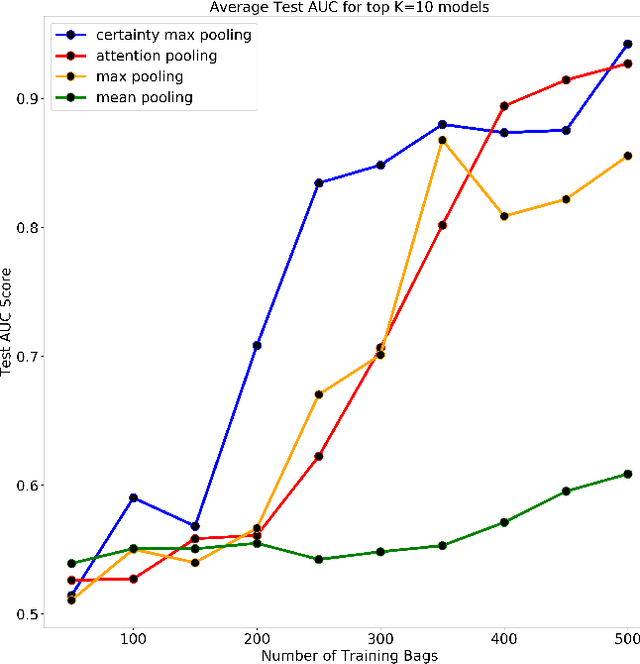


Abstract:Multiple Instance Learning is a form of weakly supervised learning in which the data is arranged in sets of instances called bags with one label assigned per bag. The bag level class prediction is derived from the multiple instances through application of a permutation invariant pooling operator on instance predictions or embeddings. We present a novel pooling operator called \textbf{Certainty Pooling} which incorporates the model certainty into bag predictions resulting in a more robust and explainable model. We compare our proposed method with other pooling operators in controlled experiments with low evidence ratio bags based on MNIST, as well as on a real life histopathology dataset - Camelyon16. Our method outperforms other methods in both bag level and instance level prediction, especially when only small training sets are available. We discuss the rationale behind our approach and the reasons for its superiority for these types of datasets.
Solving the functional Eigen-Problem using Neural Networks
Jul 20, 2020



Abstract:In this work, we explore the ability of NN (Neural Networks) to serve as a tool for finding eigen-pairs of ordinary differential equations. The question we aime to address is whether, given a self-adjoint operator, we can learn what are the eigenfunctions, and their matching eigenvalues. The topic of solving the eigen-problem is widely discussed in Image Processing, as many image processing algorithms can be thought of as such operators. We suggest an alternative to numeric methods of finding eigenpairs, which may potentially be more robust and have the ability to solve more complex problems. In this work, we focus on simple problems for which the analytical solution is known. This way, we are able to make initial steps in discovering the capabilities and shortcomings of DNN (Deep Neural Networks) in the given setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge