Wavelets Are All You Need for Autoregressive Image Generation

In this paper, we take a new approach to autoregressive image generation that is based on two main ingredients. The first is wavelet image coding, which allows to tokenize the visual details of an image from coarse to fine details by ordering the information starting with the most significant bits of the most significant wavelet coefficients. The second is a variant of a language transformer whose architecture is re-designed and optimized for token sequences in this 'wavelet language'. The transformer learns the significant statistical correlations within a token sequence, which are the manifestations of well-known correlations between the wavelet subbands at various resolutions. We show experimental results with conditioning on the generation process.

Reverse Engineering Self-Supervised Learning

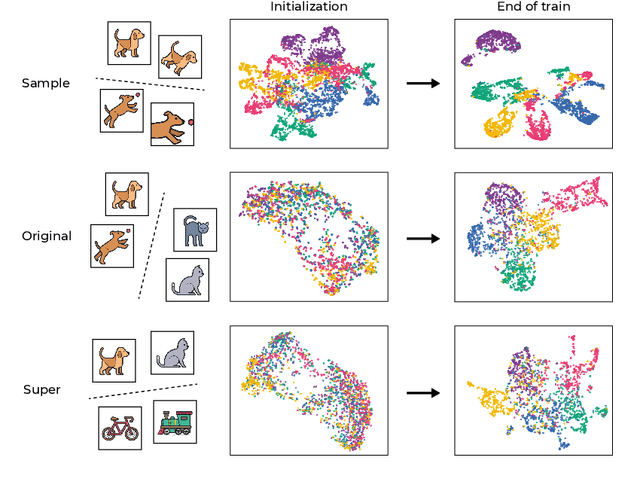
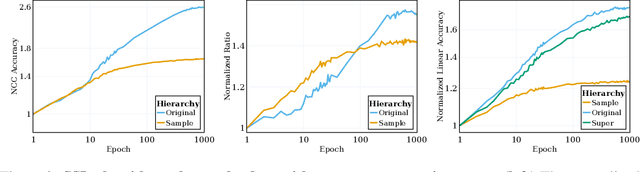
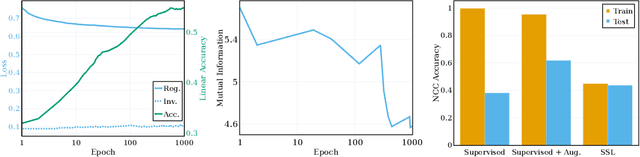
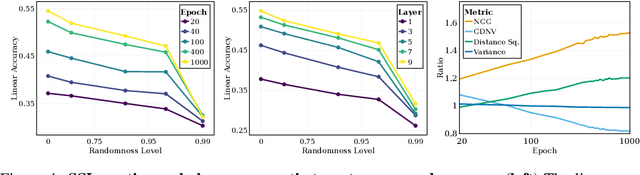
Self-supervised learning (SSL) is a powerful tool in machine learning, but understanding the learned representations and their underlying mechanisms remains a challenge. This paper presents an in-depth empirical analysis of SSL-trained representations, encompassing diverse models, architectures, and hyperparameters. Our study reveals an intriguing aspect of the SSL training process: it inherently facilitates the clustering of samples with respect to semantic labels, which is surprisingly driven by the SSL objective's regularization term. This clustering process not only enhances downstream classification but also compresses the data information. Furthermore, we establish that SSL-trained representations align more closely with semantic classes rather than random classes. Remarkably, we show that learned representations align with semantic classes across various hierarchical levels, and this alignment increases during training and when moving deeper into the network. Our findings provide valuable insights into SSL's representation learning mechanisms and their impact on performance across different sets of classes.

Numerical Methods For PDEs Over Manifolds Using Spectral Physics Informed Neural Networks

We introduce an approach for solving PDEs over manifolds using physics informed neural networks whose architecture aligns with spectral methods. The networks are trained to take in as input samples of an initial condition, a time stamp and point(s) on the manifold and then output the solution's value at the given time and point(s). We provide proofs of our method for the heat equation on the interval and examples of unique network architectures that are adapted to nonlinear equations on the sphere and the torus. We also show that our spectral-inspired neural network architectures outperform the standard physics informed architectures. Our extensive experimental results include generalization studies where the testing dataset of initial conditions is randomly sampled from a significantly larger space than the training set.

Exploring the Approximation Capabilities of Multiplicative Neural Networks for Smooth Functions

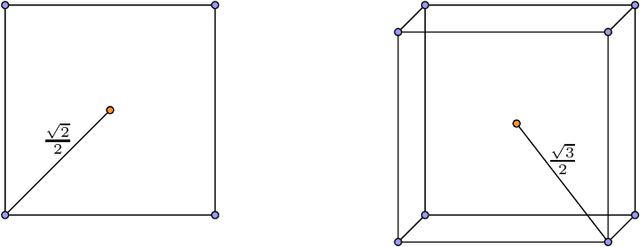
Multiplication layers are a key component in various influential neural network modules, including self-attention and hypernetwork layers. In this paper, we investigate the approximation capabilities of deep neural networks with intermediate neurons connected by simple multiplication operations. We consider two classes of target functions: generalized bandlimited functions, which are frequently used to model real-world signals with finite bandwidth, and Sobolev-Type balls, which are embedded in the Sobolev Space $\mathcal{W}^{r,2}$. Our results demonstrate that multiplicative neural networks can approximate these functions with significantly fewer layers and neurons compared to standard ReLU neural networks, with respect to both input dimension and approximation error. These findings suggest that multiplicative gates can outperform standard feed-forward layers and have potential for improving neural network design.

PR-DAD: Phase Retrieval Using Deep Auto-Decoders

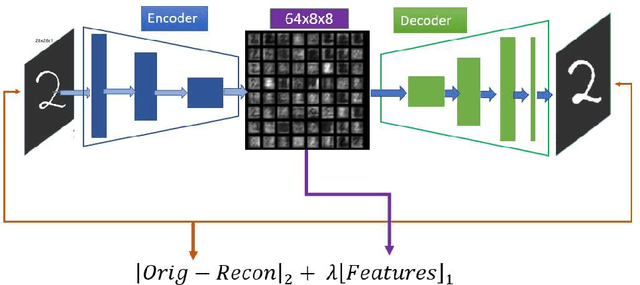
Phase retrieval is a well known ill-posed inverse problem where one tries to recover images given only the magnitude values of their Fourier transform as input. In recent years, new algorithms based on deep learning have been proposed, providing breakthrough results that surpass the results of the classical methods. In this work we provide a novel deep learning architecture PR-DAD (Phase Retrieval Using Deep Auto- Decoders), whose components are carefully designed based on mathematical modeling of the phase retrieval problem. The architecture provides experimental results that surpass all current results.

Nearest Class-Center Simplification through Intermediate Layers

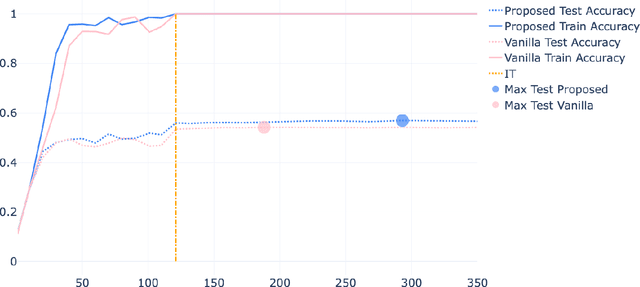
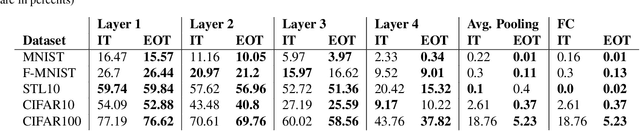
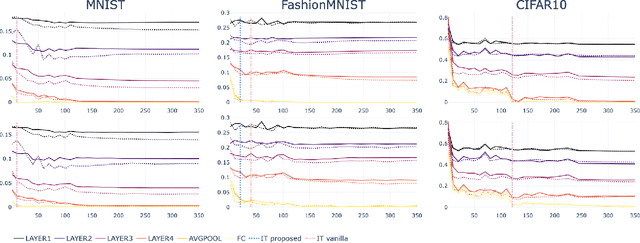
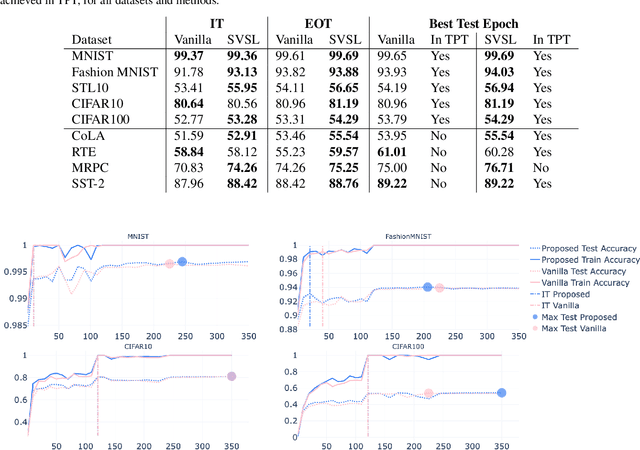
Recent advances in theoretical Deep Learning have introduced geometric properties that occur during training, past the Interpolation Threshold -- where the training error reaches zero. We inquire into the phenomena coined Neural Collapse in the intermediate layers of the networks, and emphasize the innerworkings of Nearest Class-Center Mismatch inside the deepnet. We further show that these processes occur both in vision and language model architectures. Lastly, we propose a Stochastic Variability-Simplification Loss (SVSL) that encourages better geometrical features in intermediate layers, and improves both train metrics and generalization.

Sparsity-Probe: Analysis tool for Deep Learning Models

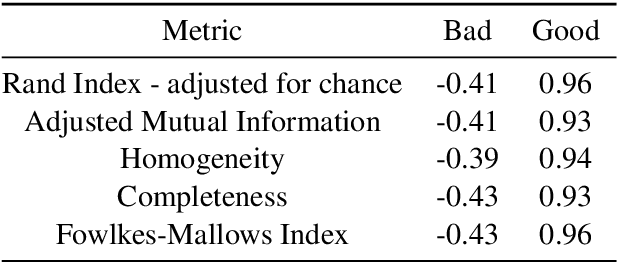
We propose a probe for the analysis of deep learning architectures that is based on machine learning and approximation theoretical principles. Given a deep learning architecture and a training set, during or after training, the Sparsity Probe allows to analyze the performance of intermediate layers by quantifying the geometrical features of representations of the training set. We show how the Sparsity Probe enables measuring the contribution of adding depth to a given architecture, to detect under-performing layers, etc., all this without any auxiliary test data set.

Wavelet Decomposition of Gradient Boosting

In this paper we introduce a significant improvement to the popular tree-based Stochastic Gradient Boosting algorithm using a wavelet decomposition of the trees. This approach is based on harmonic analysis and approximation theoretical elements, and as we show through extensive experimentation, our wavelet based method generally outperforms existing methods, particularly in difficult scenarios of class unbalance and mislabeling in the training data.

Function space analysis of deep learning representation layers

In this paper we propose a function space approach to Representation Learning and the analysis of the representation layers in deep learning architectures. We show how to compute a weak-type Besov smoothness index that quantifies the geometry of the clustering in the feature space. This approach was already applied successfully to improve the performance of machine learning algorithms such as the Random Forest and tree-based Gradient Boosting. Our experiments demonstrate that in well-known and well-performing trained networks, the Besov smoothness of the training set, measured in the corresponding hidden layer feature map representation, increases from layer to layer. We also contribute to the understanding of generalization by showing how the Besov smoothness of the representations, decreases as we add more mis-labeling to the training data. We hope this approach will contribute to the de-mystification of some aspects of deep learning.

Machine olfaction using time scattering of sensor multiresolution graphs

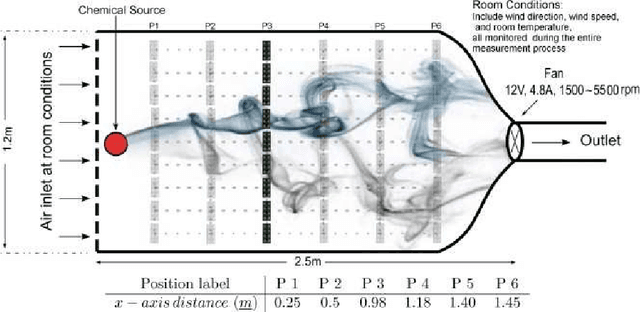
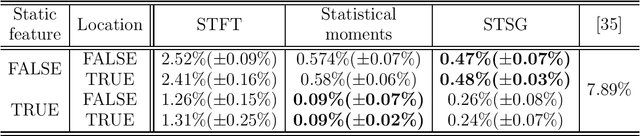
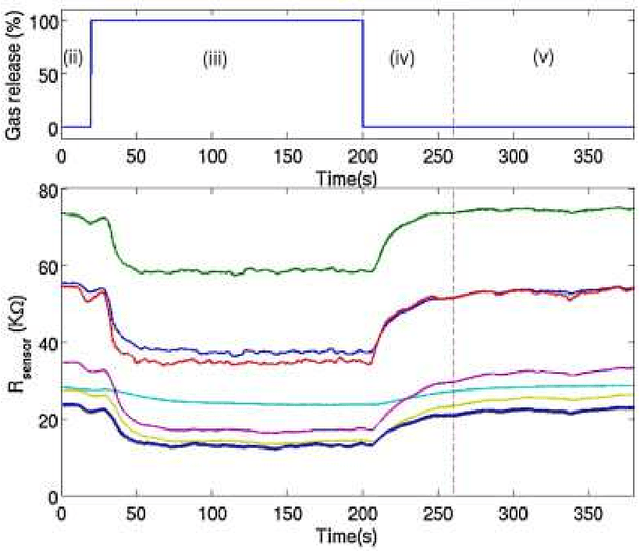
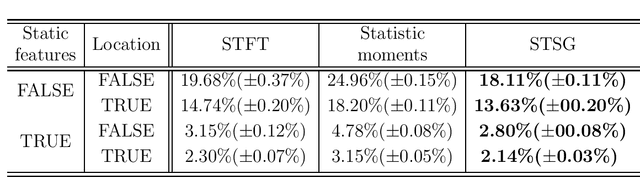
In this paper we construct a learning architecture for high dimensional time series sampled by sensor arrangements. Using a redundant wavelet decomposition on a graph constructed over the sensor locations, our algorithm is able to construct discriminative features that exploit the mutual information between the sensors. The algorithm then applies scattering networks to the time series graphs to create the feature space. We demonstrate our method on a machine olfaction problem, where one needs to classify the gas type and the location where it originates from data sampled by an array of sensors. Our experimental results clearly demonstrate that our method outperforms classical machine learning techniques used in previous studies.