Scene-based nonuniformity correction with homography transformation

Due to their affordable, low mass, and small dimensions, uncooled microbolometer-based thermal focal plane arrays (UC-FPAs) are useful for long-wave infrared (LWIR)imaging applications. However, in outdoor conditions typical in agricultural remote sensing, cameras based on UC-FPAs may suffer from drift in offset and gain. To tackle the persistent drift, the system requires continuous calibration. Our goal in this study was to eliminate this requirement via a computational schema. In a former study, we estimated unknown gain and offset values and thermographic images of an object from a sequence of pairs of successive images taken at two different blur levels.In the current work, we took on a similar problem using a sequence of shifted images, with relative shifts caused by realistic drone hovering modeled by homography transformation. This places our work in the realm of scene-based nonuniformity correction problems. We show that an object's thermographic values, as well as gain and offset, can be jointly estimated by relying on a few sets of shifted images. We use a minimum likelihood estimator, which is found using alternating minimization. Registration is done using a generalized Lucas-Kanade method. Simulations show promising accuracy with mean Pearson correlation of more than 0.9999998 between ground truth and restoration. Under ideal assumptions, this is equivalent to a mean restoration error of less than 0.01 Celsius degree.

End-to-end pipeline for simultaneous temperature estimation and super resolution of low-cost uncooled infrared camera frames for precision agriculture applications

Radiometric infrared (IR) imaging is a valuable technique for remote-sensing applications in precision agriculture, such as irrigation monitoring, crop health assessment, and yield estimation. Low-cost uncooled non-radiometric IR cameras offer new implementations in agricultural monitoring. However, these cameras have inherent drawbacks that limit their usability, such as low spatial resolution, spatially variant nonuniformity, and lack of radiometric calibration. In this article, we present an end-to-end pipeline for temperature estimation and super resolution of frames captured by a low-cost uncooled IR camera. The pipeline consists of two main components: a deep-learning-based temperature-estimation module, and a deep-learning-based super-resolution module. The temperature-estimation module learns to map the raw gray level IR images to the corresponding temperature maps while also correcting for nonuniformity. The super-resolution module uses a deep-learning network to enhance the spatial resolution of the IR images by scale factors of x2 and x4. We evaluated the performance of the pipeline on both simulated and real-world agricultural datasets composing of roughly 20,000 frames of various crops. For the simulated data, the results were on par with the real-world data with sub-degree accuracy. For the real data, the proposed pipeline was compared to a high-end radiometric thermal camera, and achieved sub-degree accuracy. The results of the real data are on par with the simulated data. The proposed pipeline can enable various applications in precision agriculture that require high quality thermal information from low-cost IR cameras.

Level Set KSVD

We present a new algorithm for image segmentation - Level-set KSVD. Level-set KSVD merges the methods of sparse dictionary learning for feature extraction and variational level-set method for image segmentation. Specifically, we use a generalization of the Chan-Vese functional with features learned by KSVD. The motivation for this model is agriculture based. Aerial images are taken in order to detect the spread of fungi in various crops. Our model is tested on such images of cotton fields. The results are compared to other methods.

Simultaneous temperature estimation and nonuniformity correction from multiple frames

Infrared (IR) cameras are widely used for temperature measurements in various applications, including agriculture, medicine, and security. Low-cost IR camera have an immense potential to replace expansive radiometric cameras in these applications, however low-cost microbolometer-based IR cameras are prone to spatially-variant nonuniformity and to drift in temperature measurements, which limits their usability in practical scenarios. To address these limitations, we propose a novel approach for simultaneous temperature estimation and nonuniformity correction from multiple frames captured by low-cost microbolometer-based IR cameras. We leverage the physical image acquisition model of the camera and incorporate it into a deep learning architecture called kernel estimation networks (KPN), which enables us to combine multiple frames despite imperfect registration between them. We also propose a novel offset block that incorporates the ambient temperature into the model and enables us to estimate the offset of the camera, which is a key factor in temperature estimation. Our findings demonstrate that the number of frames has a significant impact on the accuracy of temperature estimation and nonuniformity correction. Moreover, our approach achieves a significant improvement in performance compared to vanilla KPN, thanks to the offset block. The method was tested on real data collected by a low-cost IR camera mounted on a UAV, showing only a small average error of $0.27^\circ C-0.54^\circ C$ relative to costly scientific-grade radiometric cameras. Our method provides an accurate and efficient solution for simultaneous temperature estimation and nonuniformity correction, which has important implications for a wide range of practical applications.

Improving temperature estimation in low-cost infrared cameras using deep neural networks

Low-cost thermal cameras are inaccurate (usually $\pm 3^\circ C$) and have space-variant nonuniformity across their detector. Both inaccuracy and nonuniformity are dependent on the ambient temperature of the camera. The main goal of this work was to improve the temperature accuracy of low-cost cameras and rectify the nonuniformity. A nonuniformity simulator that accounts for the ambient temperature was developed. An end-to-end neural network that incorporates the ambient temperature at image acquisition was introduced. The neural network was trained with the simulated nonuniformity data to estimate the object's temperature and correct the nonuniformity, using only a single image and the ambient temperature measured by the camera itself. Results show that the proposed method lowered the mean temperature error by approximately $1^\circ C$ compared to previous works. In addition, applying a physical constraint on the network lowered the error by an additional $4\%$. The mean temperature error over an extensive validation dataset was $0.37^\circ C$. The method was verified on real data in the field and produced equivalent results.

A note on the variation of geometric functionals

Calculus of Variation combined with Differential Geometry as tools of modelling and solving problems in image processing and computer vision were introduced in the late 80's and the 90s of the 20th century. The beginning of an extensive work in these directions was marked by works such as Geodesic Active Contours (GAC), the Beltrami framework, level set method of Osher and Sethian the works of Charpiat et al. and the works by Chan and Vese to name just a few. In many cases the optimization of these functional are done by the gradient descent method via the calculation of the Euler-Lagrange equations. Straightforward use of the resulted EL equations in the gradient descent scheme leads to non-geometric and in some cases non sensical equations. It is costumary to modify these EL equations or even the functional itself in order to obtain geometric and/or sensical equations. The aim of this note is to point to the correct way to derive the EL and the gradient descent equations such that the resulted gradient descent equation is geometric and makes sense.

Solving the functional Eigen-Problem using Neural Networks

In this work, we explore the ability of NN (Neural Networks) to serve as a tool for finding eigen-pairs of ordinary differential equations. The question we aime to address is whether, given a self-adjoint operator, we can learn what are the eigenfunctions, and their matching eigenvalues. The topic of solving the eigen-problem is widely discussed in Image Processing, as many image processing algorithms can be thought of as such operators. We suggest an alternative to numeric methods of finding eigenpairs, which may potentially be more robust and have the ability to solve more complex problems. In this work, we focus on simple problems for which the analytical solution is known. This way, we are able to make initial steps in discovering the capabilities and shortcomings of DNN (Deep Neural Networks) in the given setting.

Unsupervised Deep Learning Algorithm for PDE-based Forward and Inverse Problems

We propose a neural network-based algorithm for solving forward and inverse problems for partial differential equations in unsupervised fashion. The solution is approximated by a deep neural network which is the minimizer of a cost function, and satisfies the PDE, boundary conditions, and additional regularizations. The method is mesh free and can be easily applied to an arbitrary regular domain. We focus on 2D second order elliptical system with non-constant coefficients, with application to Electrical Impedance Tomography.

Affine-invariant geodesic geometry of deformable 3D shapes

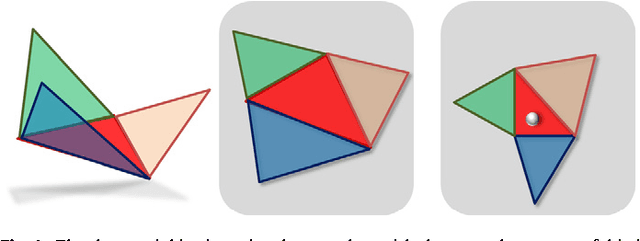
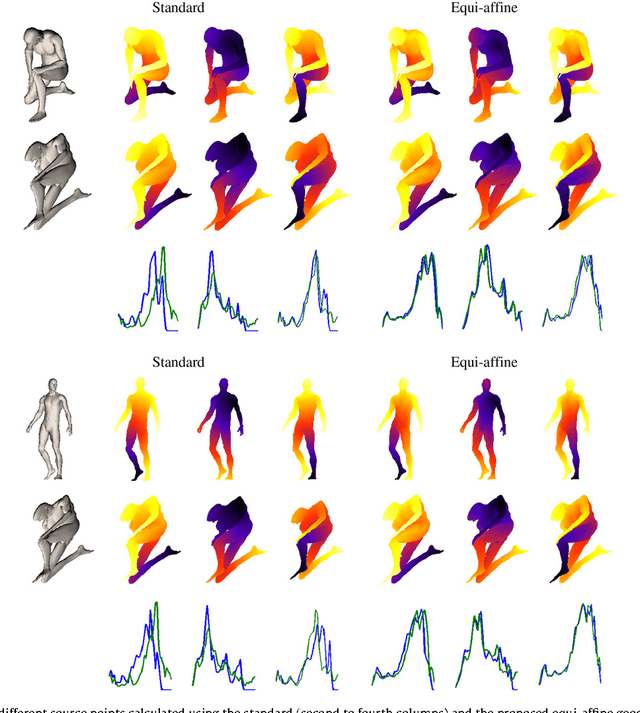
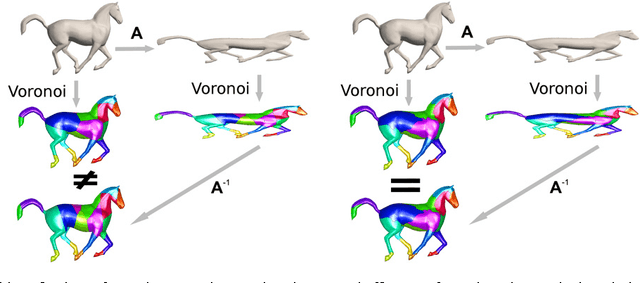
Natural objects can be subject to various transformations yet still preserve properties that we refer to as invariants. Here, we use definitions of affine invariant arclength for surfaces in R^3 in order to extend the set of existing non-rigid shape analysis tools. In fact, we show that by re-defining the surface metric as its equi-affine version, the surface with its modified metric tensor can be treated as a canonical Euclidean object on which most classical Euclidean processing and analysis tools can be applied. The new definition of a metric is used to extend the fast marching method technique for computing geodesic distances on surfaces, where now, the distances are defined with respect to an affine invariant arclength. Applications of the proposed framework demonstrate its invariance, efficiency, and accuracy in shape analysis.

Affine-invariant diffusion geometry for the analysis of deformable 3D shapes

We introduce an (equi-)affine invariant diffusion geometry by which surfaces that go through squeeze and shear transformations can still be properly analyzed. The definition of an affine invariant metric enables us to construct an invariant Laplacian from which local and global geometric structures are extracted. Applications of the proposed framework demonstrate its power in generalizing and enriching the existing set of tools for shape analysis.