NICE: Noise Injection and Clamping Estimation for Neural Network Quantization

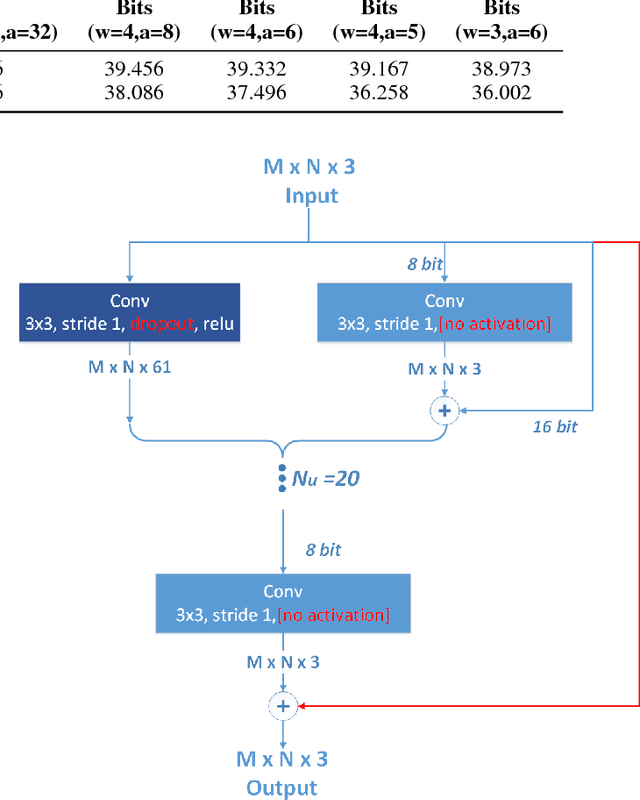
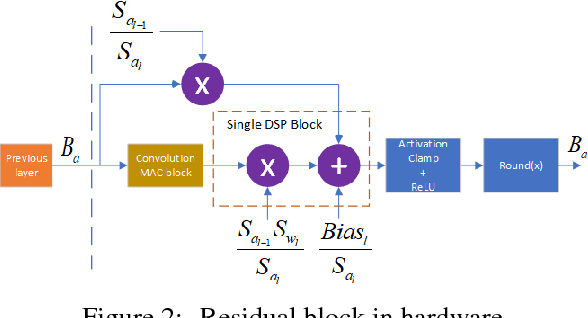
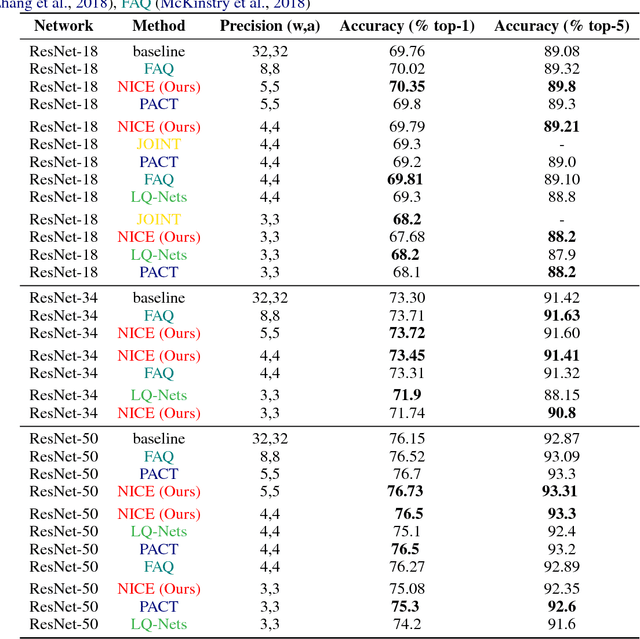
Convolutional Neural Networks (CNN) are very popular in many fields including computer vision, speech recognition, natural language processing, to name a few. Though deep learning leads to groundbreaking performance in these domains, the networks used are very demanding computationally and are far from real-time even on a GPU, which is not power efficient and therefore does not suit low power systems such as mobile devices. To overcome this challenge, some solutions have been proposed for quantizing the weights and activations of these networks, which accelerate the runtime significantly. Yet, this acceleration comes at the cost of a larger error. The \uniqname method proposed in this work trains quantized neural networks by noise injection and a learned clamping, which improve the accuracy. This leads to state-of-the-art results on various regression and classification tasks, e.g., ImageNet classification with architectures such as ResNet-18/34/50 with low as 3-bit weights and activations. We implement the proposed solution on an FPGA to demonstrate its applicability for low power real-time applications. The implementation of the paper is available at https://github.com/Lancer555/NICE

Multimodal diffusion geometry by joint diagonalization of Laplacians

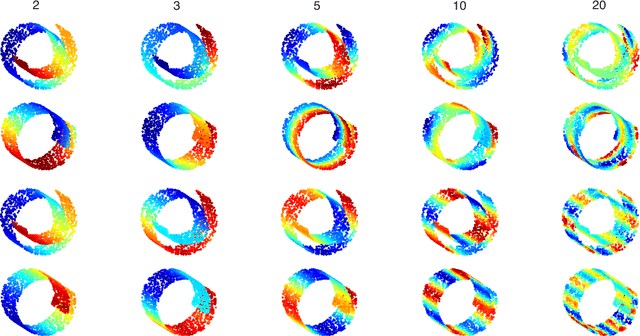
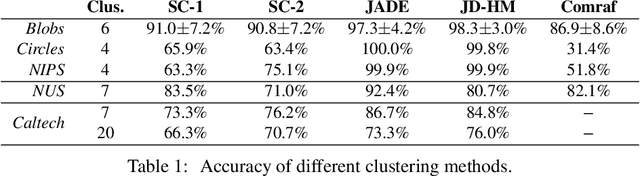
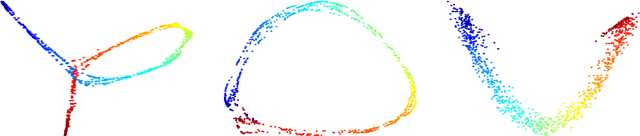
We construct an extension of diffusion geometry to multiple modalities through joint approximate diagonalization of Laplacian matrices. This naturally extends classical data analysis tools based on spectral geometry, such as diffusion maps and spectral clustering. We provide several synthetic and real examples of manifold learning, retrieval, and clustering demonstrating that the joint diffusion geometry frequently better captures the inherent structure of multi-modal data. We also show that many previous attempts to construct multimodal spectral clustering can be seen as particular cases of joint approximate diagonalization of the Laplacians.

Spectral descriptors for deformable shapes

Informative and discriminative feature descriptors play a fundamental role in deformable shape analysis. For example, they have been successfully employed in correspondence, registration, and retrieval tasks. In the recent years, significant attention has been devoted to descriptors obtained from the spectral decomposition of the Laplace-Beltrami operator associated with the shape. Notable examples in this family are the heat kernel signature (HKS) and the wave kernel signature (WKS). Laplacian-based descriptors achieve state-of-the-art performance in numerous shape analysis tasks; they are computationally efficient, isometry-invariant by construction, and can gracefully cope with a variety of transformations. In this paper, we formulate a generic family of parametric spectral descriptors. We argue that in order to be optimal for a specific task, the descriptor should take into account the statistics of the corpus of shapes to which it is applied (the "signal") and those of the class of transformations to which it is made insensitive (the "noise"). While such statistics are hard to model axiomatically, they can be learned from examples. Following the spirit of the Wiener filter in signal processing, we show a learning scheme for the construction of optimal spectral descriptors and relate it to Mahalanobis metric learning. The superiority of the proposed approach is demonstrated on the SHREC'10 benchmark.

A correspondence-less approach to matching of deformable shapes

Finding a match between partially available deformable shapes is a challenging problem with numerous applications. The problem is usually approached by computing local descriptors on a pair of shapes and then establishing a point-wise correspondence between the two. In this paper, we introduce an alternative correspondence-less approach to matching fragments to an entire shape undergoing a non-rigid deformation. We use diffusion geometric descriptors and optimize over the integration domains on which the integral descriptors of the two parts match. The problem is regularized using the Mumford-Shah functional. We show an efficient discretization based on the Ambrosio-Tortorelli approximation generalized to triangular meshes. Experiments demonstrating the success of the proposed method are presented.

Diffusion framework for geometric and photometric data fusion in non-rigid shape analysis

In this paper, we explore the use of the diffusion geometry framework for the fusion of geometric and photometric information in local and global shape descriptors. Our construction is based on the definition of a diffusion process on the shape manifold embedded into a high-dimensional space where the embedding coordinates represent the photometric information. Experimental results show that such data fusion is useful in coping with different challenges of shape analysis where pure geometric and pure photometric methods fail.

Affine-invariant geodesic geometry of deformable 3D shapes

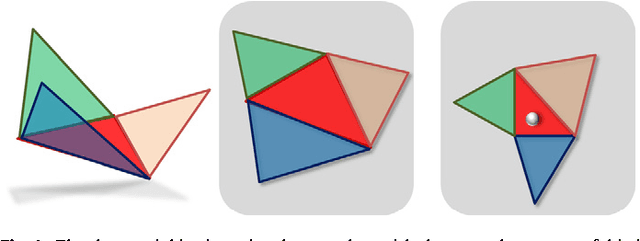
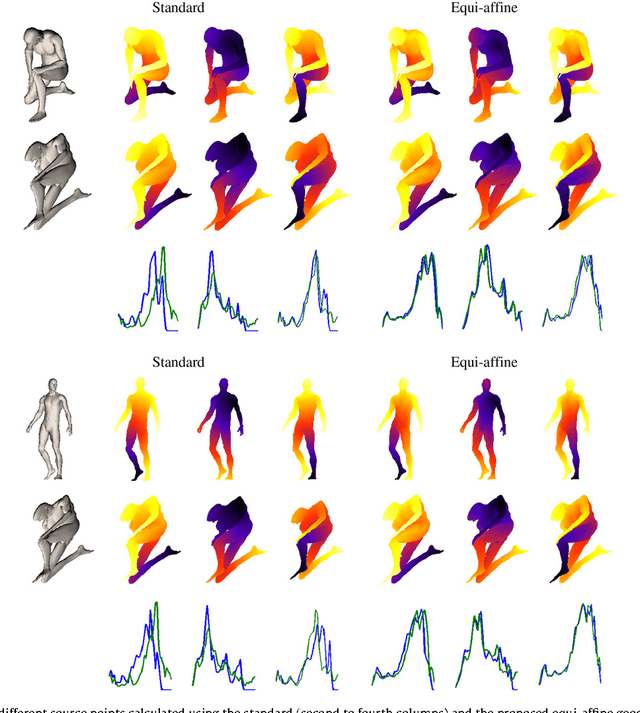
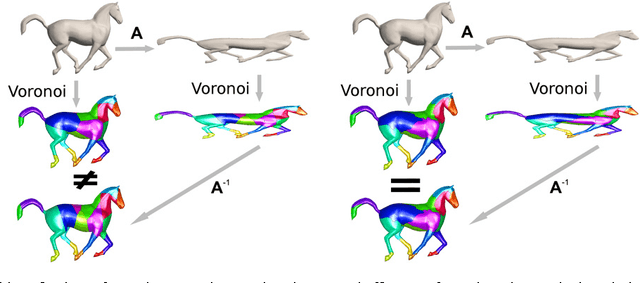
Natural objects can be subject to various transformations yet still preserve properties that we refer to as invariants. Here, we use definitions of affine invariant arclength for surfaces in R^3 in order to extend the set of existing non-rigid shape analysis tools. In fact, we show that by re-defining the surface metric as its equi-affine version, the surface with its modified metric tensor can be treated as a canonical Euclidean object on which most classical Euclidean processing and analysis tools can be applied. The new definition of a metric is used to extend the fast marching method technique for computing geodesic distances on surfaces, where now, the distances are defined with respect to an affine invariant arclength. Applications of the proposed framework demonstrate its invariance, efficiency, and accuracy in shape analysis.

Affine-invariant diffusion geometry for the analysis of deformable 3D shapes

We introduce an (equi-)affine invariant diffusion geometry by which surfaces that go through squeeze and shear transformations can still be properly analyzed. The definition of an affine invariant metric enables us to construct an invariant Laplacian from which local and global geometric structures are extracted. Applications of the proposed framework demonstrate its power in generalizing and enriching the existing set of tools for shape analysis.

The Video Genome

Fast evolution of Internet technologies has led to an explosive growth of video data available in the public domain and created unprecedented challenges in the analysis, organization, management, and control of such content. The problems encountered in video analysis such as identifying a video in a large database (e.g. detecting pirated content in YouTube), putting together video fragments, finding similarities and common ancestry between different versions of a video, have analogous counterpart problems in genetic research and analysis of DNA and protein sequences. In this paper, we exploit the analogy between genetic sequences and videos and propose an approach to video analysis motivated by genomic research. Representing video information as video DNA sequences and applying bioinformatic algorithms allows to search, match, and compare videos in large-scale databases. We show an application for content-based metadata mapping between versions of annotated video.