Functional correspondence by matrix completion

In this paper, we consider the problem of finding dense intrinsic correspondence between manifolds using the recently introduced functional framework. We pose the functional correspondence problem as matrix completion with manifold geometric structure and inducing functional localization with the $L_1$ norm. We discuss efficient numerical procedures for the solution of our problem. Our method compares favorably to the accuracy of state-of-the-art correspondence algorithms on non-rigid shape matching benchmarks, and is especially advantageous in settings when only scarce data is available.

Structure-preserving color transformations using Laplacian commutativity

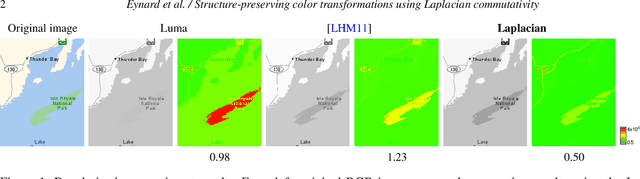
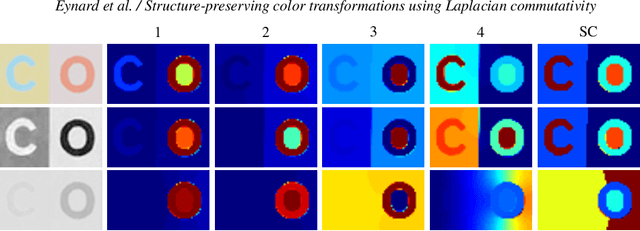
Mappings between color spaces are ubiquitous in image processing problems such as gamut mapping, decolorization, and image optimization for color-blind people. Simple color transformations often result in information loss and ambiguities (for example, when mapping from RGB to grayscale), and one wishes to find an image-specific transformation that would preserve as much as possible the structure of the original image in the target color space. In this paper, we propose Laplacian colormaps, a generic framework for structure-preserving color transformations between images. We use the image Laplacian to capture the structural information, and show that if the color transformation between two images preserves the structure, the respective Laplacians have similar eigenvectors, or in other words, are approximately jointly diagonalizable. Employing the relation between joint diagonalizability and commutativity of matrices, we use Laplacians commutativity as a criterion of color mapping quality and minimize it w.r.t. the parameters of a color transformation to achieve optimal structure preservation. We show numerous applications of our approach, including color-to-gray conversion, gamut mapping, multispectral image fusion, and image optimization for color deficient viewers.

Diffusion framework for geometric and photometric data fusion in non-rigid shape analysis

In this paper, we explore the use of the diffusion geometry framework for the fusion of geometric and photometric information in local and global shape descriptors. Our construction is based on the definition of a diffusion process on the shape manifold embedded into a high-dimensional space where the embedding coordinates represent the photometric information. Experimental results show that such data fusion is useful in coping with different challenges of shape analysis where pure geometric and pure photometric methods fail.