E Pluribus Unum: Guidelines on Multi-Objective Evaluation of Recommender Systems

Recommender Systems today are still mostly evaluated in terms of accuracy, with other aspects beyond the immediate relevance of recommendations, such as diversity, long-term user retention and fairness, often taking a back seat. Moreover, reconciling multiple performance perspectives is by definition indeterminate, presenting a stumbling block to those in the pursuit of rounded evaluation of Recommender Systems. EvalRS 2022 -- a data challenge designed around Multi-Objective Evaluation -- was a first practical endeavour, providing many insights into the requirements and challenges of balancing multiple objectives in evaluation. In this work, we reflect on EvalRS 2022 and expound upon crucial learnings to formulate a first-principles approach toward Multi-Objective model selection, and outline a set of guidelines for carrying out a Multi-Objective Evaluation challenge, with potential applicability to the problem of rounded evaluation of competing models in real-world deployments.

EvalRS 2023. Well-Rounded Recommender Systems For Real-World Deployments

EvalRS aims to bring together practitioners from industry and academia to foster a debate on rounded evaluation of recommender systems, with a focus on real-world impact across a multitude of deployment scenarios. Recommender systems are often evaluated only through accuracy metrics, which fall short of fully characterizing their generalization capabilities and miss important aspects, such as fairness, bias, usefulness, informativeness. This workshop builds on the success of last year's workshop at CIKM, but with a broader scope and an interactive format.

Beltrami Flow and Neural Diffusion on Graphs

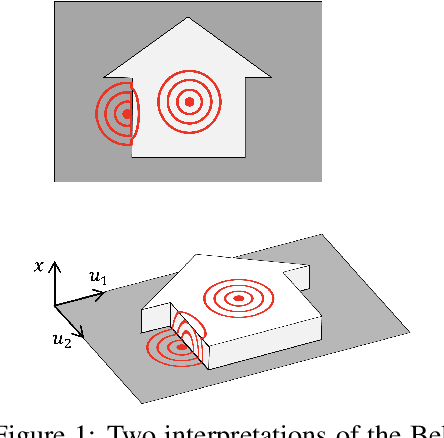
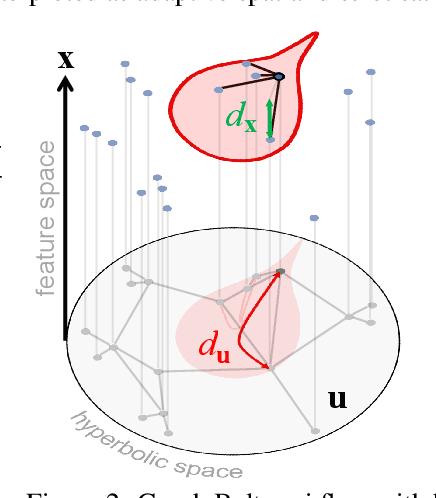
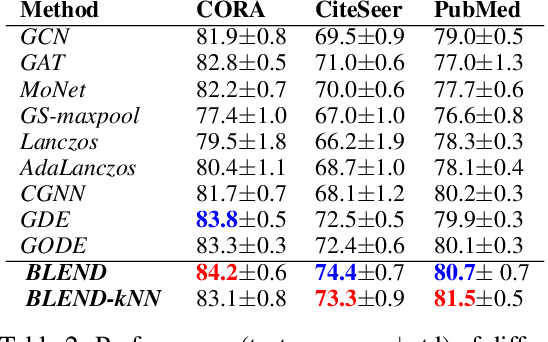
We propose a novel class of graph neural networks based on the discretised Beltrami flow, a non-Euclidean diffusion PDE. In our model, node features are supplemented with positional encodings derived from the graph topology and jointly evolved by the Beltrami flow, producing simultaneously continuous feature learning and topology evolution. The resulting model generalises many popular graph neural networks and achieves state-of-the-art results on several benchmarks.

Temporal Graph Networks for Deep Learning on Dynamic Graphs

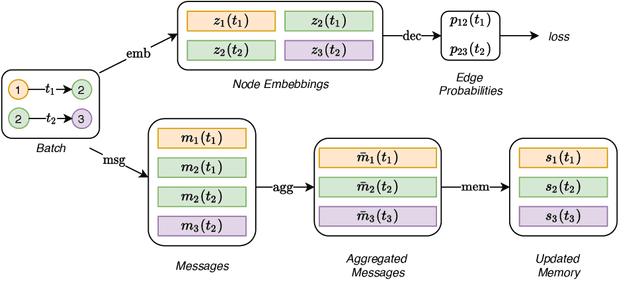
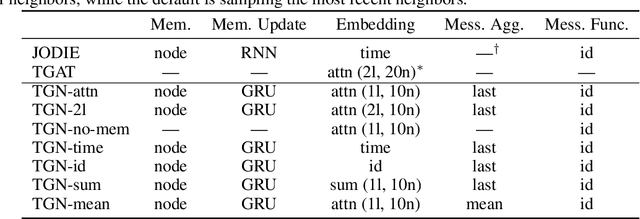
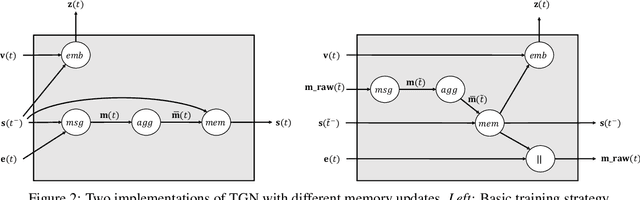
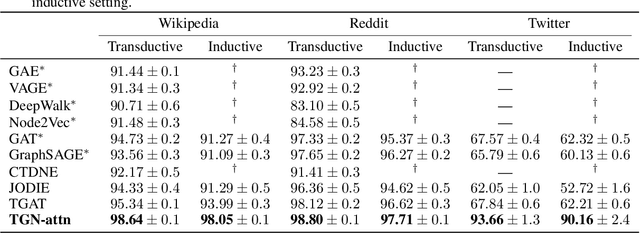
Graph Neural Networks (GNNs) have recently become increasingly popular due to their ability to learn complex systems of relations or interactions arising in a broad spectrum of problems ranging from biology and particle physics to social networks and recommendation systems. Despite the plethora of different models for deep learning on graphs, few approaches have been proposed thus far for dealing with graphs that present some sort of dynamic nature (e.g. evolving features or connectivity over time). In this paper, we present Temporal Graph Networks (TGNs), a generic, efficient framework for deep learning on dynamic graphs represented as sequences of timed events. Thanks to a novel combination of memory modules and graph-based operators, TGNs are able to significantly outperform previous approaches being at the same time more computationally efficient. We furthermore show that several previous models for learning on dynamic graphs can be cast as specific instances of our framework. We perform a detailed ablation study of different components of our framework and devise the best configuration that achieves state-of-the-art performance on several transductive and inductive prediction tasks for dynamic graphs.

SIGN: Scalable Inception Graph Neural Networks

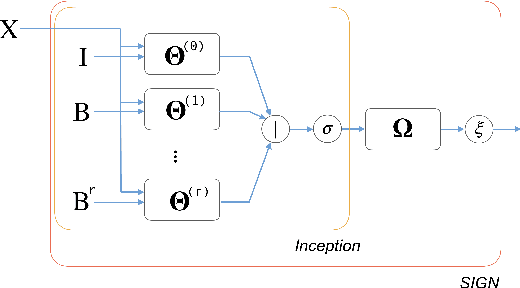
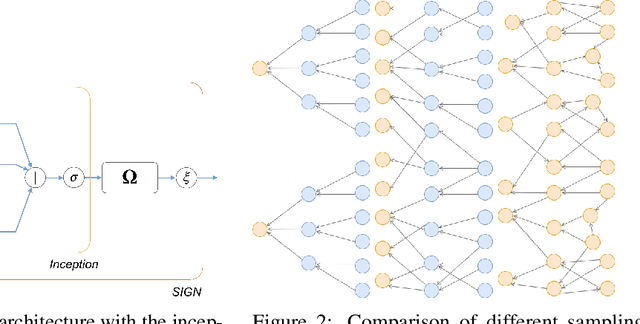
Geometric deep learning, a novel class of machine learning algorithms extending classical deep learning architectures to non-Euclidean structured data such as manifolds and graphs, has recently been applied to a broad spectrum of problems ranging from computer graphics and chemistry to high energy physics and social media. In this paper, we propose SIGN, a scalable graph neural network analogous to the popular inception module used in classical convolutional architectures. We show that our architecture is able to effectively deal with large-scale graphs via pre-computed multi-scale neighborhood features. Extensive experimental evaluation on various open benchmarks shows the competitive performance of our approach compared to a variety of popular architectures, while requiring a fraction of training and inference time.

Fake News Detection on Social Media using Geometric Deep Learning

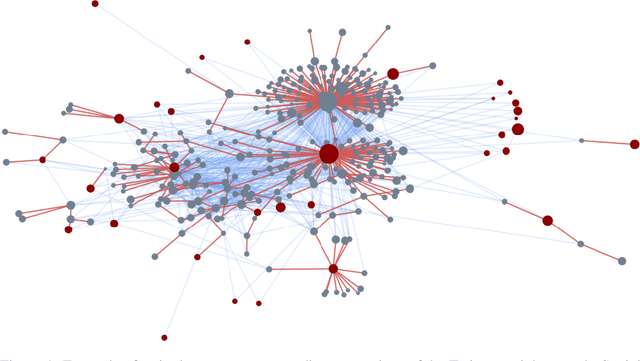
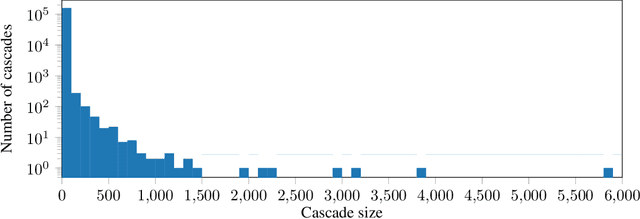
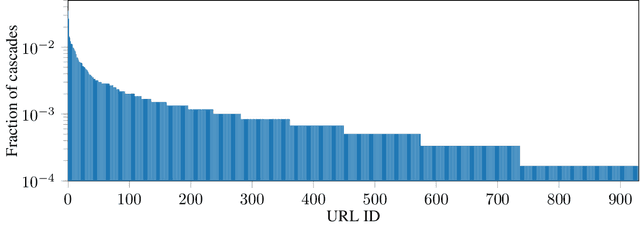
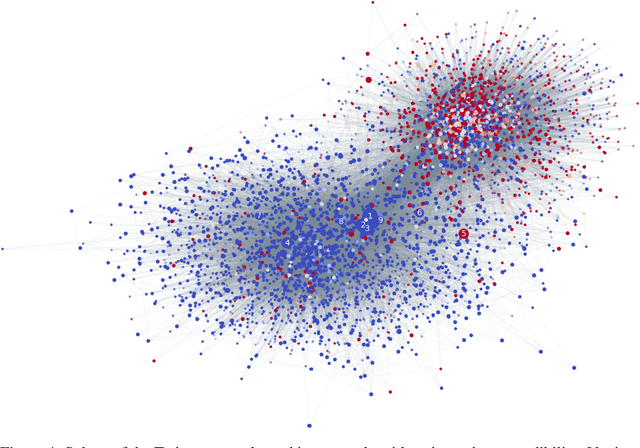
Social media are nowadays one of the main news sources for millions of people around the globe due to their low cost, easy access and rapid dissemination. This however comes at the cost of dubious trustworthiness and significant risk of exposure to 'fake news', intentionally written to mislead the readers. Automatically detecting fake news poses challenges that defy existing content-based analysis approaches. One of the main reasons is that often the interpretation of the news requires the knowledge of political or social context or 'common sense', which current NLP algorithms are still missing. Recent studies have shown that fake and real news spread differently on social media, forming propagation patterns that could be harnessed for the automatic fake news detection. Propagation-based approaches have multiple advantages compared to their content-based counterparts, among which is language independence and better resilience to adversarial attacks. In this paper we show a novel automatic fake news detection model based on geometric deep learning. The underlying core algorithms are a generalization of classical CNNs to graphs, allowing the fusion of heterogeneous data such as content, user profile and activity, social graph, and news propagation. Our model was trained and tested on news stories, verified by professional fact-checking organizations, that were spread on Twitter. Our experiments indicate that social network structure and propagation are important features allowing highly accurate (92.7% ROC AUC) fake news detection. Second, we observe that fake news can be reliably detected at an early stage, after just a few hours of propagation. Third, we test the aging of our model on training and testing data separated in time. Our results point to the promise of propagation-based approaches for fake news detection as an alternative or complementary strategy to content-based approaches.

Shape-from-intrinsic operator

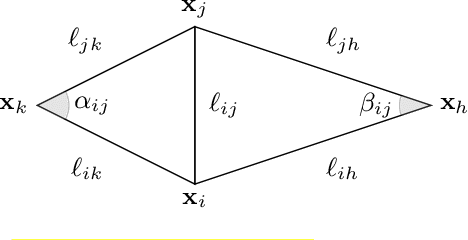
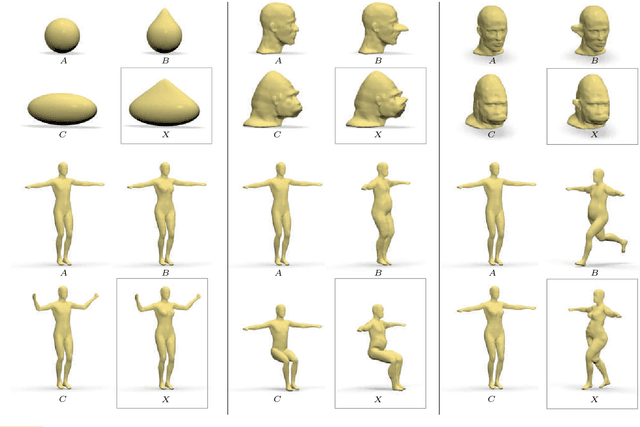
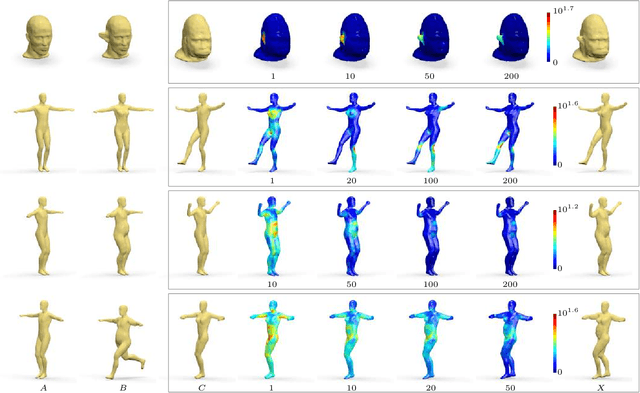
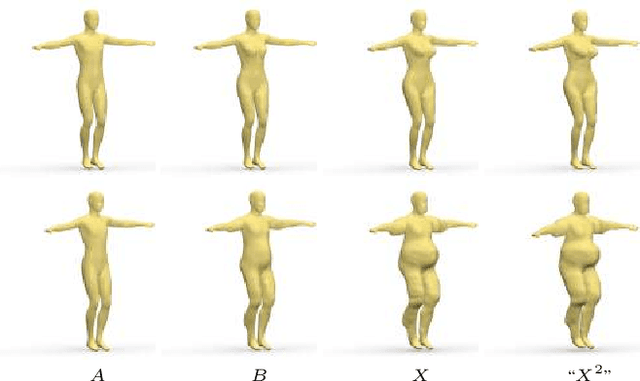
Shape-from-X is an important class of problems in the fields of geometry processing, computer graphics, and vision, attempting to recover the structure of a shape from some observations. In this paper, we formulate the problem of shape-from-operator (SfO), recovering an embedding of a mesh from intrinsic differential operators defined on the mesh. Particularly interesting instances of our SfO problem include synthesis of shape analogies, shape-from-Laplacian reconstruction, and shape exaggeration. Numerically, we approach the SfO problem by splitting it into two optimization sub-problems that are applied in an alternating scheme: metric-from-operator (reconstruction of the discrete metric from the intrinsic operator) and embedding-from-metric (finding a shape embedding that would realize a given metric, a setting of the multidimensional scaling problem).

Structure-preserving color transformations using Laplacian commutativity

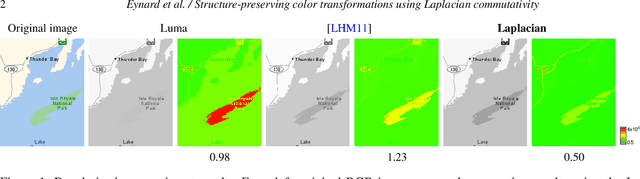
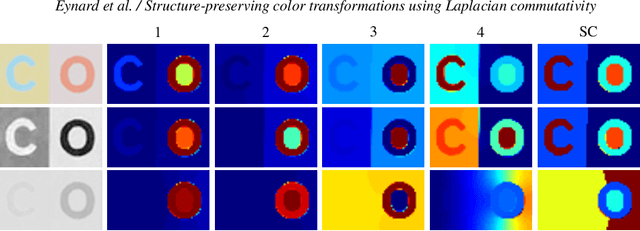
Mappings between color spaces are ubiquitous in image processing problems such as gamut mapping, decolorization, and image optimization for color-blind people. Simple color transformations often result in information loss and ambiguities (for example, when mapping from RGB to grayscale), and one wishes to find an image-specific transformation that would preserve as much as possible the structure of the original image in the target color space. In this paper, we propose Laplacian colormaps, a generic framework for structure-preserving color transformations between images. We use the image Laplacian to capture the structural information, and show that if the color transformation between two images preserves the structure, the respective Laplacians have similar eigenvectors, or in other words, are approximately jointly diagonalizable. Employing the relation between joint diagonalizability and commutativity of matrices, we use Laplacians commutativity as a criterion of color mapping quality and minimize it w.r.t. the parameters of a color transformation to achieve optimal structure preservation. We show numerous applications of our approach, including color-to-gray conversion, gamut mapping, multispectral image fusion, and image optimization for color deficient viewers.

Multimodal diffusion geometry by joint diagonalization of Laplacians

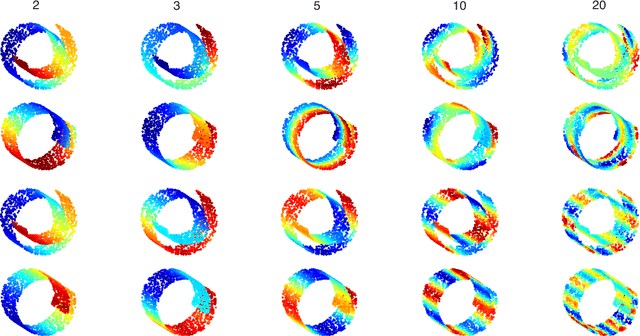
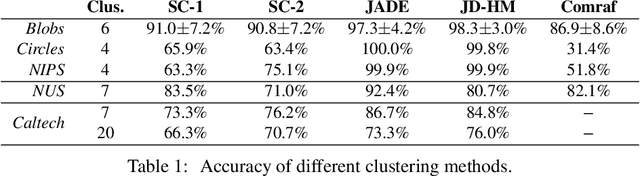
We construct an extension of diffusion geometry to multiple modalities through joint approximate diagonalization of Laplacian matrices. This naturally extends classical data analysis tools based on spectral geometry, such as diffusion maps and spectral clustering. We provide several synthetic and real examples of manifold learning, retrieval, and clustering demonstrating that the joint diffusion geometry frequently better captures the inherent structure of multi-modal data. We also show that many previous attempts to construct multimodal spectral clustering can be seen as particular cases of joint approximate diagonalization of the Laplacians.