Learning Visual-Semantic Subspace Representations for Propositional Reasoning

Learning representations that capture rich semantic relationships and accommodate propositional calculus poses a significant challenge. Existing approaches are either contrastive, lacking theoretical guarantees, or fall short in effectively representing the partial orders inherent to rich visual-semantic hierarchies. In this paper, we propose a novel approach for learning visual representations that not only conform to a specified semantic structure but also facilitate probabilistic propositional reasoning. Our approach is based on a new nuclear norm-based loss. We show that its minimum encodes the spectral geometry of the semantics in a subspace lattice, where logical propositions can be represented by projection operators.

Hyperbolic vs Euclidean Embeddings in Few-Shot Learning: Two Sides of the Same Coin

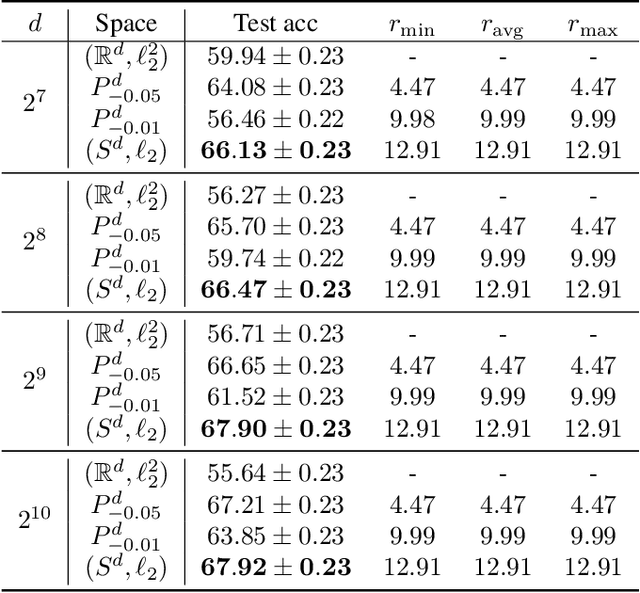
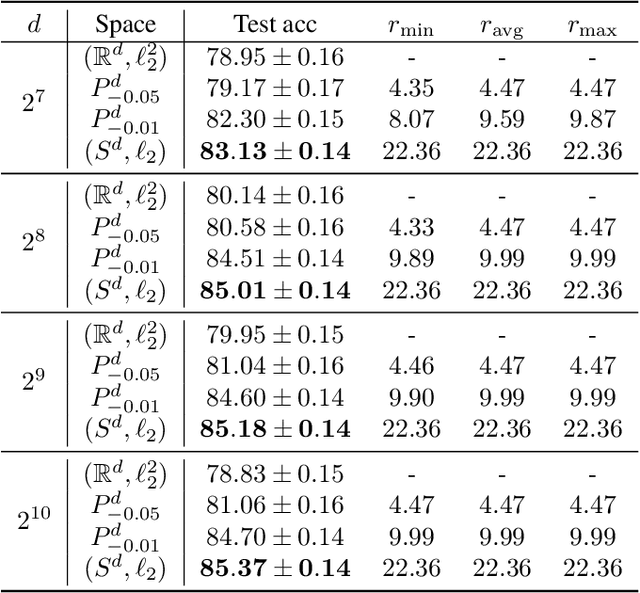
Recent research in representation learning has shown that hierarchical data lends itself to low-dimensional and highly informative representations in hyperbolic space. However, even if hyperbolic embeddings have gathered attention in image recognition, their optimization is prone to numerical hurdles. Further, it remains unclear which applications stand to benefit the most from the implicit bias imposed by hyperbolicity, when compared to traditional Euclidean features. In this paper, we focus on prototypical hyperbolic neural networks. In particular, the tendency of hyperbolic embeddings to converge to the boundary of the Poincar\'e ball in high dimensions and the effect this has on few-shot classification. We show that the best few-shot results are attained for hyperbolic embeddings at a common hyperbolic radius. In contrast to prior benchmark results, we demonstrate that better performance can be achieved by a fixed-radius encoder equipped with the Euclidean metric, regardless of the embedding dimension.

EvalRS 2023. Well-Rounded Recommender Systems For Real-World Deployments

EvalRS aims to bring together practitioners from industry and academia to foster a debate on rounded evaluation of recommender systems, with a focus on real-world impact across a multitude of deployment scenarios. Recommender systems are often evaluated only through accuracy metrics, which fall short of fully characterizing their generalization capabilities and miss important aspects, such as fairness, bias, usefulness, informativeness. This workshop builds on the success of last year's workshop at CIKM, but with a broader scope and an interactive format.

Rotation Averaging in a Split Second: A Primal-Dual Method and a Closed-Form for Cycle Graphs

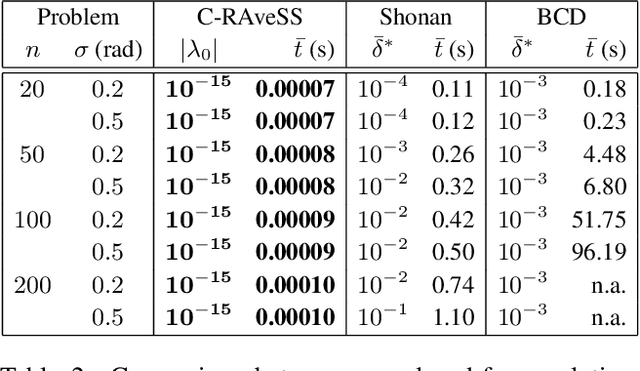
A cornerstone of geometric reconstruction, rotation averaging seeks the set of absolute rotations that optimally explains a set of measured relative orientations between them. In spite of being an integral part of bundle adjustment and structure-from-motion, averaging rotations is both a non-convex and high-dimensional optimization problem. In this paper, we address it from a maximum likelihood estimation standpoint and make a twofold contribution. Firstly, we set forth a novel initialization-free primal-dual method which we show empirically to converge to the global optimum. Further, we derive what is to our knowledge, the first optimal closed-form solution for rotation averaging in cycle graphs and contextualize this result within spectral graph theory. Our proposed methods achieve a significant gain both in precision and performance.